양자정보통신 기술동향

1982년 Richard Feynman[1]에 따르면 물리현상을 양자컴퓨터로 모사할 수 있는 가능성에 대해 언급하였고, 1985년 Deutsch[2]는 양자컴퓨터가 universal Tu-ring machine임을 밝히고 양자병렬성으로 고전 컴퓨터보다 빨리 연산이 가능함을 밝혔다. 1996년 MIT의 Seth Lloyd[3]도 양자컴퓨터의 가능성을 증명하여 양자역학을 물리학 실험실에서 나와 정보통신과 결합한 새로운 응용분야를 만들게 되었다. 일반적으로 정보통신은 통신과 컴퓨팅의 분야로 나눌 수 있고, 통신분야에서는 양자키 분배기술 등을 사용한 양자암호통신, 컴퓨팅 분야에서는 양자컴퓨터가 최종 결과물이 될 것이다. 양자암호통신은 물리적으로도 도청이 불가능한 암호통신을 가능하게 하여 1:1 통신에서는 적용 가능한 수준으로 개발되어 있으며, 양자컴퓨터는 현재의 컴퓨터가 오랜 시간을 걸려 어렵게 푸는 문제를 쉽고 빠르게 풀 수 있는 컴퓨터로, 현재로서는 구현 가능성을 보여주고 있는 단계이다. 최근 선진국과 중국 등에서 많은 투자가 이루어지고 있어서 조만간 실용 가능한 양자컴퓨터의 등장이 예견되고, D-Wave사의 양자컴퓨터가 2014년 2월 7일자 Time지의 표지기사로 소개[4]되었다.

본고에서는 양자정보통신의 기술 개념에 대해 설명하고 전 세계의 기술동향과 우리나라의 방향에 대해 설명하고자 한다.

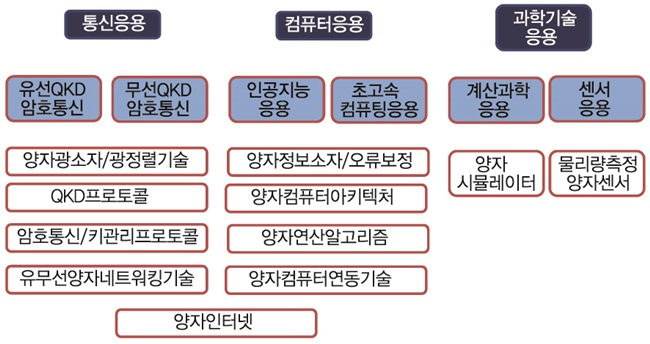
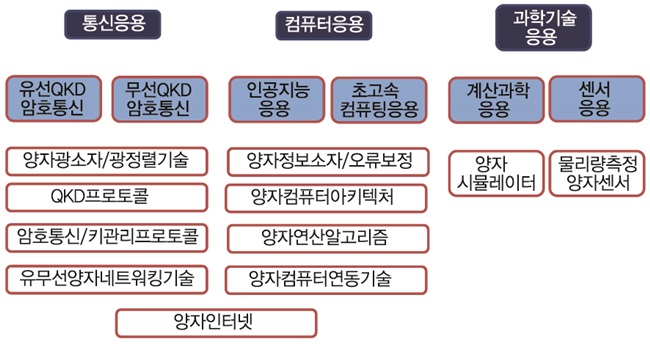
양자정보통신 기술은 궁극적으로 양자인터넷으로 발전하게 되겠지만 가능하게 할 기술은 양자역학의 정보통신 응용 측면에서 (그림 1)과 같이 분류해 볼 수 있다. 통신응용에서는 단일광자 또는 얽힘광자 등을 광섬유 또는 자유공간을 통한 양자키 분배기술로 키를 배분하고 이 키를 이용한 암호통신을 말하는 것으로 키 분배과정에서 물리적인 해킹에 대해서도 이론적으로는 무조건 안전(unconditionally safe)하다는 점이 증명되어 있다. 컴퓨터 응용에서는 고전 컴퓨터가 풀 수 없는 문제를 양자알고리즘 등으로 해결할 수 있도록 아키텍처, 소자 및 오류보정 등의 기술이 포함되어 있다. 과학기술 응용으로는 고전 컴퓨터로는 시뮬레이션이 불가능한 양자물리현상을 시뮬레이션이 가능하게 해 주며, 중력, 자기장, 시간, 전기장 등을 정밀하게 측정할 수 있는 정밀센서로의 응용도 가능하다.

(그림 1)

양자성질과 그 응용

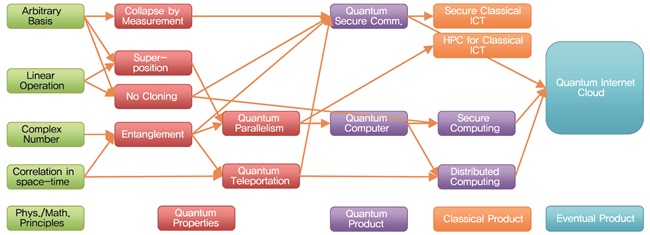
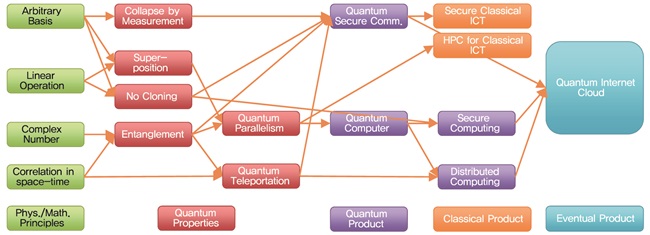
이용 가능한 양자역학적 상태 및 성질과 이를 응용한 응용분야간의 상관관계는 (그림 2)에 표시하였다.

(그림 2)

양자정보통신 기술분류

양자역학적 기본 성질에는 크게 3가지를 말하고 있는데, 중첩(Superposition), 얽힘(Entanglement), 관측붕괴(Collapse by Measurement)이다. 그 외의 성질이나 정리인 복사불가(No Cloning Theorem), 양자병별화(Parallelism), 원격이동(Teleportation)의 방법 등을 사용하여 양자암호통신, 양자컴퓨터를 만들 수 있게 된다. 양자정보통신 기술이 활성화될 때, 기존의 고전 컴퓨터의 보안성과 계산성의 보완도 이루어 질 것이며, 궁극적으로는 양자인터넷클라우드[5]가 만들어져서 모든 사람들이 양자컴퓨터의 기능을 알지 못하는 순간에도 사용할 수 있도록 발전할 것으로 생각된다.

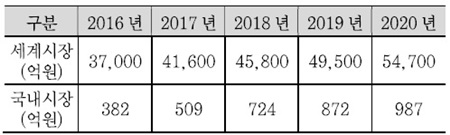
세계 양자정보통신 시장규모는 2015년 3.3조원에서 연평균 10.4%로 성장하여 2020년 5.5조원이 될 것으로 예측된다. 일반적으로 시장조사기관에서 Quantum Com-puting이란 표현으로 양자정보통신을 지칭하고 있으며 양자암호, 양자컴퓨터, 과학기술응용 등을 통칭하고 있다. <표 1>에 세계 양자정보통신 시장전망을 실었다.

<표 1>

양자정보통신 예상 시장규모

<출처>: 국내시장은 Market Research Media(2012). 자료를 이용하여 추정함.

1984년 Bennett과 Brassard는 단일광자를 사용한 암호분배 방법[6]을 제안하였고 1989년 실험적으로도 증명하여 양자키 분배(Quantum Key Distribution) 프로토콜인 BB84에 의한 암호통신이 가능하게 되었다. 양자암호통신은 멀리 떨어진 장소 간의 양자상태를 전송하는 것을 말하고 이러한 qubit을 사용한 통신은 양자컴퓨팅, 양자시뮬레이션 등에까지 널리 사용 가능한 기술로 현재 가장 많은 응용으로는 QKD를 이용한 암호통신이다. 향후 기술의 발전에 따라 여러 개의 양자시뮬레이터 또는 양자컴퓨터 노드 간의 양자상태 전송에도 사용 가능할 것으로 예상된다.

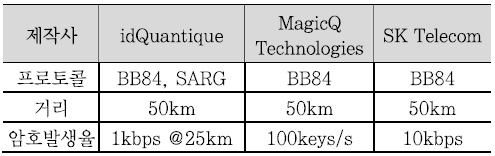
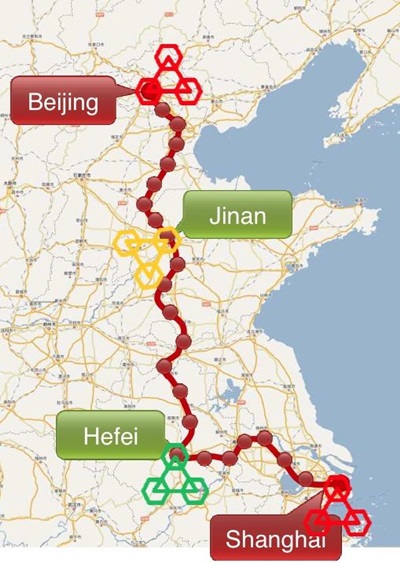
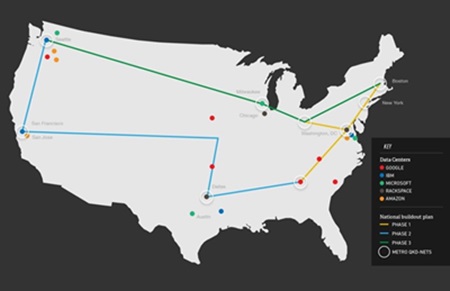
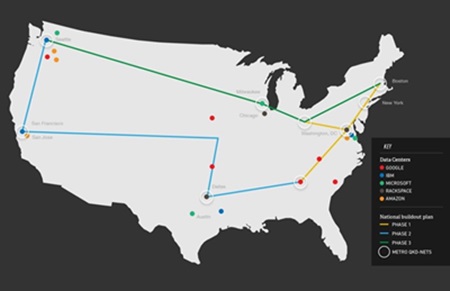
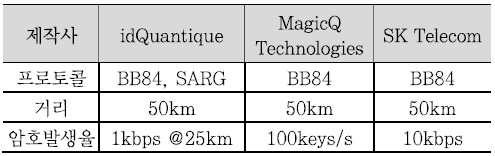
양자암호통신 장비는 미국의 MagicQ, 스위스의 ID Quantique, 일본의 도시바 등이 있으며, 한국은 SKT, KIST 등이 개발을 완료하였거나 개발 중에 있다. <표 2>에 각 사의 양자암호통신장비에 대한 규격을 정리하였다. 양자난수발생기의 속도가 낮아서 키 생성 속도가 크게 개선되지 못하고 있고, 실용적인 거리는 50km 정도로 장거리 전송에도 문제점이 있으며, 보안인증기술, 1:1 통신에 국한한 점 등 해결해야 할 문제점들이 있다. 장거리 전송을 위해서는 신뢰노드(Trusted Node Relay)에 의한 생성된 암호키를 전달하는 방법과 양자상태를 직접 전달하는 텔레포트를 이용한 양자리피터(Quan-tum Repeater) 방법, 위성을 이용한 전송방법이 있다. 중국은 2013년부터 2016년까지 베이징에서 상하이에 이르는 2,000km에 대해 50개 정도의 신뢰노드를 통하여 (그림 3)과 같이 장거리 양자암호통신 백본을 구축 중이며 주요 고객으로는 중국공산은행, 신화통신, 중국은행업감독관리위원회로써 은행전산망에 적용하고자 한다. 양자리피터에 의한 전송이 실현된다면 키 분배뿐만 아니라 양자상태를 직접 전달할 수 있으므로 양자시뮬레이터나 양자컴퓨터의 연결에도 응용 가능하지만 전송거리, 얽힘광자 생성속도, 양자메모리, local qubit과 flying qubit 간의 변환, 통신 가능한 파장대로 변환 등 구현의 문제에서 연구가 더 필요하다. 위성을 이용하는 방법은 위성에서 광자를 지상국으로 전송하는 방법으로 여러 개의 지상국에 대해 양자상태를 전송할 수 있는 장점이 있으나 실험적으로는 증명되지는 않았다. 이러한 QKD 백본으로 미국 Battelle사는 2015년을 목표로 Battelle 본사인 오하이오주 콜럼버스시에서 와싱턴DC 지역까지 770km를 신뢰노드를 사용하여 연결하고 있으며, (그림 4)와 같이 향후 구글, 아마존 등의 데이터센터를 연결하는 장거리 양자백본망을 구축할 예정이다. 유럽은 2008년 오스트리아 빈 지역의 4개의 노드를 연결하는 SECOQC 프로젝트를 통하여 신뢰노드 적용 가능성 및 문제점 등을 점검하였다. 최근에는 WDM-PON(Passive Optical Network) 적용 기술[7], 25km 텔레포트 기술[8], 307km 장거리 QKD 기술[9] 등이 개발되고 있다.

<표 2>

양자암호통신 상용장비 규격

(그림 3)

중국의 양자백본

(그림 4)

미국의 양자백본 계획

<출처>: The Verge,“Building a Global-Spanning Quantum Internet,” 2014.

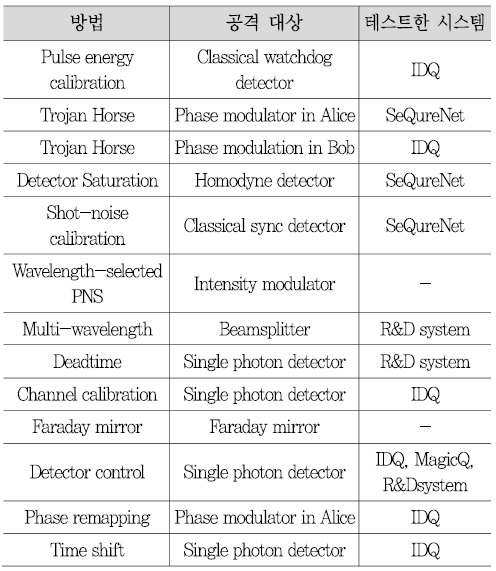
향후 연구주제로는 키 생성 속도 향상, 다중 신뢰노드 간 연동, 양자리피터 개발 및 적용 시험, MDI(Measurement Device Independent), CV(Continuous Variable) QKD 등 새로운 프로토콜 개발, 서로 다른 양자 노드 간의 광학 연결 등이 있을 것이다. 또한, 이론적으로는 무조건 안전성이 확보되었지만 구현된 실제 시스템에서 해킹이 불가능하지 않다는 것이 알려져 있다. 가장 간단한 방법으로는 photon number splitting 방법이다. 실제 QKD 시스템에서는 가격, 거리 등 여러 가지 이유로 단일광자를 사용하지 않고 레이저를 감쇄기에 통과시켜서 매우 약하게 만든 빛(weak laser pulse)을 사용하는데 광자들이 2개 이상 존재할 수 있으므로 통신 도중에 광자를 분리해서 읽어볼 수 있다는 것으로, 이에 대한 방어로 Decoy 상태 프로토콜[10], SARG04 프로토콜[11], Distributed phase reference 프로토콜[12] 등을 추가로 탑재하여 사용하게 된다. <표 3>에 실제 상용시스템에서 공격 가능한 다양한 방법을 정리하였다[13].

<표 3>

양자암호장비의 공격 예

또한 QKD 기술 이외에도 새로운 양자프로토콜을 적용하여 다음과 같은 응용도 가능하다.

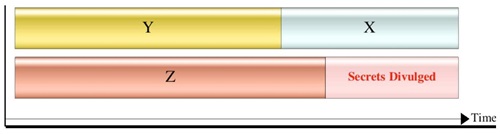
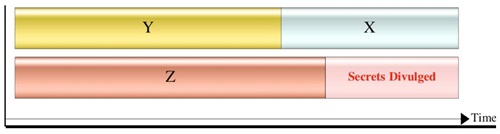
이 기술들은 기존의 현대 암호체계를 보완하는 것도 있으며, 고전적인 방법에서는 불가능했던 것을 가능하게 해주는 것도 있다. BB84로 시작된 양자암호 관련 기술은 단순한 암호의 분배를 넘어서 현대 암호와 보완적 관계로 적용범위를 넓혀나갈 수 있을 것이다. 이와는 별도로, 양자컴퓨터의 특정알고리즘(Shor's Algorithm)에 의해 지수적으로 빨리 소인수분해가 가능하게 되어 소인수분해에 근거한 RSA 암호체계가 위협을 받을 가능성이 있다. 이에 따라서 새로운 안전한 암호가 만들어질 필요성이 대두되었고, 양자암호에 의해 정보가 보호되면서도 동시에 양자컴퓨터로 암호가 깨질 수 있게 되었다. 따라서, 최근 유럽의 ETSI를 중심으로 Quantum-Safe라는 표현을 새롭게 만들었는데 이는 2가지의 중첩된 뜻을 가지게 된다. 즉, 양자암호기술에 의해 보호되고 양자컴퓨터로부터 보호되어야 한다는 것이다. (그림 5)는 양자컴퓨터의 개발시기(Z)가 양자암호통신체계 구축시기(Y)와 양자컴퓨터가 깰 수 없는 암호체계 개발기간(X)를 더한 시기보다 짧으면 보안이 깨질 것이라는 것을 나타내고 있다. 따라서 양자컴퓨터로부터 안전하지만 계산능력이 많이 필요하지 않는 새로운 암호체계를 연구해야 할 필요성이 대두되었고 이를 Post Quantum Cryptography라고 한다.

(그림 5)

Quantum-Safe Cryptography의 필요성

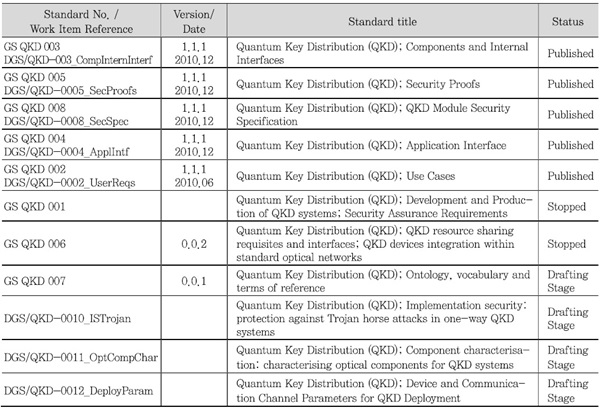
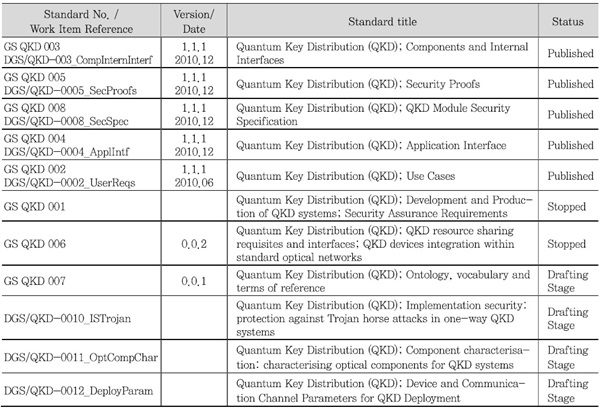
양자암호에 대해서는 ETSI를 중심으로 표준화가 이루어지고 있으며 <표 4>에 ETSI의 표준문서에 대한 동향을 정리하였다. 양자암호를 적용하게 될 경우 다음과 같은 기존 정보통신관련 국제표준에 대해 변경 또는 수정이 필요할 것이다.

<표 4>

ETSI의 양자암호 관련 표준화 현황

시장 관점에서 양자암호 및 양자통신 기술의 문제점에 대해 살펴보면 다음 4가지 측면에서 고려해야 할 사항을 기술개발 및 제도보완 등의 방법으로 개선되어야 할 것이다.

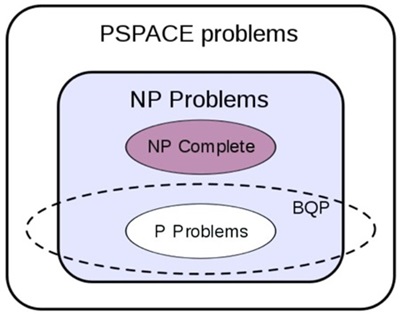
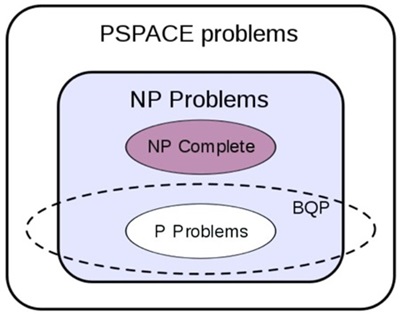
1982년 Feynman[1]은 양자역학의 상태공간은 힐버트 공간으로 n개의 시스템이 있을 때 이를 표현하는 상태공간은은 2ⁿ이어야하고 각각의 상태는 모두 복소수 형태이어야 하므로 양자역학적 시스템에 대한 고전 컴퓨터로의 모사가 불가능하다고 말했다. 그것은 역으로 양자역학적 시스템을 제어할 수 있는 컴퓨터가 만들어진다면 고전 컴퓨터보다 뛰어날 것이라는 가설이다. 1985년 Deutsch[2]에 의해 양자컴퓨터는 범용튜링머신임을 밝히고 양자병렬성(quantum parallelism)에 의해 특정 확률론적 문제에 대해서는 고전컴퓨터보다 빠르다는 점을 논의하였다. 양자컴퓨팅은 양자상태로 표현된 데이터에 대해 양자역학적 현상(중첩, 얽힘, 상호작용 등)을 사용하여 연산하는 과정을 말한다. 정보이론과 결합한 양자컴퓨터에 대한 알고리즘은 처음 제안 후 10년이 지나서야 가능하게 되었는데, 1996년 Shor[15]는 소인수분해를 지수적으로 빨리 수행할 수 있는 양자알고리즘을 발표하였고, 같은 해 Grover[16]는 다항식적 검색속도 향상의 양자검색알고리즘을 발표하였다. 이 발표 이후 여러 가지 양자알고리즘이 발표되었고 그 중에서 HSP(Hidden Subgroup)의 양자알고리즘을 개발하게 되어 graph 문제 등을 풀 수 있게 되었다. 또한, quantum random walk으로 다항식적 속도향상(polynomial speedup)을 얻을 수 있었다. NIST는 Quantum Algorithm Zoo[14]라는 웹 사이트를 운영하여 양자알고리즘 리스트를 관리하고 있는데, 대수이론, 질의응답, 근사 및 모사의 3가지 구분에 대해 총 52개의 알고리즘을 분류하고 있다. <표 5>에 분류된 알고리즘들을 리스트하였다. 대부분의 경우 고전컴퓨터에 비하여 다항식적 속도향상을 가져오는 것으로 보고하고 있다. 1997년 Bennett 등[17]은 NP 문제에 대해 양자튜링머신이 O(^2n/m)(m=2 or 3) 이상 빨라질 수 없다는 점을 밝힘으로써 고전 컴퓨터가 풀 수 없는 모든 문제를 해결할 수 있지는 않다는 점을 알게 되었고, 특별히 양자컴퓨터가 다항식적 시간 내에 풀 수 있는 문제의 범위를 BQP(Bounded error, Quantum, Polynomial time)라고 하고 그 범위가 확정된 것은 아니고 아직도 연구 중에 있으며 현재까지 알려진 대략적인 범위는 (그림 6)과 같다.

<표 5>

Quantum Algorithm Zoo의 양자 알고리즘 리스트[14]

(그림 6)

BQP 문제의 범위[18]

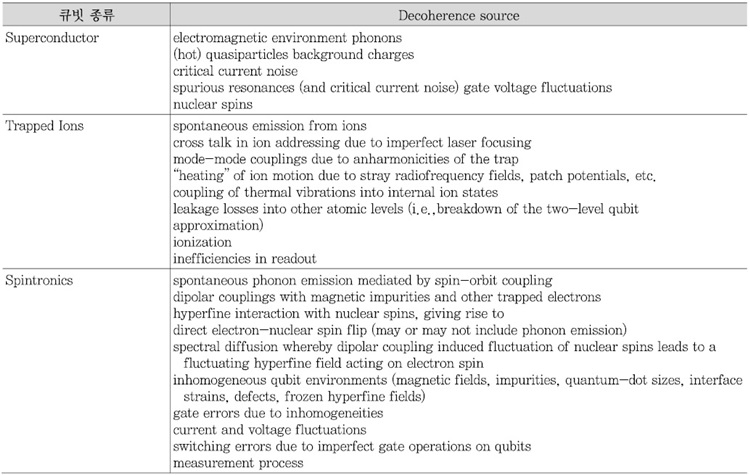
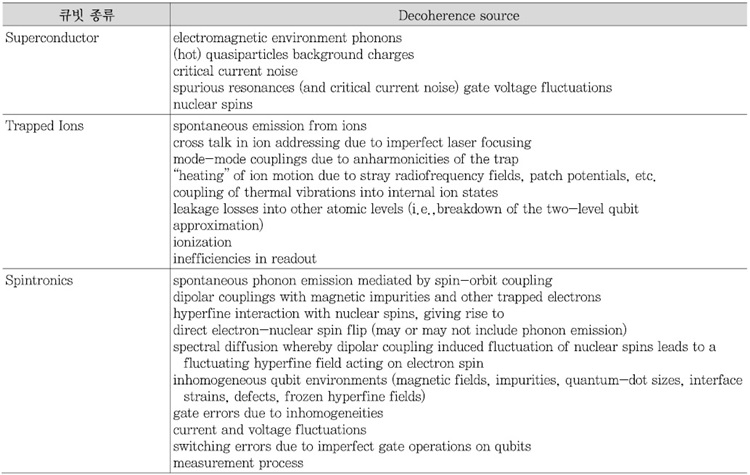
양자컴퓨터의 속도향상은 양자알고리즘에 의해서 다항식적 또는 지수함수적으로도 가능하다는 점이 수학 및 전산학적인 측면에서 연구되고 있는 반면, 실제 양자상태를 만들어내고 연산하는 양자프로세서는 여러 가지 방법에 의해 물리학적, 전자공학적으로 연구되고 있다. 현재까지 유망한 소자 및 이를 사용한 양자컴퓨터의 가능성에 대해 (그림 7)에 나타내었다. D-Wave사는 500~2,000개의 초전도 플럭스 큐빗을 사용하여 Simulated Anealing의 양자버전인 Quantum Anealing 모사방법을 수행할 수 있는 최초의 양자컴퓨터를 만들었다. 그러나, 앞서 언급한 알고리즘들을 모두 수행할 수 없고, 단지 근사 및 최적화 알고리즘을 수행할 수 있다. 그럼에도 불구하고 구글, NASA 등에서 패턴 매칭, 최적 경로탐색 등 문제를 풀기 위해 도입하였다. 그 외 방법들은 모든 알고리즘들을 수행할 수 있는 양자컴퓨터로 개발 가능한데, 10년 후 사용 가능한 수준에 도달할 만한 것으로 초전도 큐빗[20], 이온포획(ion trap) 큐빗[21]이 있다. 현재까지 알려져 있는 현황은 초전도의 경우는 5개 정도의 큐빗이 가능하고 수십 mK 정도로 극저온기술이 필요하며, 이온포획은 15개 정도의 큐빗이 가능하며 진공챔버와 피코초펄스레이저 등이 필요하다. 그 외에는 원자 및 전자의 스핀을 사용한 큐빗[22]도 연구 중이나 2개 정도의 큐빗이 가능한 정도인 반면 반도체 공정으로 가능하다는 점은 집적화 및 산업화 가능성이 있음을 시사한다. 3가지 방법에 의한 큐빗들은 단일이온, 단일초전도회로, 단일스핀 등을 이용하는 관계로 외부 영향 등에 의해 결맞음(coherency)을 잃어버리게(decoherence)되어 양자상태를 기록하였다 하더라도 보전되지 않고 필요한 연산시간 동안 유지하지 못하는 오류가 발생한다. <표 6>은 decoherence 원인에 대해 밝힌 것이다. 따라서, 양자상태에 변화를 보정하는 과정이 필요한데 이러한 과정을 오류보정(quantum error correction)이라고 하며 양자상태의 성질 및 큐빗의 공간적 형태 등에 따라 적절한 방법을 사용하여 오류보정을 함으로써 불안한 물리큐빗에서 외부영향이나 시간에 따라 변하지 않는 논리큐빗이 만들어지게 된다. 그러나, 1개의 논리큐빗을 만들기 위해 많게는 49개, 적게는 3개 물리큐빗이 필요[23]하므로 많은 비용이 소요될 수 있다. 이러한 방법에 의한 양자컴퓨터 모델은 회로 기반 양자컴퓨터(circuit based quantum computer)로 많은 큐빗을 필요로 하는 반면 직관적이고 이해하기 쉬우며 고전 컴퓨터의 프로그래밍 언어로도 표현가능하고 컴파일 과정을 통해 양자 연산코드로 만들어내는 자동화가 가능[24]하므로 실용적 양자컴퓨터로의 접근이 어렵지 않다. 또 다른 양자컴퓨터 모델로는 토폴로지 모델(Topology based quantum computer)[25]이 있는데, 아직 이론적으로도 연구되어야 할 부분이 많이 있고 사용 가능한 큐빗도 구현되어 있지 않으나 오류보정이 필요없다는 점이 장점으로 구현에 성공한다면 가장 강력한 후보가 될 가능성이 있다.

(그림 7)

유망 양자소자에 의한 양자컴퓨터 비교[19]

<표 6>

Decoherence을 일으키는 물리적 원인

이러한 기술들을 바탕으로 안정적으로 동작하는 양자컴퓨터가 만들어짐을 전제로, 응용 측면에서 볼 때 4가지 양자알고리즘이 사용된다. Quantum amplitude am-plification, quantum Fourier transformation, quantum random walk, quantum simulation이 있으며, 데이터들이 양자데이터로 쉽게 변환 가능할 때 양자컴퓨터의 실제 응용이 가능할 것이고 최종 응용은 quantum machine learning이 될 것이다[26]. 대부분 이론적 연구이지만 고전학습이론 알고리즘에 대해 양자데이터와 위의 4가지 양자알고리즘군들을 사용함에 따라 제곱 또는 지수적으로 속도향상이 될 것으로 보고되고 있다[27]. Grover의 탐색알고리즘을 사용한 경우는 제곱으로 속도향상을 보고되고 있으며 지수함수적 속도향상은 입출력 데이터가 양자데이터라는 시나리오에 가능한 것으로 보고된다. 또한, 양자빅데이터 분석의 경우 고전 컴퓨터는 데이터 사이즈에 대해 다항식 시간이 걸리는 데 비해 vector와 tensor를 다루는 데에 적합한 양자컴퓨터는 데이터 사이즈에 대해 로그함수적으로 속도를 나타냄을 보고하고 있다[28].

양자과학의 이론과 물리학 실험실 수준의 양자역학은 정보이론과 결합하여 새로운 응용분야인 양자정보통신을 만들어내고 있으며 기존 정보통신의 범위와 해결할 수 있는 문제의 범위를 넓힐 수 있다. 2002년 Fuchs[29]는 영자역학은 quantum computing, quantum information theory, quantum cryptography의 3개의 응용분야로 나누어질 수 있음에 대해 보여주었고, 본고에서는 정보통신 응용의 측면에서 양자통신과 양자컴퓨팅의 동향을 살펴보았다. 양자통신은 광섬유를 사용한 양자암호통신이 상용화 단계에 이르렀고 보안성을 더욱 향상시키고 네트워크로의 확장성을 확보하기 위한 연구가 진행되고 있다. 양자컴퓨팅은 하드웨어가 10년 정도면 가능할 것으로 예상됨에 따라 수학 알고리즘적 접근에서 전산학적 응용을 위한 접근이 이루어지고 있으며 최근 화두인 빅데이터 분석, 머신러닝, 인공지능의 분야에 응용가능성을 연구하고 있다. 소자 측면에서는 확장 가능한(scalable) 수준으로 개발되고 있으므로 10년 내에는 양자알고리즘을 적용한 양자컴퓨팅도 가능하게 될 것이다.