양자컴퓨팅시스템 개발 및 활용 동향
Trends of Quantum Computing System Development and Applications
- 저자
- 최병수 / 양자창의연구실
- 권호
- 31권 2호 (통권 158)
- 논문구분
- 일반 논문
- 페이지
- 84-94
- 발행일자
- 2016.04.01
- DOI
- 10.22648/ETRI.2016.J.310209
- 초록
- 지난 60여 년간은 고전정보에 기반한 통신, 저장, 처리 능력이 비약적으로 발전하였다. 이 과정에서 가장 많이 사용된 방법은 정보소자의 크기를 감소시키는 방법이었는데, 이러한 접근법은 최근에 그 한계에 도달하고 있다. 이러한 한계를 극복하기 위해서 다양한 접근법이 연구되고 있으며, 궁극적으로는 양자역학적 현상에 기반하는 양자정보가 사용될 것으로 예상된다. 양자정보는 크게 계산성과 보안성을 향상시키는데, 이에 따라서 향후 ICT 전반에서 많은 변화가 생길 것으로 예상된다. 본고에서는 특히 양자정보에 기반한 양자컴퓨팅을 중심으로, 양자정보의 발현과 관련한 역사적 흐름, 양자정보에 기반한 정보처리의 핵심요소, 양자컴퓨팅 구현 방법론, 양자컴퓨팅 활용 방법론, 현재의 기술수준을 소개한다. 마지막으로 ICT의 경제의존도 및 사회몰입도가 높은 우리나라가 이러한 ICT패러다임의 전환기에서 과연 무엇을 어떻게 준비해야 하는지도 살펴본다.
Share
Ⅰ. 서론
자연현상을 해석하는 현재까지의 가장 정교한 이론체계는 양자역학이다. 특별히 입자크기 수준의 미시계에서는 양자역학적 현상이 지배적이지만, 일상수준과 같은 거시계에서는 잘 나타나지 않는다. 그러한 이유로 양자역학적 현상의 근본원리에 대해서는 아직도 명확히 이해하지 못하고 있다[1].
한편, 정보기술은 지난 60여 년간 지속해서 발전하였다. 이 과정에서 정보라 함은 암묵적으로 0 또는 1로 표현 가능한 이분법적 특성을 갖는 개념으로 여겨졌으며, 물리적으로도 그러한 개념을 표현할 수 있는 방법들이 주로 적용되었다. 이러한 발전 과정에서 가장 분명한 방향성 중 하나는 정보를 표현하는 정보소자의 크기가 지속적으로 작아졌다는 것이다. 이렇게 지속적으로 작아진 정보소자 덕분에 우리는 초창기 슈퍼컴퓨터보다도 복잡한 연산을 현재의 스마트폰에서도 손쉽게 해결할 수 있다.
하지만 지난 60여 년간의 정보소자에 대한 극소화도 점진적으로 그 한계에 도달하고 있다. 정보소자를 지금과 같은 고전적 정보표현방식(bit, 0 또는 1이 배타적으로 존재하는 방식)으로 구현하는 방식을 사용하는 경우, 정보소자의 극소화 과정에서 0과 1의 경계가 모호한 양자역학적 상태가 나타나기 시작하였다. 따라서, 이러한 양자역학적 상태를 억제하면서 고전정보표현방식을 적용하기 위해서는 기존 소자방식보다 더 큰 비용이 발생한다. 이러한 이유로 지금과 같은 고전적 정보표현방식을 사용하는 정보소자의 극소화는 더 이상 성능향상에 도움이 되지 않게 되었다[2].
이러한 문제점을 해결하기 위해서 다양한 접근법이 고려되었지만, 가장 혁신적인 방법은 양자정보소자에서 나타나는 양자역학적 현상을 억제하는 것이 아니라 이러한 특성을 역으로 이용하는 방법이다. 즉, 기존의 고전적 정보표현방식을 넘어서서 양자역학적 특성을 정보로 정의하는 것이다. 이처럼 양자역학적 현상을 갖는 물리적 상태를 정보로 활용한다는 측면에서 양자비트, 혹은 큐비트(quantum bit, qubit)라고 지칭한다.
이러한 정보표현의 원천적 변화(비트에서 큐비트로의 변화)는 ICT전반에서의 패러다임 수준의 변화를 의미한다. 정보의 정의가 달라지는 만큼, 정보의 수집, 저장, 전송, 처리과정에서 모두 변화가 요구되며, ICT가 수행할 수 있는 일의 범위 및 효율성도 더욱더 확대된다. ICT측면에서는 양자정보를 통해서 기존에는 어려웠건 혹은 해결 불가능했던 다양한 문제들을 쉽게 혹은 효율적으로 해결할 수 있게 되었다. 일례로, 양자통신을 이용하면 절대보안수준의 보안키분배가 가능하다[3]. 전반적으로는 정보를 수집하는 센서의 정교함이 높아지고, 정보를 전송하는 통신의 보안성이 높아지며, 정보를 처리하는 컴퓨팅의 계산성이 높아진다.
본고에서는 이러한 ICT의 근본적 변화를 야기하는 양자정보에 대한 역사적 측면, 양자정보를 활용하는 양자컴퓨팅모델의 발전역사, 그리고 현재 진행되고 있는 양자컴퓨팅 관련한 연구개발동향을 살펴본다. 또한, 이러한 일련의 분석을 통해서 향후 우리나라가 21세기 새로운 ICT패러다임 전환기에서 선제 연구개발과 이를 통한 ICT경쟁력 강화를 위해서 어떠한 연구개발 방향성과 로드맵을 가져야 하는지도 살펴본다.
Ⅱ. 정보표현의 극소화 및 양자정보의 출현
1. 고전정보소자의 극소화 진행
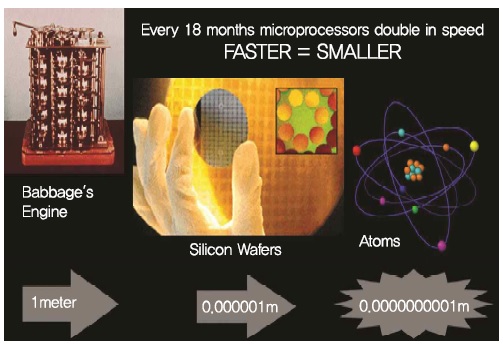
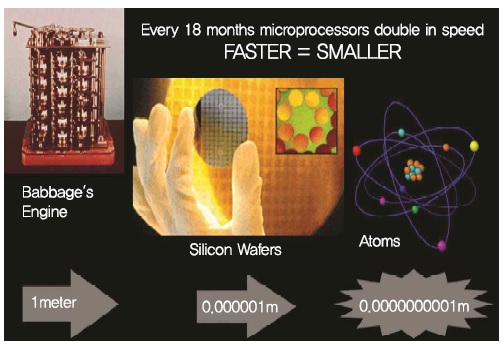
주판과 기계식 정보표현의 방식을 넘어서, 전자식 정보표현의 방식은 진공관부터 시작되었다고 할 수 있다. 이러한 정보표현방식은 정보표현장치의 크기가 지속해서 작아지면서 트랜지스터까지 발전하게 되었다. 이러한 트랜지스터도 처음에는 크기가 매우 컸지만, 제조기술의 지속적 발전으로 크기가 지속적으로 작아지게 되었다. 이에 따라서, 단위면적당 집적(저장)할 수 있는 정보처리량(정보량)은 18개월(매1년)마다 약 두 배 증가하게 되었다[(그림 1) 참조][4].
2. 고전정보소자 극소화의 근본적 한계
고전정보소자의 지속적인 크기 감소는 본질적으로 정보소자의 절대적 크기를 감소시키는 방법에 기반을 두는데 이러한 크기 감소는 무한정 진행될 수는 없다. 정보소자의 크기가 작아지면, 양자역학적 현상이 지배적으로 나타나게 되는데, 이러한 상황에서는 고전정보를 정확하게 표현하기가 어려워진다. 이러한 이유로 최근의 반도체 공정기술은 10나노미터 크기부터 발전속도가 급격히 느려지게 되었다[2].
3. 고전정보에서 양자정보로의 전환
이러한 근본적인 한계를 돌파하기 위한 대안으로써 이제는 정보표현방식을 바꾸어서 고전정보가 아닌 양자정보로의 변환이 고려되었다. 이는 극소화된 정보소자에서 지배적으로 나타나는 양자적 현상을 역으로 이용하여 양자적 특성을 갖는 정보를 사용하는 것을 의미한다. 고전정보를 bit(binary digit의 약자)라 할 때, 이에 대응하는 양자정보는 quantum bit, 약어로 qubit(큐비트)로 지칭된다[5]. 이러한 접근법은 정보소자의 극소화에 따른 이득은 포기하고, 대신에 양자정보가 갖는 정보학적 강점을 활용할 수 있다는 측면에서 소자크기를 더 이상 극소화하는 과정에서의 문제점은 회피하면서, 성능향상의 효과를 달성할 수 있다는 것을 의미한다.
4. ICT측면에서의 양자정보 해석
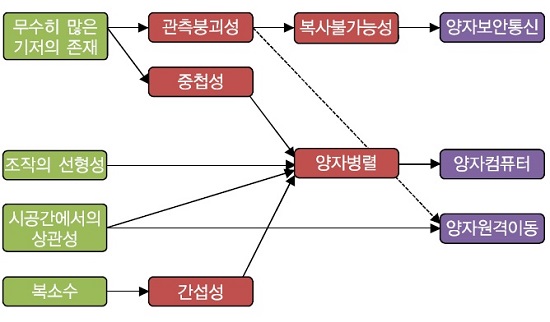
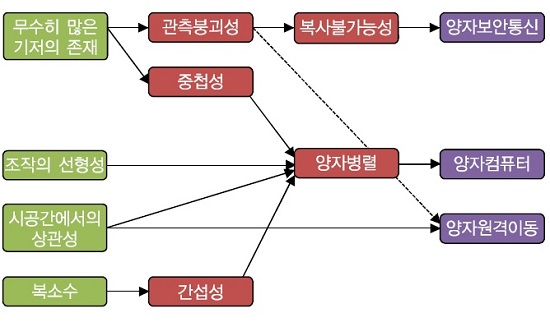
양자역학적 특성을 갖는 양자정보를 ICT측면에서 이해하는 것은 매우 중요하다. 주요한 양자역학적 특성을 ICT의 관점에서 정리하면 다음과 같다[(그림 2) 참조][6].
가. 양자중첩상태는 메모리 압축효과로 해석
양자정보에서 나타나는 중첩현상은 하나의 양자정보 단위(큐비트)는 두 개의 직교하는 기저에서 표현 가능한 모든 선형조합을 표현할 수 있음을 의미한다. 따라서, 고전정보에서는 비트당 표현할 수 있는 값이 0 혹은 1인데 반해서, 양자정보는 0과 1의 모든 중첩상태를 표현할 수 있다. 각각 n개의 단위를 사용한다고 가정할 때, 고전정보는 2^n개 조합 중 한 개의 값만을 표현할 수 있지만, 양자정보는 2^n개의 모든 조합을 중첩상태로 표현할 수 있다. 이러한 특성을 정보저장능력의 측면에서 해석하면, 표현하고자 하는 정보량에 대해서 고전정보는 동일한 비트수가 필요한데 반해서, 양자정보는 로그수준의 큐비트수가 필요하다. 결과적으로 정보표현과정에서 마치 압축효과가 나타난다고 볼 수 있다. 이러한 압축효과는 통신과 계산과정에서 대역폭이나 연산복잡도를 낮추는데 핵심적으로 작용한다.
나. 양자간섭현상은 효율적인 병렬계산으로 해석
간섭현상은 기저가 동일할 경우, 기저별로 존재하는 복소수 위상값들이 합산되는 과정에서 발생한다. 위상이 복소수인 관계로 간섭현상은 보강간섭 혹은 상쇄간섭현상이 나타난다. 이는 마치, 두 개의 파도가 만나는 과정에서, 동일한 위상을 가질 때는 파도가 더 커지지만, 정반대의 위상을 가질 때는 파도가 사라지는 현상을 의미한다. 이러한 간섭현상은 정보처리 과정에서 병렬연산과정으로 해석될 수 있는데, 연산과정이 모든 기저에서 동시에 일어난다는 것이 특징이다. 양자간섭현상은 주로 병렬계산과정에서 사용된다.
다. 양자얽힘상태는 원거리 상관성으로 해석
얽힘현상은 시공간적으로 떨어져 있는 두 개 이상의 양자정보가 서로 간에 강한 상관성을 갖는 것을 의미한다. 얽힘현상은 물리학적으로는 두 개 이상의 양자정보가 하나의 전역적 특성을 갖도록 조직화되었음을 의미한다. 이러한 현상은 우리 인간이 실생활에서는 거의 확인할 수 없고 양자수준에서만 확인할 수 있으므로, 다양한 양자역학적 특성 중에서 가장 받아들이기 힘든 특성이다[7]. 이러한 얽힘현상을 ICT의 관점에서 해석한다면, 시공간적으로 떨어져 있는 두 개의 양자정보가 있을 때, 한쪽 양자정보에 적용되는 조작이 다른 양자정보에도 즉각적으로 영향을 끼친다는 것으로 해석될 수 있다. 단, 주의할 것은 이러한 영향이 즉각적으로 발생한다고 하더라도, 그것을 확인하고 활용하는 과정에서는 시공간을 이동하는 데 필요한 빛의 이동시간만큼은 요구된다는 점이다. 따라서, 얽힘은 비국지적현상이며, 한쪽에서의 조작은 즉각적으로 다른 쪽에 반영된다고 하더라도, 그것을 확인 및 활용하는 과정에서는 시공간이동 시간이 항상 존재한다. 양자얽힘상태는 주로 통신과정에서 양자정보의 전송이나 계산과정에서 입력과 함수값 사이에서의 상관성을 유지하는 과정에서 활용된다.
라. 관측붕괴현상은 일회성 읽기 과정으로 해석
관측붕괴현상은 관측의 주체인 고전세계가 관측의 대상인 양자세계를 접속하면서, 양자세계에 존재하는 특성이 급속하게 고전적 상태로 변환되는 것을 의미한다. 또한, 이러한 변환과정은 일회성이어서 읽기의 대상은 다시 원래의 양자상태로 돌아가지 못한다. 관측붕괴현상은 ICT측면에서 매우 깨지기 쉬우며 단 한 번만 읽을 수 있는 매우 민감한 정보를 다루는 것으로 해석될 수 있다. 이러한 특성이 더 확장되어서, 양자정보는 결과적으로 정보자체의 유일성을 항상 보장하게 된다. 결과적으로 관측붕괴현상은 주로 정보보안이나 정보의 유일성 보장등과 같은 영역에서 활용된다. 또한, 연산과정에서 특정한 값을 확인하거나 양자정보소자의 오류값을 확인하는 과정에서 주로 사용된다.
Ⅲ. 양자컴퓨팅모델의 출현
1. 양자시뮬레이션의 출현
양자역학적 현상에 대한 학문적인 접근은 플랑크로 대표되는 1900년대 초부터 시작되었다. 이후, 아인슈타인, 보어, 슈뢰딩거, 하이젠베르크, 파울리, 드브로이 등으로 대표되는 1920년대의 많은 이론/실험물리학자들에 의해서 양자역학은 완성도를 높여나갔다. 현재 일반상대성 이론과 함께 자연현상을 해석하는 가장 중요한 이론으로 자리 잡고 있다.
이러한 양자역학적 발전이 ICT측면에서 중요도를 갖기 시작한 것은, 파인만에 의해서 양자역학적 다체계 시스템을 고전컴퓨터로 시뮬레이션하는 과정의 어려움에 관한 연구가 시발점이라 할 수 있다[8]. 파인만은 다체계 양자역학적 시스템을 표현하고, 그것의 동역학을 처리하는 데에 필요한 고전적 계산량은 양자역학적 개체 수에 대해서 지수적으로 증가한다는 것을 확인하였다. 이를 계기로, 고전컴퓨팅을 이용하여 양자역학적 시스템을 전산모사할 수 없음을 확인하였지만, 역으로 양자역학적 특성을 갖는 컴퓨팅 시스템이라면 양자역학적 시스템을 전산모사 할 수 있다는 것 또한 언급하였다. 이 시점에서 처음으로 양자역학을 활용하는 시뮬레이션 시스템이 언급되었으며, 이것이 양자컴퓨팅의 가장 시초라 할 수 있다.
이 시대에 고려되었던 양자시뮬레이션은 현재의 의미에서는 양자 에뮬레이션, 즉, 또다른 양자다체계 시스템을 이용하여, 대상 양자다체계 시스템이 갖는 동역학을 그대로 적용하는 것을 의미하였다. 하지만, 이후 이러한 접근법은 더 발전하여, 하나의 양자다체계 시스템을 이용하여 임의의 양자다체계 시스템을 전산모사할 수 있는 만능의 양자시뮬레이션 개념으로 발전하였다[9]. 만능 양자시뮬레이션인 만큼 다양한 양자물리학적 현상을 시뮬레이션할 수 있으며, 이를 통해서 고전적으로는 확인하기 어려웠던 많은 이론들을 효과적으로 검증할 수 있을것으로 기대된다.
2. 양자컴퓨팅 모델
양자시뮬레이션은 물리학적 관점에서의 접근과 활용에 무게중심을 두고 있다. 반면, ICT측면에서 중요한 정의는 이러한 모델을 만능의 컴퓨팅 모델로 어떻게 정의하느냐이다. 이를 해결하기 위해서 가장 효과적인 방법은 튜링 머신을 정의하는 것인데, 이를 제안한 사람은 David Deutsch이다[10]. 기본적으로 양자튜링머신은 양자역학적 특성을 갖는 테이프와 헤드를 사용하는 방식으로 고안되었다. 양자역학적 테이프는 중첨상태를 의미하며, 양자역학적 헤드는 간섭계를 구현하는 시스템으로 해석된다. 이러한 모델을 통해서 만능의 계산이 양자정보기반에서도 구현 가능함을 확인하였다.
양자튜링머신은 개념적으로는 의미있지만, 실용적인 측면에서는 제한점이 많았다. 이러한 문제점을 해결하기 위해서 양자회로모델이 제안되었다[11]. 이러한 양자회로모델은 기본적으로 몇 가지의 양자만능게이트를 이용하여 모든 양자정보처리과정을 근사할 수 있다는 것에 근간하고 있다. 이는 고전적인 만능 컴퓨터가 NAND게이트만으로 구현되는 것과 같은 원리이다. 현재는 이러한 만능 게이트 집합 중에서 매우 간단한 3개의 단위 게이트인 H, T, CNOT을 주로 사용하고 있으며, 대부분의 양자ICT연구개발에서 사용되는 양자회로는 이러한 게이트들로 구성되고 있다.
3. 다양한 양자컴퓨팅 모델들의 출현
양자회로모델은 직관적이라는 측면에서는 강점을 갖지만, 실제 구현의 측면에서는 다양한 문제점을 갖고 있다. 특히, 공간적으로 떨어져 있는 두 개의 큐비트 사이에서의 비국지적 두 개 큐비트 게이트(예, CNOT)의 구현 등에서는 매우 큰 어려움을 수반한다. 이러한 기술적 문제점을 해결함과 동시에, 양자정보소자 기술별 구현의 용이성을 충분히 활용하기 위해서 다양한 모델이 제안되었다. 그 중에서 가장 많이 고려되는 모델은 관측기반형모델이다[12]. 이 모델에서는 만능게이트를 구현하는 과정이 큐비트에 대한 연속적인 관측으로만 구성되어 있으며, 이러한 관측과정은 선행 관측결과의 결과에 따라서 후행 관측기저의 동적인 변화를 유도한다. 이러한 구현 방식은 오로지 인접한 두 개 큐비트 사이에서의 CNOT만 요구되므로, 앞선 양자회로모델에 비해서 구현용이성이 높다.
이 외에도 다수 모델들이 제안되었다. 2차원 물리계에서 나타나는 위상학적 정보를 큐비트로 정의하고, 그러한 큐비트들의 기학적인 조작(braiding)으로 연산을 수행하는 위상학적 모델도 제안되었다[13]. 이러한 모델에서는 큐비트의 정의가 물리학적 시스템의 전역적 특성에 기반하므로, 기존의 큐비트 구현방식에 비해서 훨씬 안정적이다. 또한, 물리적으로 가장 안정한 상태로 자연스럽게 변환하는 과정을 이용하는 양자절연형 모델도 제안되었다[14]. 이 모델에서는 사용자의 알고리즘을 물리계의 가장 낮은 에너지를 찾는 문제로 변환하여 적용한다.
Ⅳ. 고전컴퓨팅 vs 양자컴퓨팅
1. 통신능력 측면
분산형 컴퓨팅 방식을 고려할 때, 목적으로 하는 연산을 수행하는 데 필요한 통신량은 적을수록 좋다. 고전정보의 경우에는 공간적으로 떨어져 있는 두 개의 노드 사이에서 상호간 정보를 전달하기 위해서는 정보자체를 전송하는 방법이 유일하다. 반면에, 양자정보에서는 선제적으로 얽힘 등을 공유할 때, 양자정보를 손쉽게 전송할 수 있으며, 이를 통해 분산형 계산에서 통신복잡도를 크게 낮출 수 있다[15]. 물론, 이러한 얽힘상태의 선제적 공유 과정에서 필요한 작업을 고려한다면, 전체적으로는 고전적 방식에 비해서 크게 차이는 나지 않는다.
2. 계산능력 측면
계산의 측면에서는 양자정보의 중첩, 간섭, 얽힘 등을 이용하여 처리하고자 하는 데이터 사이 혹은 입력데이터 값들에서 존재하는 전역적 특성을 쉽게 확인할 수 있다. 하지만, 특정한 하나의 값에 대한 연산결과를 유도해야 하는 것 등의 문제에서는 양자컴퓨팅의 성능향상효과는 거의 없다. 본질적으로, 양자컴퓨팅이 계산측면에서 높은 성능향상효과를 보기 위해서는 병렬계산이 많이 요구되는 문제들이다. 또한, 통상적으로 양자컴퓨팅을 사용하면 고전컴퓨팅을 사용하는 경우에 비해서 성능향상 효과가 나타나는 것을 기대하기 때문에, 양자알고리즘을 개발하는 것은 쉬운 일은 아니다[16].
3. 보안능력 측면
양자정보의 관측붕괴성, 복제불가능성[17], 표현방식에서의 임의성 등은 정보보호의 관점에서 다양하게 활용된다. 서로 약속된 정보 생성자와 전달자를 제외하고는 나머지 다른 개체에서는 양자정보를 정확하게 확인할 수 없도록 하여 상호간 비밀키를 분배하는 방법이 대표적이다. 또한, 양자정보의 복제불가능성에 기반하여 연산하는 과정에서의 모든 정보에 대한 노출을 억제할 수 있으며, 사용자의 정보에 대한 유일성을 보장하는 방법 등이 제안되었다.
Ⅴ. 양자컴퓨팅의 활용분야
1. 함수의 전역적 특성 파악 유형
주어진 문제에서 찾아내고자 하는 것이 주어진 함수의 전역적 특성을 파악하는 문제 유형이다. 양자컴퓨터는 이러한 문제에 대해서 모든 입력조합을 중첩의 상태로 처리하여, 모든 함수값을 중첩상태로 처리할 수 있으므로 고전적 접근법 보다 효율적이다. 또한, 이 과정에서 필요한 큐비트의 수도 적기 때문에 구현의 측면에서도 용이하다. 이러한 유형의 문제들로는 양자시뮬레이션, 양자대수분석[18] 등과 같은 것이 있다. 적은 큐비트수를 이용하므로 초기 양자컴퓨팅의 활용분야로 적합하다. 지금 현재 10~100개의 물리적 큐비트를 이용한 양자시뮬레이션 연구가 활발하다.
2. 데이터의 전역적 특성 파악 유형
이러한 유형의 문제는 함수의 계산은 단순하지만, 함수가 다루어야 할 입력 값이 인위적으로 주어지는 경우이다. 특히 함수를 통해서 파악하고자 하는 것은 주어진 임의의 데이터들에 대한 통계값을 추출하는 과정에 국한되는 경우이다. 양자컴퓨터는 이러한 상황에서 입력으로 인가되는 데이터를 적은 수의 큐비트 수로 표현하기 때문에 전체적으로 연산량이 감소하는 효과가 나타난다. 대표적인 분야로 빅데이터를 분석하는 과정인데, 빅데이터에 대한 양자메모리의 효율성이 적극적으로 활용된다[19]. 장기적으로 볼 때, 이러한 유형의 문제가 ICT분야에서 더 많으므로, 양자컴퓨팅의 가장 보편적인 활용분야가 될 것으로 여겨진다.
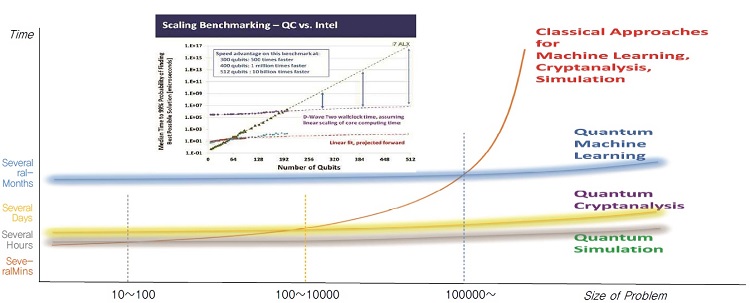
3. 고전컴퓨팅방식을 뛰어넘는 데 필요한 입력크기 기준
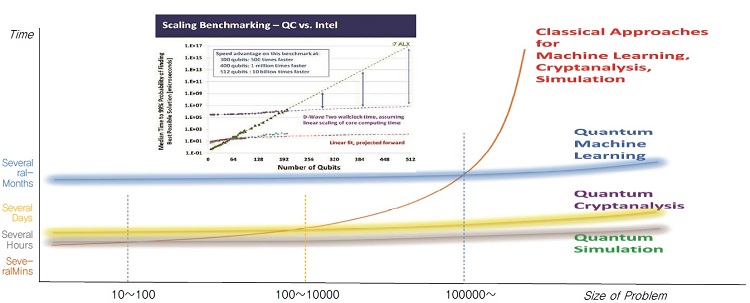
양자컴퓨팅의 구현과정에서의 복잡도 등으로 인해서, 양자컴퓨팅의 기대성능향상효과는 모든 입력크기에 나타나지는 않는다. 어느 일정수준의 입력크기 이상부터 양자컴퓨팅의 성능향상효과가 나타날것으로 예상되며, 이는 일정수준 이상의 큐비트 수를 갖는 양자컴퓨터가 필요하다는 것을 의미한다. (그림 3)은 양자컴퓨팅의 활용분야별 예상 최소 입력크기 혹은 최소 큐비트 수를 보여준다.
Ⅵ. 양자컴퓨팅 시스템 구조
1. 양자컴퓨팅 실현을 위한 기본적 조건들
양자컴퓨터도 기본적으로는 컴퓨터이므로, 통상적인 컴퓨터가 갖추어야 할 기본적인 기술적 기능을 충족해야 한다. 이와 관련하여 DiVincenzo가 이미 몇 가지 기술적 요구조건을 명시하였으며 대표적으로는 다음과 같은 조건들을 만족해야 한다[20].
첫째, 큐비트를 정의할 수 있고, 구현할 수 있어야 한다. 소자기술별로 큐비트를 정의하는 방식이 다르며, 그에 따라서 구현하는 방식이 다르므로 이러한 작업은 정보소자 의존적이다. 대표적인 방법으로 전자의 회전방향, 전류의 흐름방향, 광자의 파동방향, 입자의 에너지 상태 등을 큐비트로 정의한다.
두 번째, 큐비트들에 대해서 초기화가 가능해야 한다. 컴퓨팅을 실행하는 과정에서 초기상태를 확정해야 하므로, 큐비트들에 대해서 초기화하는 것은 가장 기본적인 조건이다.
세 번째, 큐비트들에 대해서 만능의 게이트를 구현할 수 있어야 한다. 구현의 어려움을 고려하여 가장 작은 집합으로써 H, T, CNOT게이트를 대상으로 한다.
네 번째, 큐비트들에 대해서 관측이 가능해야 한다. 계산 중간 과정이나 최종연산결과를 추출하는 과정에서 큐비트들을 관측해야 한다.
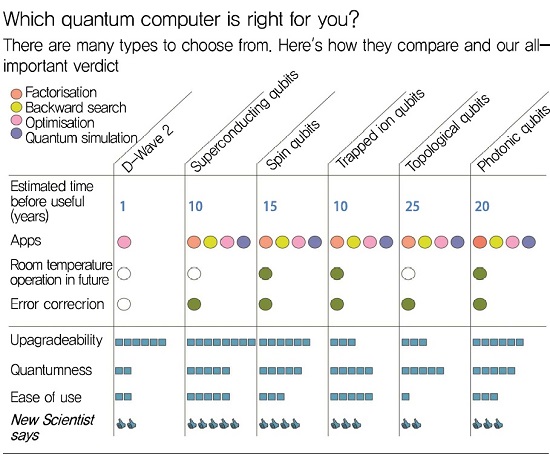
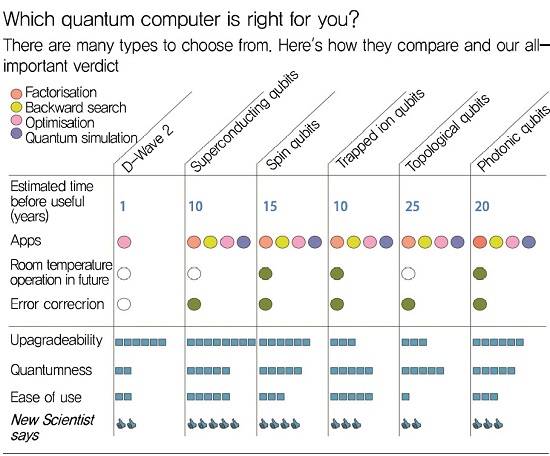
위와 같은 조건들은 양자정보소자기술의 기능적 측면에서의 요구조건이며, 각각의 기능들은 또한 성능적 측면에서 다양한 수준을 만족해야 한다. 일례로 연산결과의 신뢰도를 높이고, 통신거리 및 계산시간등을 충분히 확보하는 것을 고려하면 큐비트의 양자상태 유지시간이 길어야 하고, 초기화/게이트/관측 등의 모든 게이트의 동작 정확도가 높아야 한다. 이외에도 양자소자를 제어하는데 필요로 하는 고전적 처리 시스템의 성능도 매우 높아야 한다. (그림 4)는 현재 많은 연구가 진행되고 있는 큐빗소자 기술별 성능특성을 나타내고 있다.
2. 양자컴퓨팅의 안정성 확보를 위한 방법론
가. 오류보정방식
기본적으로 양자정보소자는 물리적시스템이므로 제어과정에서 오류값이 항상 존재한다. 반면, 수행하고자 하는 양자알고리즘등은 연산결과에서 높은 신뢰도를 요구한다. 그러므로, 물리적 큐비트를 알고리즘 수준에서 직접 사용하는 것은 상당한 무리가 있다. 이러한 문제점을 해결하기 위해서 고전적으로 많이 사용되는 오류보정방식을 양자정보에도 적용하는 방법이 제안되었다[22].
나. 결함허용방식
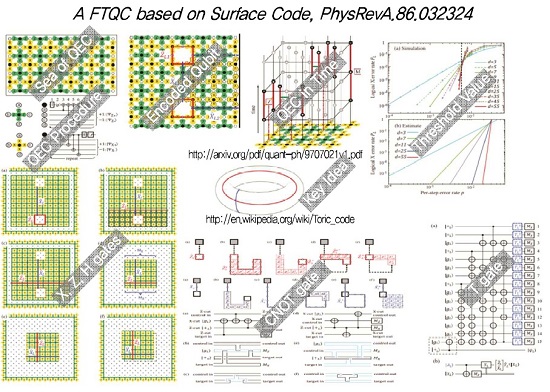
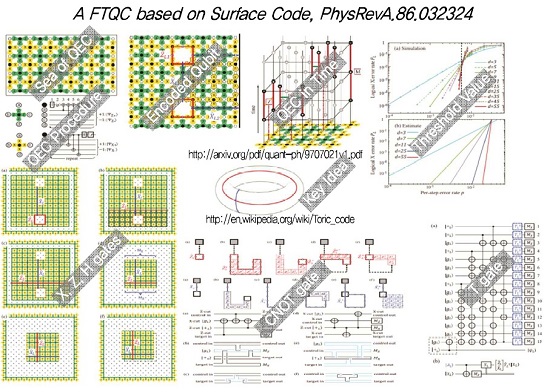
오류보정은 기본적으로 물리적 큐비트 등을 이용하여 안정성이 높은 논리적 큐비트 등을 만드는 과정에 대한 개념적 아이디어이다. 그러므로, 이것을 실제로 구현하는 과정에서는 구현하는 과정에서 추가되는 오류가 있음에도 원하는 오류보정이 가능하도록 설계해야 한다. 이렇게 오류를 갖는 조작을 적용함에도 원래의 목적대로 오류보정의 효과가 나타날 때 그러한 설계를 결함허용적이라 한다[23]. 또한, 논리적 큐비트만을 구현하는 것에서 확장하여 만능 연산이 가능하도록 하여 결함허용적 만능 양자컴퓨팅방식이 요구되는데, 이 과정에서는 앞선 만능게이트들을 모두 오류보정코드에 맞추어 결함허용적으로 재설계하는 과정이 요구된다[24]. 이러한 방법론에 따르면 양자정보소자가 일정수준의 오류값보다 낮으면 알고리즘수준에서 요구하는 높은 연산정확도를 충족시킬 수 있는데, 이때의 일정수준의 오류값을 임계오류값이라 하며, 양자컴퓨팅 구현에서 가장 중요한 성능요구값 중 하나이다. 이러한 임계오류값은 다양한 변수들을 고려하여 결정되기 때문에 하나의 특정한 값은 아니다. (그림 5)는 지금 현재 가장 많이 사용되는 오류보정코드인 surface code와 이를 이용한 결함허용 만능 연산모델[25]을 보여준다.
다. 일반적인 결함허용 만능 컴퓨팅 구현 방식
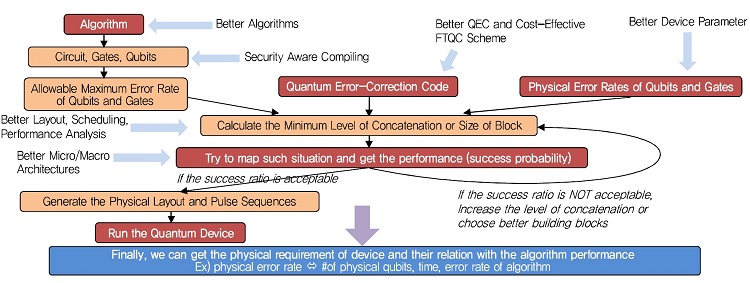
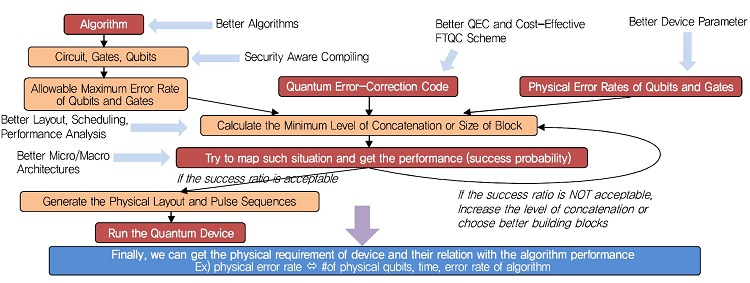
알고리즘수준에서 원하는 연산결과의 정확도와 소자수준에서 구현가능한 소자의 성능수준, 그리고 이 과정에서 사용되는 오류보정 및 결함허용방식간에는 (그림 6)과 같은 상관성을 갖는다. 알고리즘이 복잡할수록 알고리즘 수준에서의 큐비트와 게이트가 허용하는 논리적 오류값은 낮아지지만, 물리적 큐비트와 게이트의 오류값은 무한정 작아질 수 없기에 오류보정과 결함허용방식이 그 차이를 보정해주어야 한다.
이에 따라서, 알고리즘 수준에서의 허용 오류값을 만족할 수 있도록 하기 위해서는 오류보정과정을 반본적으로 적용해야 하는데, 이것이 (그림 6)에서의 오류보정코드의 적용 레벨 혹은 크기를 의미한다.
3. 양자컴퓨팅 시스템 구조
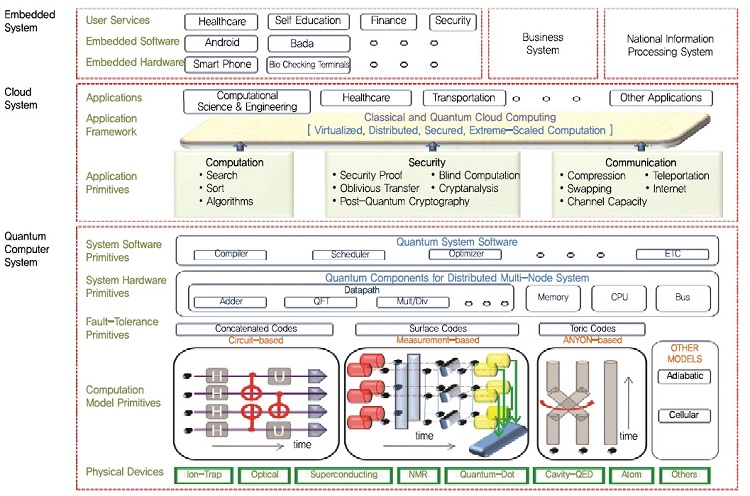
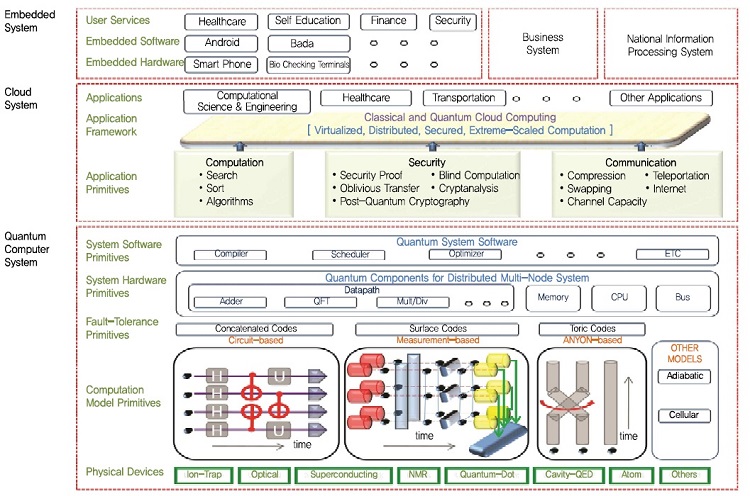
(그림 7)은 양자컴퓨팅을 포함한 양자ICT전반적인 구조를 의미한다. 가장 하단부 양자정보소자 구현기술부터, 중반부 양자통신과 양자컴퓨팅, 그리고 상단부 사용자측면에서의 활용분야를 의미한다. 이 중에서 양자컴퓨팅만을 고려하면 다음과 같다.
가장 하부구조는 양자정보소자를 구현하고, 이를 제어하는 물리적 계층이다. 주로 큐비트의 구현, 제어, 관측 등의 작업을 진행한다. 다음 단계에서는 이러한 물리적 계층구조를 논리적 계층구조로 바꾸기 위해서 오류보정-결함허용방식이 적용된다. 다음 단계에서는 논리적 빌딩블럭을 이용하여 논리적 양자컴퓨터를 조직화하는 단계이다. 통상적인 컴퓨팅 구조가 이 단계에서 대부분 반영된다. 다음 단계부터는 사용자를 위한 프로그래밍환경을 제공하는 것으로 주로 컴파일러등이 포함된다. 그리고, 마지막 단계에서는 다양한 기본 알고리즘 라이브러리를 제공하여 사용자로 하여금 범용적 목적으로 양자컴퓨팅을 사용할 수 있도록 도와준다.
4. 양자컴퓨팅 연구개발의 현재 수준
가. 하드웨어부분
양자정보를 표현하기 위한 하드웨어는 다양한 방식이 존재한다. 현재 많은 소자기술에서 큐비트의 수를 늘리는 연구에 집중함과 동시에 큐비트의 조작과정에서의 오류율을 낮추는 연구를 지속하고 있다[21].
나. 소프트웨어부분
통상적으로 양자정보 및 양자컴퓨터와 관련한 연구개발과제라 하면 대부분 양자정보소자의 구현과 같은 하드웨어를 고려하게 된다. 하지만, 이러한 하드웨어를 제어하여 사용자의 목적에 맞도록 조직화하고 운영한다는 측면에서 소프트웨어부분에서의 연구 또한 매우 중요하다. 실제로 양자컴퓨팅의 기대성능을 달성하는 데 가장 중요한 역할을 담당하는 것은 많은 경우 소프트웨어적 효율성에 의존하고 있다.
이러한 소프트웨어는 물리적 수준에서는 양자정보소자의 제어 및 평가, 오류보정-결함허용과정에서는 비용효율적이면서 고성능의 안정성확보를, 컴파일과정에서는 알고리즘의 성능향상을 주로 고려한다.
다. 종합적인 상황
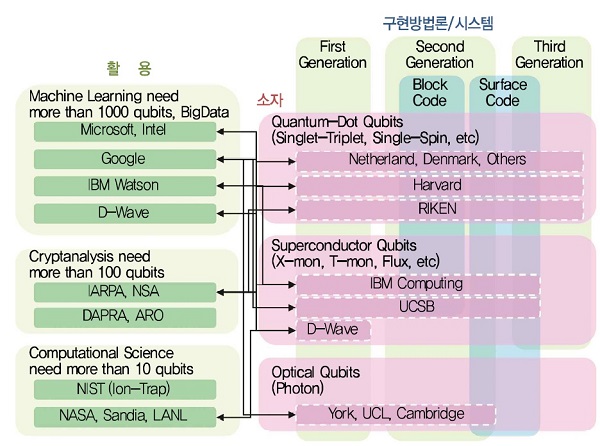
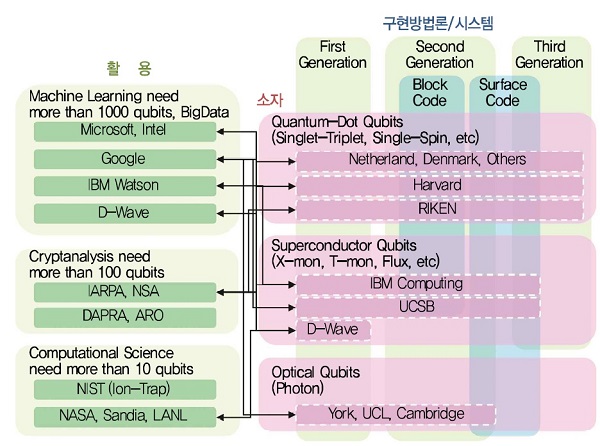
양자컴퓨팅과 관련한 하드웨어, 소프트웨어, 컴퓨팅모델, 활용분야 등을 고려하면 지금 현재 전 세계적으로 진행되고 있는 수준은 (그림 8)과 같다. 큐비트를 구현하는 측면에서는 고정형과 이동형방식이 주로 사용된다. 안정성 측면에서는 결함허용방식이 적용된 2세대형이 주로 사용된다. 활용분야에서는 큐비트수를 적게 사용하는 시뮬레이션분야가 주로 연구되고 있다. 하지만, 전체적으로는 아직 양자컴퓨팅을 구현하기 위한 원천연구개발 단계라 할 수 있다.
Ⅶ. 결론
본고에서는 양자정보의 출현배경, 양자정보기술의 발전추세, 그리고 양자ICT분야에서의 가장 핵심인 양자컴퓨팅 분야에서의 연구개발 동향에 대해서 살펴보았다.
양자컴퓨팅은 고전컴퓨팅이 제공하기 어려운 높은 수준의 보안성과 계산성을 동시에 제공하기 때문에, 향후 클라우드 환경에서 기존의 고전적 컴퓨팅 시스템을 대체할 것으로 예상된다. 이에 따라서, 양자컴퓨팅에 기반한 양자ICT는 기존의 고전ICT에 비해서 다양한 측면에서 매우 높은 효율성을 제공할 수 있을 것이며, 이로 인해서 인류는 지금까지 접하지 못했던 새롭고 효율적인 ICT서비스를 경험하게 될 것이다.
하지만, 이러한 ICT환경의 패러다임적 변화는 그냥 주어지는 것은 아니며 또한 학술적 연구만으로 이루어지는 것도 아니다. 그러므로, 우리나라와 같이 ICT에 대한 경제의존도 및 사회적 몰입도가 높은 나라에서 가장 적극적으로 연구개발을 진행해야 한다. 이러한 중요성을 간파한 다른 ICT거대기업들은 이미 수년 전부터 양자컴퓨팅분야에 집중투자를 하고 있는 것을 보아도 향후 어떠한 경쟁이 벌어질지 명확하다. 이에 따라서, 우리나라도 더 늦기 전에 본격적으로 관련 연구개발을 진행해야 하는데, 이제는 양자컴퓨팅, 양자통신, 그리고 양자ICT전반에 걸쳐서 장기적이고 실행 동력이 충분한 연구개발을 진행해야 한다. 이를 위해서 선행되어야 하는 것은 양자통신, 양자컴퓨팅, 양자ICT전반에 걸친 정교한 핵심이론 및 기술지도를 확보해야 하고, 이를 기반으로 연구개발참여 주체간에 효율적인 연구개발 로드맵을 작성해야 할 것으로 생각된다. 이러한 측면에서 한국전자통신연구원 양자창의연구센터는 우리나라의 향후 50년을 준비하는 양자컴퓨팅 관련 기술지도 및 연구개발 로드맵과 같은 청사진을 제시할 예정이다.
R. Feynman, “The Character of Physical Law, Chapter 6, 'I think I can safely say that nobody understands quantum mecahnics',” 1965.
M.A. Nielsen and I.L. Chuang, “Quantum Computation and Quantun Information,” Cambridge University Press, 2011.
R.P. Feynman, “Simulating Physics with Computers,” International J. Theoretical Physics, vol. 21, no. 6-7, 1982, pp. 467-488.
D. Deutsch, “Quantum Theory, the Church-Turing Principle and the Uni-versal Quantum Computer,” Proc. Royal Society of London A, vol. 400, no. 1818, 1985, pp. 97-117.
A. Barenco et al, “Elementary Gates for Quantum Computation,” Physical Review A, vol. 52, no. 5, p. 3457, Mar. 22nd, 1995.
R. Raussendorf, D.E. Browne, and H.J. Briegel, “Measurement-based Quantum Computation on Cluster States,” Physical Review A, vol. 68, no. 022312, Jan. 2003.
M.H. Freedman et al., “Topological Quantum Computation,” Bulletin of the American Mathmatical Society, vol. 40, no. 1, 2003, pp. 31-38.
E. Farhi et al, “A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem,” Science, vol. 20, no. 472, 2001.
G. Brassard, “Quantum Communication Complexity(A Survey),” 2001, http://arxiv.org/abs/quant-ph/0101005
P.W. Shor, “Why Haven't More Quantum Algorithms Been Found?”, Journal of the ACM, vol. 50, no. 1, 2003, pp. 87-90.
W.K. Wotters and W.H. Zurek, “A Single Quantum Cannot be Cloned,” Nature, vol. 299, 1982, pp. 802-803.
P.W. Shor, “Polynomial-Time Algorithms for Prime Factorization and Dis-crete Logarithms on a Quantum Computer,” SIAM Journal on Computing, vol. 26, no. 5, 1997, pp. 1484-1509.
D.P. DiVincenzo, “The Physical Implementation of Quantum Computation,” Fortschritte der Physik, vol. 48, no. 9-11, 2000, pp. 771-783.
D. Gottesman, “Theory of Fault-Tolerant Quantum Computation,” Physical Review A, vol. 57, no. 127, 1998.
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.