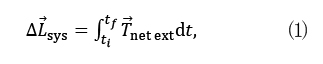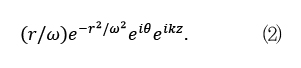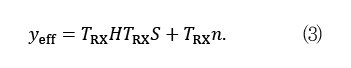홍주연 (Hong J.Y.) 전파자원연구그룹 선임연구원
이왕주 (Lee W.J.) 초연결원천연구본부 책임연구원
김중빈 (Kim J.B.) 무선전송연구실 선임연구원
김봉수 (Kim B.S.) 전파자원연구그룹 책임연구원
강민수 (Kang M.S.) 전파자원연구그룹 책임연구원
김광선 (Kim K.S.) 이동통신RF연구실 책임연구원
SongM.S. (송 명선) 전파위성연구본부 책임연구원
이호진 (Lee H.J.) 전파위성연구본부 책임연구원/본부장
조용희 (Cho Y.H.) 목원대학교 정보통신공학과 교수
Ⅰ. 전파 궤도 각운동량
1. 궤도 각운동량(OAM) 개념
뉴턴의 힘의 법칙에서 물체에 힘이 가해지면 운동을 하는데 이때의 운동량을 선운동량(Linear momentum)이라 하고, 물체가 원운동을 하기 위하여 토크(Torque)라는 돌림힘이 필요하며, 토크에 의한 물체의 운동량을 각운동량(Angular momentum)이라고 한다.
여기서, L은 각운동량, τ는 토크를 의미한다.
맥스웰(Maxwell) 이론으로부터 전자파 복사는 에너지와 운동량을 전달한다고 이미 알려져 있으며, 특별히 각운동량은 원형 편파의 특성을 보이는 스핀 각운동량 (SAM: Spin angular momentum)[1]과 공간적인 분포 특성을 보이는 궤도 각운동량(OAM: Orbital angular momentum)으로 구성된다[2].
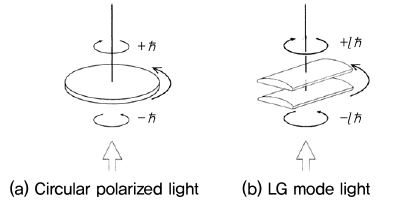
1936년, Beth[1]는 편파의 상태를 바꾸는 복굴절 판위에 편파광을 입사하면 토크가 만들어진다는 것을 추론하였고, (그림 1a)에서 보여지는 것처럼, 진공 상태의 좌현 편파(우현 편파)의 각운동량 ℏ(−ℏ)는 복굴절 판에 2ℏ의 SAM을 전달한다는 것을 실험적으로 증명하였다.
그리고 1992년 Allen은 Laguerre-Gaussian 모드 레이저가 OAM의 특성을 잘 묘사할 수 있음을 증명하였고, (그림 1b)에서 보여지는 복굴절 실린더를 이용하여 OAM의 존재를 실험을 통해서 처음으로 보였다[3].
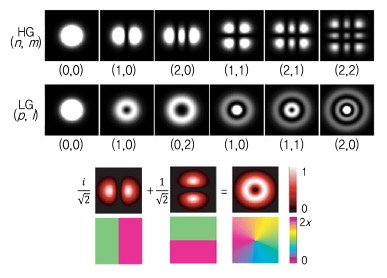
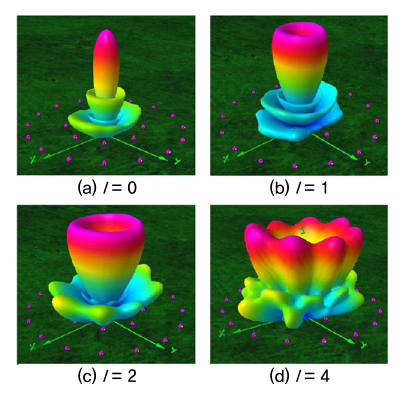
레이저 광학에서 근축 헬름홀츠(Paraxial Helmholz)방정식의 해는 카르테시안 좌표계 기반의 광 진폭 프로파일과 관련된 해(Solution)인 Hermite-Gaussian(HG) 모드와 원통형 좌표계 기반의 광 진폭 프로파일과 관련된 해인 Laguerre-Gaussian(LG) 모드로 표현될 수 있는데, Allen은 LG 모드가 궤도 각운동량의 존재를 보여줄 수 있음을 확인한 것이다. (그림 2)는 근축 헬름홀츠 방정식을 만족하는 HG 모드와 LG 모드의 다이어그램을 보여준다. LG 모드는 원통 좌표계에 대해 대칭적인 구조를 보여주고 있으며, 중심에 Vortex가 존재하고, 위상 불연속이 존재하고 있음을 확인할 수 있다.
다음 수식(2)는 LG01 모드에 대한 수식이며, (그림 2)에서 중심에 Vortex가 존재함을 확인할 수 있다.
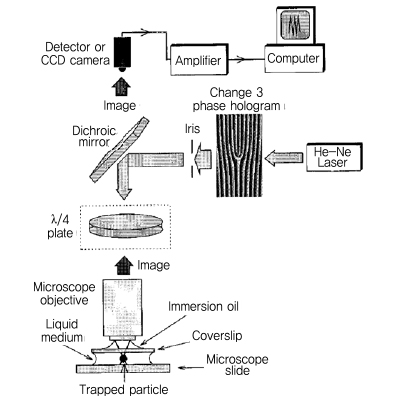
Allen이 1992년에 발표했던 논문[3]은 지금까지 약 3,300회 피인용되었다. Allen은 그 이후에도 궤도 각운동량의 존재를 실험적으로 검증한 많은 논문들을 발표하였다[5]–[9]. 특히, 강하게 입력된 레이저 신호를 이용하여 수 μm 크기의 입자를 포획하고, 포획된 입자에 미치는 힘을 측정하는 (그림 3)에서 보여지는 광 집게(Optical tweezer)[6] 및 광 스패너(Optical spanner)[7] 등의 측정 시스템을 이용함으로써 궤도 각운동량과 스핀 각운동량의 존재를 더욱 더 세밀하고 정확하게 보여주었다.
(그림 3)은 1996년 Allen이 광 각운동량을 측정하기 위해 구성한 셋업을 보여준다.
레이저에서 발생된 HG 모드는 위상 홀로그램을 통과하면서 LG 모드로 변환되고, LG 모드 레이저가 액체 매질 내부에 있는 입자를 포획한 후, 이로부터 얻어지는 영상을 컴퓨터로 기록하였다. 그 이후, 1997년 광 스패너를 이용하여 SAM과 OAM이 존재할 때, 포획된 입자의 특성 변화를 컴퓨터에 기록하였다.
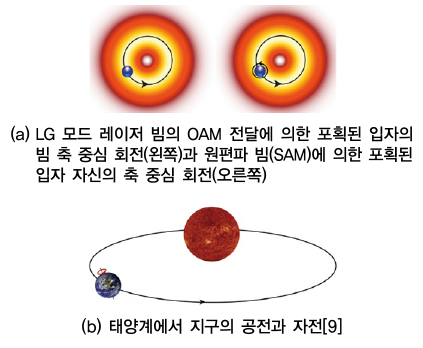
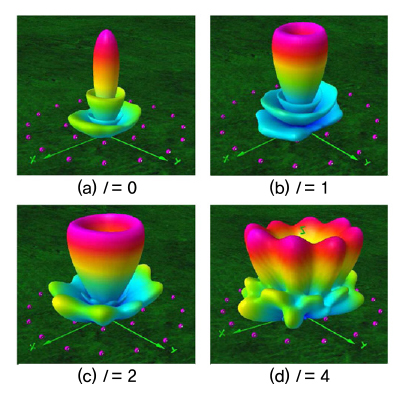
Allen은 최종적으로 (그림 4a)에서 보여지는 것처럼 광 집게 측정 셋업에서 LG 모드 레이저 빔이 포획한 입자는 LG 모드 레이저 빔 축의 궤도를 따라 원운동하는 OAM과 포획된 입자 자신의 축을 중심으로 원운동하는 SAM으로 구성됨을 밝혔다.
이는 (그림 4b)에서 보여지는 것처럼, 태양을 중심으로 지구가 공전(Revolution)하면서, 동시에 지구의 축을 중심으로 자전(Rotation)하는 형태와 유사함을 알 수 있다. 그래서 필자들은 OAM을 회전 모드(Revolution mode)라고 비유적으로 표현하였다.
2. 궤도 각운동량(OAM)의 응용
가. 광 통신
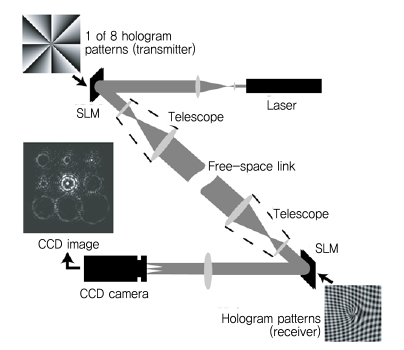
Allen과 공동으로 연구했던 Barnett 교수팀은 2004년 OAM을 통신에 응용하기 위한 실험을 수행하였다[10]. (그림 5)는 무선광(FSO: Free space optic) 시스템이며, 파면이 평면파인 레이저 신호를 헤리컬 위상을 가지는 파면인 OAM 신호로 변환하기 위해 위상 홀로그램이라는 공간 광 변조기를 사용하였다. 공간 광 변조기에서 반사된 신호는 텔레스코프를 통하여 빔 직경을 확대한 후, 자유 공간을 통하여 전송하였으며, 이를 다시 수신하여 카메라에 녹화하는 측정 셋업을 구성하였다. 실험에서 사용된 OAM은 총 8개의 모드(1=±16, ±12, ±8, ±4)를 사용하였다. Barnett 그룹은 OAM이 도청에 강한 통신 방식을 주장하기 위하여 부분적으로 신호를 검출하였을 때 나타나는 신호 열화에 대한 측정 결과도 제시하였다.
2012년 Alan 연구팀은 4개의 모드(1=±8, ±4, ±16, ±4), 그리고 각 모드별 수직 편파와 수평 편파를 이용하여, 총 8개의 states로 구성된 16QAM 변조 신호를 전송할 수 있는 Tbps급 무선광 시스템을 최초로 개발하였다[11].
또한, 2013년 동일 연구팀이 OAM 모드를 전송할 수 있는 광섬유를 제작한 후, 1.1km 전송 거리에서 총 4개의 모드(1=±1,0(좌현편파, 우현편파))를 사용하여 400Gbps를 전송하는데 성공하였다[12].
나. 전파 통신
빛은 전자파의 범주에 포함되기 때문에 동일한 전자파인 전파도 OAM이 존재해야 한다. 실제로 전파에서는 선형 편파와 더불어 SAM인 원형편파도 다양한 응용 분야에 활용되고 있다. 2007년 Thide 연구팀은 낮은 주파수에서 OAM 신호를 발생시키는 방법에 대해 발표하였다[13].
(그림 6)은 Thide 연구 그룹에서 일정한 반경의 원을 따라 특정 간격으로 배치된 배열 안테나 구조로부터 발생된 SAM과 OAM 모드의 시뮬레이션 결과를 보여주었다. 사실 SAM은 원형 편파이기 때문에 이미 다양한 전파 통신 시스템에 활용되어 왔으나, OAM은 이론적으로 증명된 사례가 없었기 때문에 전파 OAM 분야 활용을 위한 원리를 보여주었다는 것에서 의의를 찾을 수 있다[13].
그 이후, 논문에서 제시된 결과에 대한 정확성에 의문점들이 많았기 때문에 Thide 연구 그룹은 실제 측정하고 평가하여 전파 영역에서도 OAM을 발생 시킬 수 있음을 실험적으로 확인하였고, 주파수 2.4GHz, 전송 거리 442m에서 0과 1모드를 이용하여 다중 전송이 가능함을 보였다[14].
다. 이미징
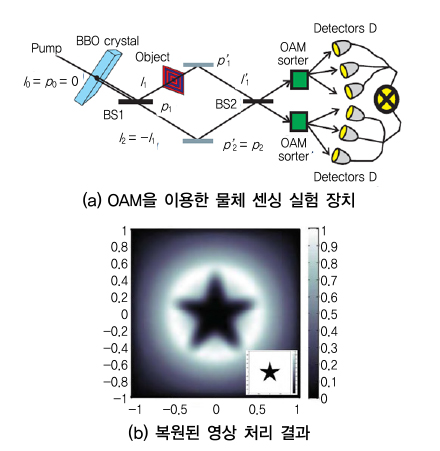
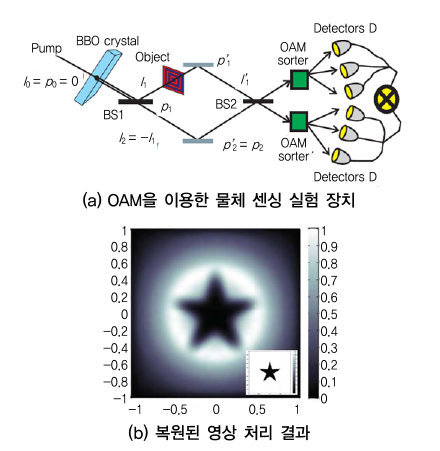
2015년 A.V. Sergienko 연구팀은 OAM 모드를 이용하여 물체를 영상화하고, 인식 CSI(Correlated spiral imaging)이라는 영상 기법을 개발하였다[15]. CSI 기술은 특히 OAM 모드의 대칭성을 이용하기 때문에 적은 측정 데이터를 이용하여 영상화할 수 있음을 보였고, 위상 영상화 기법에서 OAM 모드의 사용은 영상의 Edge 구분 성능을 개선하는 효과를 얻을 수 있음을 보였다.
(그림 7)은 A.V.Sergienko 연구팀이 OAM을 이용하여 물체를 센싱하는 실험 셋업과 실제 이미지에 대한 복원된 영상 결과도 보여준다[15].
OAM 모드를 영상 복원에 사용함으로써 얻어질 수 있는 특별한 장점이 있다. OAM 모드의 파면이 헤리칼 구조로 변하면서 진폭 특성이 대칭을 이루기 때문에 방위각을 중심으로 물체가 회전하는 경우, 물체의 회전 특성에 영향을 받지 않고 영상 복원이 가능하다는 것이다. (그림 7b)의 별 모양의 물체가 회전하더라도 복원된 영상은 별 모양을 유지할 수 있음을 연구팀은 보여주었다. 추가적으로, 바이오 분야에서 세포가 사멸할 경우, 셀의 대칭성이 깨지고, 대칭 분포의 변화는 암세포를 의미할 가능성이 있음을 확인하는 응용 분야를 제안하였다[15].
2013년 Miles. J. Padgett 연구팀은 OAM 신호를 회전하는 물체에 입사한 후, 반사된 신호로부터 추출된 도플러 시프트 주파수로부터 회전체의 속도를 검출하는 논문을 발표하였다 [16]. 연구팀은 가능한 응용 분야로 후방 산란된 빛에서 회오리의 원격 센싱 및 우주의 회전체로부터의 원격 센싱 등을 제안하였다.
2014년 Liu 연구팀은 OAM을 MIMO(Multi-in-multi-out) 레이다와 MISO(Multi-in-single-out) 레이다에 적용한 연구 결과를 발표하였다[17]. 고전적인 레이다는 평면파를 이용하였지만, OAM을 이용한 레이다는 파면이 헤리칼 프로파일로 계속 변화하기 때문에 레이다 목표물의 방위각 정보를 얻는 것이 가능함을 보였다.
라. 음파
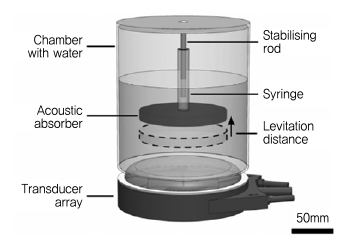
Allen이 광파(Photon)에서 OAM의 실험적 증명과 활용 분야에 대한 연구를 발표했지만, 음파에서도 OAM의 실험적 증명에 대한 연구가 이루어졌다. Demore는 2012년 (그림 8)에서 보여지는 것처럼, 음파(Phonon)에서 발생하는 OAM의 양을 실험적으로 측정하였다[18].
실험 셋업은 투명 챔버, 음파 흡수체, 배열 기반 빔 발생기, 공기 방울이 제거된 액체, 그리고 음파 흡수체 지지 라인으로 구성되었다. 음파 흡수체는 직경 100mm, 두께 10mm, 무게 87g인 재질을 사용하였으며, 배열 기반 음파 발생기의 주파수는 550kHz, 1,000개의 엘리먼트가 각각 정해진 위상 천이된 신호로 구동되는 고출력 음파를 발생한다.
포톤(Photon)과 달리, 포논(Phonon)은 편파가 없기 때문에 SAM을 가지고 있지 않으므로 음파 흡수체를 부양하는 힘과 회전시키는 힘의 비율로부터 OAM의 양을 바로 도출해 낼 수 있음을 실험을 통해서 증명하였다.
마. 궤도 각운동량 활용을 위한 극복 기술
OAM은 이론적으로 무한개의 직교 모드를 가지고 있다는 것이 증명되었으나, 아직 다음과 같은 몇가지 제약 사항 때문에 OAM의 활용 분야는 매우 제한적이다.
• 빔의 퍼짐 현상으로 인해 발생하는 수신부 안테나의 크기 증가 및 이로 인한 송수신간 거리 제약
• 다중 산란 환경에서의 모드 직교성 깨짐 현상
• 모드 발생시 모드간 cross-talk 문제
• 모드의 좁은 대역폭
따라서 위에서 열거된 문제점들을 극복하는 기술 개발이 매우 필요하다고 할 수 있다.
Ⅱ. 전파 궤도 각운동량 모드 발생 기술 동향
일반적으로 회전 모드를 발생하는 방식에는 3가지 전통적 방식이 있으며, 최근에는 좀더 실용적으로 전파 궤도 각운동량 모드를 발생하는 방법에 대한 논문들이 발표되었다[19]–[29].
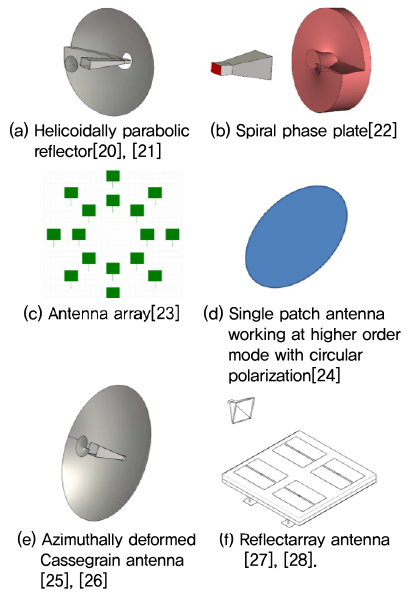
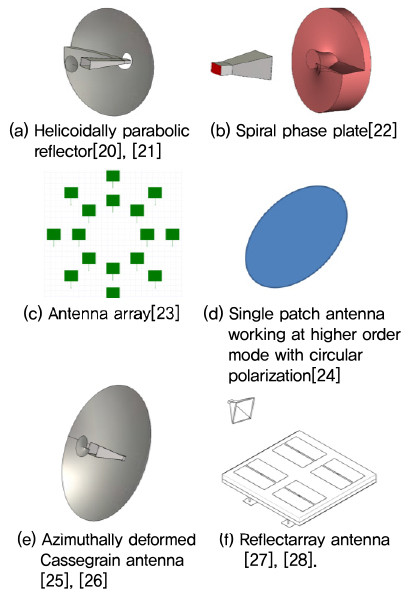
(그림 9a)는 전자파의 반사 특성을 이용하는 것으로 혼 급전부의 신호가 단차가 있는 포물면 반사판으로부터 반사되면 전파 궤도 각운동량 모드가 발생한다. 주반사판은 1=h/2λ의 단차를 가지며 포물면 특성에 의해 안테나 이득을 높일 수 있다[20], [21].
(그림 9b)는 유전체 렌즈에 단차를 형성시켜 회전 모드를 발생하는 방식이다. φ에 비례하여 두께가 변하는 나선형 위상판(Spiral phase plate)으로 1=1(n–1)·h/λ 정수이면 각운동량이 없는 일반적인 헤르밋-가우시안(Hermit-Gaussian) 모드가 투과후 e-ilφ의 위상항을 가지는 라게르-가우시안 모드로 바뀐다.
여기서 n은 위상판의 굴절률로서 그림에서 위상판 단차의 바로 윗부분은 1·h의 광경로를 지나는 반면, 단차의 바로 아랫부분은 n·h인 광경로를 지나게 된다[22].
(그림 9c)는 원형 궤적을 따라 N개의 패치로 이루어진 균일 원형 배열 안테나(Uniform circular array antenna)이다[23]. 하나의 원주를 따라 배치된 패치들이 하나의 전파 궤도 각운동량 모드 발생기로 동작하며, i 번째 패치는 i·θ만큼 지연된 전기신호에 의해 구동된다. θ=2πl⁄N 일 때 각운동량 l인 전파 궤도 각운동량 모드가 발생하는데, 각 안테나 소자 개수가 8개일 때 l=1인 회전 모드를 발생시키기 위하여 θ=2π⁄8씩 순차적으로 증가하는 값을 가지도록 신호를 급전한다. 이와 같은 급전법에는 버틀러 매트릭스, 로트만(Rotman) 렌즈 등을 이용할 수 있다[24].
(그림 9d)는 단일 급전 타원형 패치안테나이다. 이 안테나는 원형 구조에 타원이라는 비대칭을 형태를 만듦으로써 원형 편파를 발생시킨다. 특히, 고조파 모드에서 발생하는 TMnm 모드는 Ex와 Ey가 대략 e-i(n-1)φ 에 비례하므로 n-1 전파 궤도 각운동량 모드가 생성된다[25].
(그림 9e)는 (그림 9a)와 유사하지만 주반사판 대신 부반사판에 단차를 주어 전파 궤도 각운동량 모드를 발생시킬 수 있다. 이 구조는 제작이 간단할 뿐만 아니라 혼 급전부의 신호가 부반사판에 반사되면 원하는 전파 궤도 각운동량 모드 신호로 바뀌게 되며, 급전 안테나로 후방 반사되는 신호의 영향이 줄어들기 때문에 안테나의 반사 특성이 개선된다[26], [27].
(그림 9f)는 곡면 반사체를 부피가 작은 반사 배열(Reflectarray) 방식으로 변형한 반사판을 이용하여 전파 궤도 각운동량 모드를 발생하는 구조이다. 반사 배열을 구성하는 각 단위 소자에 스위칭 소자를 추가함으로써 하나의 반사 배열 안테나에서 원하는 다른 전파 궤도 각운동량 모드를 발생시킬 수 있는 장점이 있다[28], [29].
Ⅲ. MIMO와 전파 궤도 각운동량 비교
MIMO(Multiple-input multiple output) 통신 시스템과 전파 궤도 각운동량 모드 통신 시스템은 모두 MIMO Channel이라는 Air interface를 형성하여 송수신하는 공통점이 있다. 따라서 두 시스템은 정보이론 관점에서 동일한 표현식으로 나타낼 수 있어 유사한 통신 시스템으로 보일 수도 있다. 이에 2012년 Ove Edfor 등은 논문에서 OAM이 MIMO에 비해 새로운 개념이 아니라고 주장했다[30].
하지만 MIMO 통신 시스템과 전파 궤도 각운동량 모드 통신 시스템은 구현상의 차이점을 가지며, 이 차이로 인해 두 시스템은 특성 및 값이 서로 다른 MIMO channel을 형성하게 된다. 즉, 송수신기간 무선 채널 행렬의 특성 및 값에 차이가 발생하게 된다. 두 시스템간의 상이한 MIMO 채널은 두 시스템간 상이한 성능 및 특성을 갖게 하며, 운용환경 및 시나리오에 따라 더 적합한 시스템이 결정된다. 두 시스템의 유사점과 차이점을 보다 자세히 살펴보자.
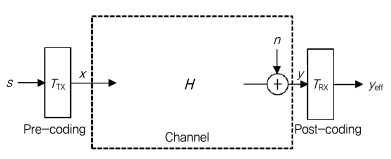
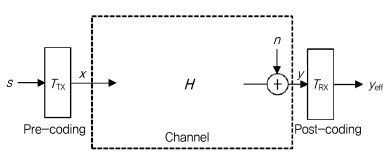
MIMO 시스템과 전파 궤도 각운동량 모드 시스템은 (그림 10)과 같이 MIMO 채널을 갖는 시스템으로 동일하게 표현할 수 있어, 두 시스템이 매우 유사해 보일 수 있다.
변조신호벡터 s=[s1 s2 s3]T가 프로코딩 TTx를 거쳐 송신신호벡터 x로 전환되어 전송되면, 수신단은 수신신호벡터 y를 포스트코딩 TRx를 거쳐 yeff를 얻는다. 이때, H는 송수신기간의 채널계수 행렬이며, n은 수신기에서의 백색잡음 벡터이다. 두 시스템의 송수신 신호를 수식으로 표현하면 (3)과 같이 동일하게 나타낼 수 있다.
MIMO 시스템에서는 TTx와 TRx 연산이 송수신기의 기저대역에서 수행되며, 전파 궤도 각운동량 모드 시스템에서는 RF 회로 및 송수신 안테나에서 수행되는 구현상의 차이점을 갖는다. 이러한 구현상의 차이는 MIMO 시스템의 채널 H와 전파 궤도 각운동량 모드 시스템의 채널 H가 다른 특성을 갖도록 하며, 두 시스템은 상이한 성능 및 특성을 갖는다.
MIMO 통신 시스템은 순시 MIMO 채널에 적응적인 시스템이며, 전파 궤도 각운동량 모드 시스템은 자신의 순시 MIMO 채널 H 의 상태의 변화를 반영하지 않는 고정적 시스템이라는 차이가 있다. 즉, 전파 궤도 각운동량 모드 시스템은 TTx와 TRx가 미리 정해져 있고, 변경하지 않는 환경에서의 운용을 목적으로 한다. 따라서 전파 궤도 각운동량 모드는 채널이 변하지 않는 H가 Deterministic한 환경에 적합한 시스템이다. 반면 MIMO 시스템은 H가 변하는 환경에서의 운용을 목적으로 한다. H가 변하는 환경에서 순시 H값을 추정하여 TTx와 TRx를 적응적으로 결정한다. 전파 궤도 각운동량 모드 시스템은 TTx와 TRx를 운용 환경에 맞게 미리 결정하여 다른 환경에서 사용하기에는 어려운 단점이 있으나, 기저대역에서의 수신 신호 분리를 위한 신호처리를 필요로 하지 않아 MIMO 시스템 대비 낮은 가격의 시스템 구현이 가능한 장점을 갖는다. 또한 전파 궤도 각운동량 모드 시스템의 기저대역에서 신호처리를 필요로 하지 않는 특성은 고속의 데이터 송수신을 용이하게 한다.
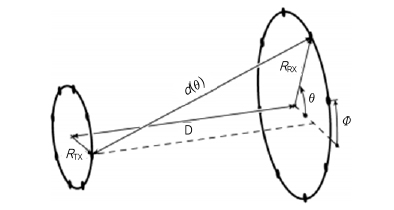
전파 궤도 각운동량 모드 시스템을 UCA(uniform circular arrays)형태로 구현 할 경우, (그림 11)과 같이 두 시스템간의 TTx와 TRx 가 매우 비슷한 형태를 갖는다[31]. 따라서 신호처리 가격문제만 해결된다면 MIMO 시스템이 전파 궤도 각운동량 모드 시스템보다 일반적으로 더 유연하고 좋은 성능을 갖는다는 잘못된 결론을 내릴 수도 있다. MIMO 시스템 및 전파 궤도 각운동량 모드 시스템에서 MIMO 채널 H 는 시스템의 RF 회로 및 안테나 등에 의해서 영향을 받는다. MIMO 시스템의 RF 회로 및 안테나 등은 주로 페이딩 채널 환경에 적합하게 설계되었다. 반면, 전파 궤도 각운동량 모드 시스템은 LOS(Line-of-sight) 환경에 적합한 RF 회로 및 안테나 구조를 갖는다. 따라서 두 시스템이 갖는 각각의 MIMO 채널은 같은 환경에서 다른 특성 및 값을 갖게 된다. 두 시스템간의 MIMO 채널 H의 차이는 전파 궤도 각운동량 모드 시스템이 전파 궤도 각운동량 모드 발생을 UCA가 아닌 다른 방식으로 구현하였을 경우 더욱 분명해 진다. 예를 들어 전파 궤도 각운동량 모드 신호를 카세그레인 반사판 안테나를 사용하여 발생하는 시스템은 높은 송수신 안테나 이득을 갖도록 시스템을 설계하는 것이 가능하므로 기존 MIMO 시스템의 MIMO 채널보다 좋은 H 특성을 갖는다.
Ⅳ. 결론
본고에서는 전파 궤도 각운동량 연구의 역사와 원리 및 개념에 대해 정리하였다. 또한 최근에 발표된 연구 결과들을 중심으로 전파 궤도 각운동량 모드의 활용 분야에 대해서도 살펴 보았다. 하지만, 전파 궤도 각운동량 모드는 송수신 거리가 증가함에 따라 안테나 크기도 커지는 문제가 있기 때문에 아직 실용화하는데 한계가 있다. 또한 MIMO 대비 장점이 있는가에 대한 의구심들이 많기 때문에 지금까지의 연구는 전파 궤도 각운동량 모드 발생 기술, 근거리 통신 기술 등에 국한되었다. 그러므로 전파 궤도 각운동량 모드의 실용화 기술 연구는 매우 의미 있다고 할 수 있다.
References

(그림 1)
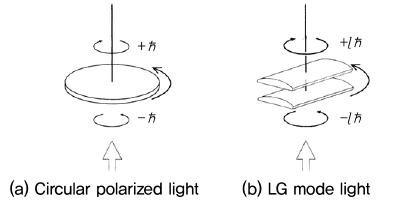
각운동량 관찰 개념도<a href="#r003">[3]</a>
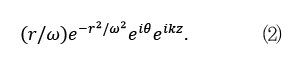
(그림 2)
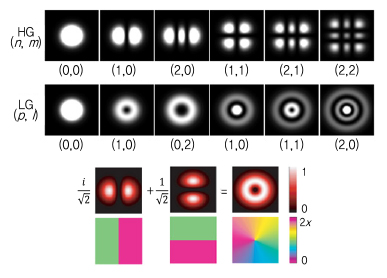
근축 헬름홀츠 방정식의 해인 HG 모드와 LG 모드<a href="#r004">[4]</a>
(그림 3)
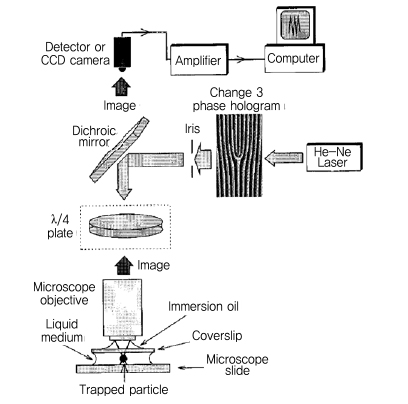
광 각운동량을 관찰하기 위한 광 집게 측정 셋업<a href="#r006">[6]</a>
(그림 4)

광 집게 측정 셋업을 통하여 포획된 입자의 원운동과 지구의 공·자전
(그림 5)
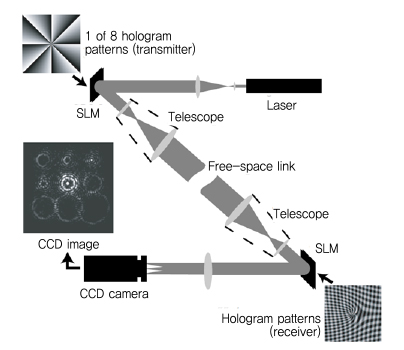
OAM 무선광 통신 응용 실험 블록도<a href="#r010">[10]</a>
(그림 6)
원형 배치된 배열 안테나에 의해 발생된 OAM 모드<a href="#r013">[13]</a>
(그림 7)
OAM을 이용한 물체 센싱 실험 셋업<a href="#r015">[15]</a>
(그림 8)

음파 OAM 측정 셋업<a href="#r018">[18]</a>
(그림 9)
전파 궤도 각운동량 모드 발생 구조
(그림 10)
전파 궤도 각운동량 모드 송수신 시스템
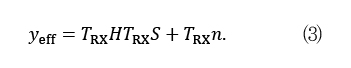
(그림 11)
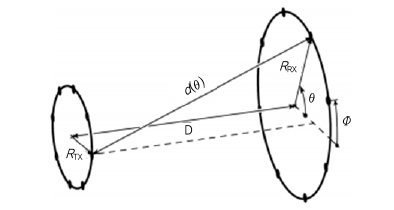
UCA 송수신 시스템<a href="#r031">[31]</a>