양자컴퓨팅 기술 연구개발 동향
R&D Status of Quantum Computing Technology
- 저자
-
백충헌양자창의연구실 CHBaek@etri.re.kr 황용수양자창의연구실 yhwang@etri.re.kr 김태완양자창의연구실 TaewanKim@etri.re.kr 최병수양자창의연구실 bschoi3@etri.re.kr
- 권호
- 33권 1호 (통권 169)
- 논문구분
- 4차 산업혁명 사회의 초연결 지능과 신뢰 인터넷 기술 특집
- 페이지
- 20-33
- 발행일자
- 2018.02.01
- DOI
- 10.22648/ETRI.2018.J.330103
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- The calculation speed of quantum computing is expected to outperform that of existing supercomputers with regard to certain problems such as secure computing, optimization problems, searching, and quantum chemistry. Many companies such as Google and IBM have been trying to make 50 superconducting qubits, which is expected to demonstrate quantum supremacy and those quantum computers are more advantageous in computing power than classical computers. However, quantum computers are expected to be applicable to solving real-world problems with superior computing power. This will require large scale quantum computing with many more qubits than the current 50 qubits available. To realize this, first, quantum error correction codes are required to be capable of computing within a sufficient amount of time with tolerable accuracy. Next, a compiler is required for the qubits encoded by quantum error correction codes to perform quantum operations. A large-scale quantum computer is therefore predicted to be composed of three essential components: a programming environment, layout mapping of qubits, and quantum processors. These components analyze how many numbers of qubits are needed, how accurate the qubit operations are, and where they are placed and operated. In this paper, recent progress on large-scale quantum computing and the relation of their components will be introduced.
Share
Ⅰ. 서론
양자컴퓨터는 1982년 리처드 파인만이 양자 시스템에 대한 시뮬레이션 장비로서 그 가능성과 필요성을 처음 제시하였다[1]. 이후 도이치 알고리즘[2], 쇼어 알고리즘[3]이 알려지면서 알고리즘 레벨에서 양자컴퓨터가 비트 기반 슈퍼컴퓨터보다 더 빨리 계산할 수 있다는 가능성이 대두되었다. 양자컴퓨터는 양자 비트, 즉 큐비트(Qubit: quantum bit)를 이용하여 정보를 처리한다. 큐비트는, 0과 1 이분법적으로 표현 가능한 비트와는 달리, 양자역학적 0과 1 상태로 기술된다. 정보 표현방식이 비트에서 큐비트로 바뀌게 되면, ICT 전반에서 정보처리과정의 근본적인 변화가 필요하다.
양자컴퓨터를 구성하는 큐비트의 수가 선형적으로 늘어날수록, 양자컴퓨터가 처리 가능한 정보의 양은 지수적으로 늘어난다. 미세한 나노 공정 기술이 발전함에 따라 다양한 물질과 시스템을 이용하여 큐비트가 구현되었다. 실험적으로 구현된 큐비트의 수가 늘어나면서, 고전 컴퓨터보다 더 빠른 연산 수행이 정말 가능한 지 그 기대가 커지고 있다. 특히, 최근에는 Google에서 초전도 큐비트 기반의 양자컴퓨터용 양자 화학 시뮬레이션 모델을 제시하였고[4], IBM에서 BeH2 등의 더 큰 분자의 에너지 상태를 양자컴퓨터를 이용하여 시뮬레이션 하였다[5].
최근 Google, IBM, Microsoft, Intel 등에서 경쟁적으로 양자컴퓨터 칩에 대한 연구개발 결과를 공개하고 있다. 양자컴퓨터의 계산 성능과 고전 컴퓨팅의 한계에 대한 비교를 명확히 확인하고자 하는 실험(Proof of quantum computational advantage, quantum supremacy)들이 진행되고 있다. 이에 따라서, 일정 숫자 이상(대략 50큐비트)의 큐비트로 신뢰도가 높은 연산을 수행하며, 연산 대상이 되는 문제의 크기가 고전 컴퓨터의 한계를 넘어서는 상황에 거의 도달하였다고 볼 수 있다.
양자컴퓨팅 파워가 점점 늘어나면, 양자 화학뿐만 아니라 최적화 문제, 검색, 머신 러닝, 보안 컴퓨팅 등에 널리 사용될 수 있다. 그러나 대규모 양자컴퓨팅을 위하여는 여기서 한발 더 나아가야 한다. 양자컴퓨팅의 정확도를 더 높여야 하고(신뢰성 향상), 더 많은 수의 큐비트를 이용해야 하며(확장성 향상), 다양한 알고리즘을 다루어야 한다(범용성 향상). 최근에는 관련 연구가 광범위하게 진행되므로 과거의 예상보다는 이른 시점에 양자 슈퍼컴퓨팅이 구현될 것으로 기대된다.
본고에서는 양자컴퓨팅의 최근 연구개발 동향을 살펴보고 향후 진행해야 하는 주요 이슈들을 살펴본다. Ⅱ장에서는 양자컴퓨팅의 기본적 동작원리를 설명한다. Ⅲ장에서는 양자컴퓨팅을 실제로 프로그래밍하고 이를 기계어 수준으로 분해하는 과정을 설명한다. Ⅳ장에서는 이러한 기계어를 양자 프로세서에 대응시키는 시스템의 합성 및 운영 과정에 대하여 설명한다. Ⅴ장에서는 양자컴퓨터의 양자 프로세서 동향을 살펴본다. Ⅵ장에서는 향후 진행해야 할 연구개발 내용을 고찰하고 본고를 마무리한다.
Ⅱ. 양자컴퓨팅의 동작 원리
1. 사용되는 양자역학 원리
가. 양자 중첩 현상
양자역학에서 물질의 상태는 힐버트 공간에서의 벡터형태로 표현된다. 간단하게는 여러 기저 상태들의 선형 결합으로 양자 상태를 표현한다. 큐비트는 두 개의 직교하는 기저 상태로 표현하는 양자 상태인데, 비트와 큐비트의 차이는 양자 상태의 특징에서 기인한다. 고전 정보는 0 또는 1의 상태를 갖지만, 양자 상태는 0과 1의 선형 결합, 즉 중첩 현상으로 정보를 표현한다. 동일한 N 개의 비트 혹은 큐비트가 있다면, 비트는 반드시 2N개 조합 중 한 개의 값을 선택해야 하지만, 큐비트는 이들의 중첩까지 포함하여 하나의 양자 상태로 표현할 수 있다.
양자컴퓨팅이 강점을 발휘하는 부분은 중첩을 이용한 특징에서 나온다. 예컨대 수많은 경우의 수 중에서 가장 좋은 경우가 어떤 경우인지 계산해본다고 하자. 이때 기존 컴퓨터는 모든 조합을 순차적으로 계산하여 가장 좋은 결과를 산출하지만, 양자컴퓨터는 모든 조합을 동시에 다루기 때문에 비유적으로는 이를 동시에 계산한다고 생각할 수 있다. 이러한 특징 때문에 양자 병렬처리라고 불리기도 한다. 따라서 특정 문제는 양자컴퓨터는 양자 병렬 처리를 이용하여 기존의 컴퓨터보다 더 빠르게 계산할 수 있다.
나. 관측 붕괴 현상
양자 정보는 관측 때문에 양자 상태가 바뀔 수 있다. 이는 우리가 고전적으로 생각하는 관측과 다른 중요한 특징이다. 동전을 상자 안에 넣어 앞면인지 뒷면인지 그 확인할 때 동전의 상태는 미리 정해져 있으며 우리는 이를 확인할 뿐이다. 그리고 동전이 많으면 많을수록 그 확률은 앞면과 뒷면 50%로 수렴하게 된다. 그러나 양자 상태는 대상의 상태가 미리 정해져 있지 않을 수 있다. 따라서 고전적 관측과 달리 관측 때문에 대상의 양자 상태가 바뀐다. 큐비트의 상태가 0과 1의 절반의 확률로 중첩되었을 때, 측정하게 되면 중첩상태는 그 즉시 사라져 0 또는 1로 큐비트의 상태가 변하게 된다. 이는 고전적인 확률과 다른 중요한 부분이다. 이런 큐비트 상태는 0인 큐비트가 절반, 1인 큐비트가 절반이 있어 0과 1 상태가 반반으로 나오는 확률과는 다른 경우이다. 0과 1의 중첩 상태인 큐비트를 다수 준비하여 결과적으로 0과 1 상태가 반반이 나오더라도, 같은 결과를 도출할 뿐 큐비트의 상태는 다르다.
한편, 양자 상태의 붕괴는 비가역적이어서 측정한 뒤 다시 원래의 양자 상태로 돌아가지 못한다. ICT 측면에서 관측 붕괴 현상은 외부 측정을 원천적으로 방지하므로 정보의 보안성을 보장해준다.
관측 붕괴 현상과 중첩 현상에 따라 양자 정보는 복제 불가능하다. 이 때문에, 양자 정보에 오류가 생겼을 때 복사를 통해 정보의 오류를 고치는 방법이 불가능하다. 따라서 양자 정보의 오류를 고치는 것은 별도의 보조적 큐비트를 이용해 기존의 양자 정보를 바꾸지 않으면서 오류 여부를 파악해야 한다.
다. 양자 얽힘 현상
양자 얽힘 현상은 둘 이상의 양자 상태가 서로 의존적인 상태를 말한다. 예컨대, 두 큐비트의 상태가 01과 10인 상태를 중첩되었다고 하자. 이 경우 첫 번째 큐비트 상태가 0이면 두 번째 큐비트의 상태는 반드시 1이고, 반대로 첫 번째 큐비트 상태가 1이면 두 번째 큐비트의 상태는 반드시 0이 된다. 또한, 첫 번째 큐비트의 상태가 0이거나 1일 확률은 양자 중첩현상에 따라 표현이 된다. 이에 따라 첫 번째 큐비트의 상태 결정에 따라 의존적으로 두 번째 큐비트의 상태가 결정되기 때문에 이를 양자 얽힘 현상이라고 한다.
양자 얽힘 현상은 비국지적 현상으로 공간적으로 아주 멀리 떨어져 있어도 나타날 수 있다. 얽혀있는 두 큐비트를 아주 멀리 떨어뜨리고 첫 번째 큐비트를 측정한다면 두 번째 큐비트는 이에 즉각적으로 양자 상태가 변한다. ICT 측면에서, 정보가 순간적으로 전달되는 것은 아니다. 얽힘 현상에 대한 양자 상태 변화는 즉각적이나 정보의 전달은 빛의 속도로 한계가 생긴다. 얽힘 현상은 통신이나 계산과정에서의 관계를 유지하게 하여 공간적으로 떨어져 있는 정보 간에 간섭 현상이 나타나도록 한다.
2. 양자컴퓨팅의 높은 계산성능 원리
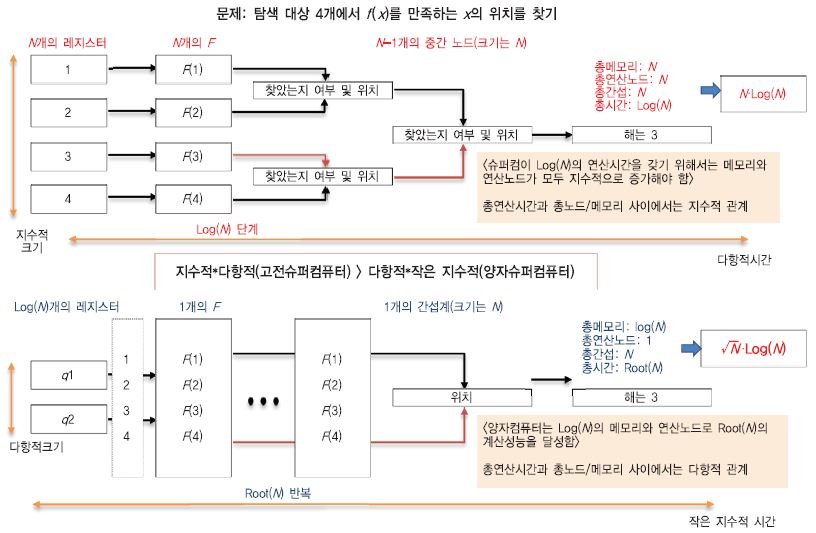
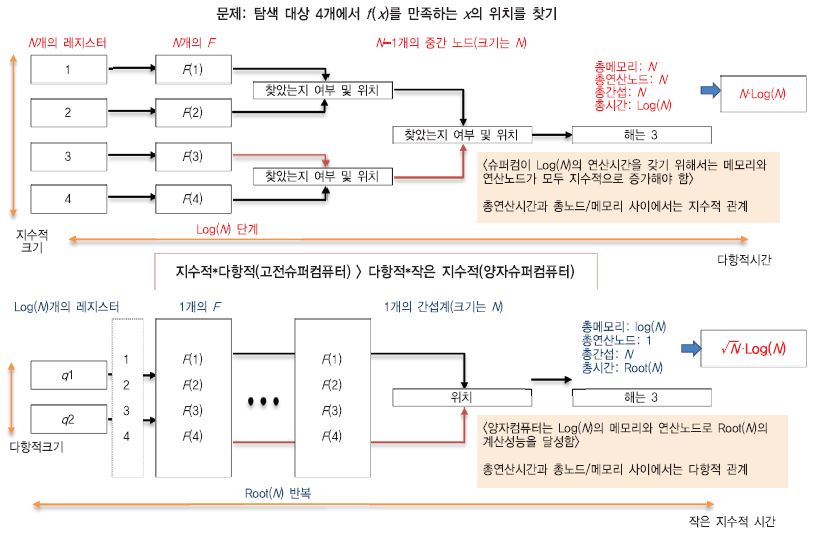
양자 중첩 현상과 양자 얽힘 현상에 따라 양자컴퓨터는 기존의 비트기반 고성능 병렬컴퓨팅에 비교해서 높은 계산 성능을 가질 수 있다. 이를 조금 더 구체적으로 설명하면 다음과 같다. (그림 1)에서는, N개의 탐색공간에서 주어진 함수 F를 만족하는 해를 찾는 과정에 대하여 고전슈퍼컴퓨터와 양자슈퍼컴퓨터의 동작 과정의 차이를 개념적으로 보여준다. 고전슈퍼컴퓨터에서 계산시간 측면에서 초고속 연산을 하기 위해서는 탐색공간 N에 해당하는 만큼 많은 수의 연산 노드를 사용해야 하고, 그러한 노드들로부터 해를 갖는 노드 정보를 추출하기 위한 단계를 거친다. 이때, 최대한 많은 연산 노드를 사용하고, 중간 추출 노드를 사용한다고 가정하면, 전체 연산시간은 log(N) 정도가 된다. 하지만, 이 경우 필요한 자원 요구량은 N개의 연산 노드와 중간 노드들이므로 전체적으로는 O(N)개의 노드가 필요하다. 필요한 시간과 공간을 모두 고려한 자원 요구량은 따라서 O(N·logN)이 된다. 반면, 양자컴퓨터의 경우에는 필요한 공간 측면에서 O(logN) 정도의 큐비트와 1개의 연산 노드이면 된다. 따라서, 공간복잡도는 0(logN)이다. 시간복잡도는 양자알고리즘의 단계 수인데, 이러한 문제의 경우에는 0(√N)이라는 것이 증명되어 있다. 따라서, 전체 복잡도는 0(logN·√N) 정도가 된다. 결과적으로, 시간 및 공간복잡도를 모두 고려하면, 양자슈퍼컴퓨터가 0(√N) 정도 작다는 것을 알 수 있다. 이러한 차이는 N의 크기에 비례하므로, 양자컴퓨터의 실질적인 성능향상 효과는 입력 크기 혹은 문제의 크기가 커질수록 증가함을 알 수 있다.
3. Quantum Technology Readiness Level(QTRL)
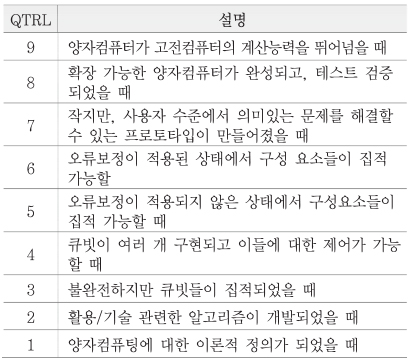
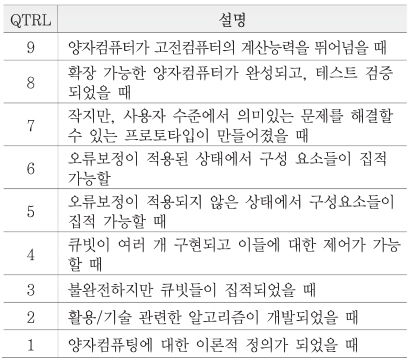
연구개발 과정에서 주로 사용되는 기술 수준 지표로 TRL(Technology Readiness Level, 기술성숙도)을 사용한다. 미국 NASA에서 우주산업의 기술투자 위험도 관리의 목적으로 1989년 도입하였다. 이러한 기준에 따라서, 양자컴퓨팅 관련 TRL을 고려할 수 있는데, 현재 이와 관련하여 양자컴퓨팅 맞춤형 TRL이 <표 1>과 같이 제안되었다[6]. 현재 이 지표에 기술된 내용은 통상적인 TRL과는 다르게 양자컴퓨팅이 개념적 설계 단계부터 고전슈퍼컴퓨팅을 뛰어넘는 수준을 최종수준으로 하여 단계가 구분되어 있다. 본 자료에서는 양자컴퓨팅의 세부기술을 QTRL을 기준으로 정리하였다.
Ⅲ. 양자컴퓨터 프로그래밍 기술 동향
1. 개념
양자컴퓨터 프로그래밍 환경은 양자 프로그래밍 언어로 표현된 양자알고리즘을 컴파일 하는 컴파일러와 양자컴퓨팅을 시뮬레이션하는 가상 양자머신을 포함한다. 양자컴파일 과정은, 사용자가 작성한 상위수준의 양자알고리즘을 양자컴퓨팅에서 주로 사용되는 간단한 기본 게이트의 집합으로 분해하는 과정을 의미한다. 이 과정에서 사용되는 기본 게이트는 두 개 큐비트 형태의 게이트인 CNOT 게이트와 단일 큐비트 게이트들로 구성된다.
양자컴퓨팅을 가장 간단하게 실행하는 방법으로, 사용자가 작성한 상위수준 언어를 CNOT 게이트와 임의의 단일 큐비트 게이트로 컴파일하는 방법을 고려할 수 있다. 하지만 이때 양자 게이트와 큐비트에서 약간의 오류가 발생하는 경우에도, 양자회로 전체에서의 연산결과 정확도가 크게 낮아지는 문제점이 발생한다. 따라서 이러한 접근은 주로 상대적으로 작은 크기의 문제를 대상으로 한다. 반면 상대적으로 양자회로가 큰 경우에는, 게이트와 큐비트에서의 오류에도 불구하고 신뢰도가 높은 연산결과 도출을 위해서 오류보정 및 결함허용 방식[7]을 적용한다. 이에 따라서, 오류보정 및 결함허용적으로 구현 가능한 게이트의 집합으로 분해되어야 한다. 이때 주로 사용되는 게이트의 조합은 CNOT, H, T 게이트 등이다. 컴파일 결과로 나타나는 양자 어셈블리(Quantum ASseMbly) 코드는 흔히 QASM이라고 불리며, CNOT, H, T 게이트 등으로 표현된다.
가상 양자머신은 양자컴퓨팅을 시뮬레이션하는 비트기반 컴퓨터를 말한다. 여기서 양자컴퓨팅의 시뮬레이션은 양자 레지스터, 양자 상태 초기화, 양자 연산, 양자 측정 등을 포함한다. n개 큐비트 레지스터는 2n개의 양자상태의 중첩으로 표현된다. 따라서 30큐비트 레지스터를 위해서는 230개의 양자 상태의 중첩을 표현해야 하므로 약 17GB 정도의 메모리를 사용할 수 있는 컴퓨터가 필요하며, 40큐비트 레지스터를 위해서는 17TB 정도의 컴퓨터가 필요하다.
이러한 가상 양자머신을 이용하여 양자알고리즘을 슈퍼컴퓨터에서 실행하여 봄으로써, 양자알고리즘의 실행 결과를 계산해 볼 수 있다. 그러한 과정에서 양자알고리즘이 정확하게 작성되었는지를 검증할 수 있으며, 양자알고리즘의 컴파일 과정에서 발생할 수 있는 오류도 발견할 수 있다. 혹은 이상적인 양자컴퓨팅 환경 이외에 실제 환경에서 양자컴퓨터가 받는 물리적 환경으로 인한 오류의 영향을 모델링 하고 이를 분석하여, 양자컴퓨터를 설계하는 데에도 사용할 수 있다.
2. 기술개발 동향
양자 프로그래밍 언어가 처음으로 소개된 것은 1998년 Ömer에 의한 QCL(Quantum Computation Language) 이다[8]. 이는 C++언어 기반의 양자 프로그래밍 언어이다. 이후 이는 Sanders와 Zuliani[9], Bettelli[10] 등에 의하여 더욱 발전되었다. 양자 프로그래밍 환경에 대한 연구는 2012년을 기점으로 급격히 발전하기 시작하였다. 큰 규모의 양자회로를 프로그래밍하고 컴파일 하기 위해 Haskell 언어를 기반으로 한 Quipper: A Scalable Quantum Programming Language[11]가 소개되었으며, C언어를 기반으로 하는 컴파일러 시스템 ScaffCC도 소개되었다[12]. ScaffCC는 양자 어셈블리 코드인 QASM을 순차적으로 나열하는 방식인 QASMF(Flattened QASM) 이외에도 컴파일 결과를 계층적으로 나타내는 QASMH(Hierarchical QASM) 방식을 제안함으로써, 컴파일 결과의 크기를 크게 줄일 수 있으며, 컴파일 수준에서의 자원 분석 기능이 포함되어 있다.
현재 ScaffCC 컴파일 결과에 대한 검증 도구로는 회로 길이가 너무 길지 않은 30큐비트 이하의 양자알고리즘에 대하여, QX simulator[13]가 연결되어 사용될 수 있다. 최근 구글에서는 신약 개발에 활용될 수 있는 양자화학 분야에서 필요한 패키지 Open Fermion을 발표하였다[14]. 이러한 패키지는 스위스 ETH Zürich 대학에서 만든 양자컴퓨터 프로그래밍 환경인 Project Q나 Rigetti Computing에서 만든 양자컴퓨터 프로그래밍 환경인 Forest를 연동해서 실행할 수 있다. 2014년 마이크로소프트의 QuArc(Quantum Architecture and Computation) 팀은 F# 기반의 LIQUi|> 프로그램을 개발하여, 사용자가 20~30개 큐비트 규모까지의 양자알고리즘을 프로그래밍하고 이를 가상 머신을 통해 확인할 수 있는 프로그램을 공개하였다[15]. 최근 2017년 12월에는 이러한 프로그래밍 환경을 더욱 개선하여 Q# 기반의 Microsoft Quantum Development Kit를 발표하였다[16]. 이는 비주얼 스튜디오와 연동되며, 40개의 큐비트 수준을 지원하는 클라우드 기반 가상 양자머신과도 연동될 수 있다.
3. 향후 연구개발 이슈들
현재 개발되고 있는 양자컴퓨팅의 하드웨어 수준이나 가상 양자머신의 수준은 50-큐비트 정도로 볼 수 있다. 이러한 큐비트 수준에서는 양자컴퓨터가 고전컴퓨터보다 빠르게 계산할 수 있는 쇼어의 알고리즘(2,048 비트)과 같은 대규모의 큐비트와 게이트가 필요한 양자알고리즘은 실행해 보기 어렵다.
이러한 양자알고리즘을 양자컴퓨터에서 효율적으로 실행하기 위해서 양자컴파일 과정에서부터 그 결과물인 양자 어셈블리 코드를 최소로 하여 예상되는 양자컴퓨터 동작시간을 줄여나가는 것이 필요하다. 현재 양자컴퓨터의 컴파일 기술은 QTRL 4 수준의 여러 개의 큐비트가 구현되고, 이들의 고전적인 제어가 가능한 환경에서 사용할 수 있으나, QTRL 6단계의 양자컴퓨팅 기술에서 더욱 중요하게 사용될 것으로 보인다.
양자컴퓨터 프로그래밍 환경은 현재 개발자 중심의 표현으로 되어 있는 부분이 많고, 사용자가 편리하게 사용할 수 있는 라이브러리가 많이 개발되어 있지는 않다. 향후에는 이러한 프로그래밍 환경이 일반 사용자도 쉽게 사용할 수 있도록 더욱 개선되어 나아갈 것으로 생각된다.
Ⅳ. 양자컴퓨터 시스템 합성 및 운영체제 기술 동향
1. 동작원리
양자 노이즈에 취약한 양자 정보를 노이즈로부터 안정적으로 저장, 조작, 전송하기 위해서 양자 오류 정정 기반의 결함허용 양자컴퓨팅 기술이 적용되어야 한다. 결함허용 양자컴퓨팅은 주기적인 양자 오류 정정과 논리적 양자컴퓨팅으로 구성되어 있는데, 논리적 양자컴퓨팅은 양자 정보와 양자 게이트를 양자 오류 정정 부호를 이용해 부호화하여 논리적으로 변환한 뒤 컴퓨팅을 수행하는 것을 말한다. 즉, 결함허용 양자컴퓨팅의 핵심요소는 양자 오류 정정 부호와 해당 부호 맞춤형 오류 복호화 알고리즘 및 논리적 양자 게이트 구현 기술이라 할 수 있다.
Shor가 1990년대 중반 양자 오류 정정 부호[17]와 결함허용 양자 오류 정정 기술[18]을 처음 제안한 후 다양한 종류의 양자 오류 정정 부호와 관련 오류 정정 기술들이 발표되었다. 특히, 양자 노이즈와 노이즈 검출 연산자를 Pauli 그룹의 Commutation/Anti-Commutation 관계로 표현할 수 있는 Stabilizer Formalism[19]-[21]이 제안된 이후 양자 오류 정정 부호 연구는 더욱 활성화를 띄었는데, 다양한 고전 부호 이론의 부호 설계 방법들이 Stabilizer formalism 하에서 양자 부호로 구현되었다. Stabilizer formalism을 우회하는 다른 방식의 양자 오류 정정 부호 체계(Subsystem code, Entanglement-Assisted code)도 많이 연구 개발되었다[22], [23].
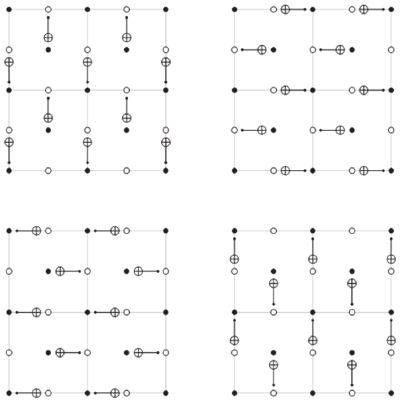
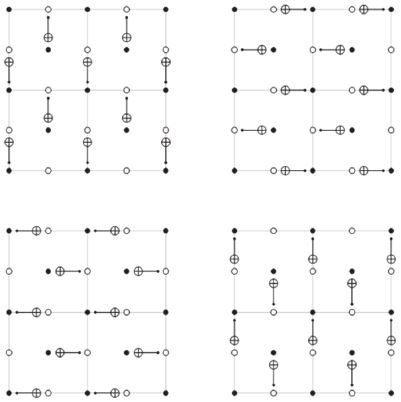
2000년대 중후반부터 위상학적 개체 상에서의 국소성을 기반으로 하는 위상학적 부호(Topological code) 가 주목받고 있다[24]. 부호 자체가 국소성을 기반으로 설계되었기 때문에, 국소적 2-큐비트 게이트 적용이 자연스럽다. 가장 간략한 형태의 위상학적 부호는(2D) surface code인데, 2차원 planar 개체 상에 데이터 큐비트와 보조 큐비트(또는 신드롬 큐비트)를 서로 인접하여 배치하고, 해당 큐비트 간의 2-큐비트 연산을 통해서 오류 측정 및 게이트 연산을 수행하게 된다[(그림 2) 참조]. Surface code의 경우 이런 국소성과 데이터 큐비트만큼 많은 신드롬 큐비트를 사용하는 덕분에 Block 타입 오류 정정 부호보다 매우 높은 부호 임계값(10-2~10-3)을 갖는다[25]. 즉, 물리적 오류율이 10-3 이하이면 surface code 기반 양자 오류 정정이 가능한데, 현재까지 보고된 물리적 게이트의 오류율이 그 정도를 충분히 만족시키기 때문에 Surface code 기반 양자컴퓨팅은 어느 결함허용 양자컴퓨팅 모델보다 실현 가능성이 높다 할 수 있다.
범용 양자컴퓨팅을 구현하기 위해서 1-큐비트 회전 게이트(Rx, Ry, Rz)와 2-큐비트 CNOT 게이트가 필요하다[7]. 양자컴퓨팅 시스템 합성 측면에서 2-큐비트 게이트가 특별한데, 현재까지 구현 가능한 2-큐비트 게이트는 국소적으로 동작하기 때문이다. 게이트의 동작이 국소적이란 대상이 되는 두 개의 큐비트가 서로 인접해서 위치해야 한다는 것을 의미한다. 만약 큐비트들이 서로 떨어져 있다면, 2-큐비트 게이트가 인가되기에 앞서 먼저 큐비트들의 이동이 필요하다. 이런 큐비트의 이동은 양자알고리즘 상에는 명시적으로 드러나지 않지만, 알고리즘 구동을 위해서 반드시 요구되는 오버헤드라 할 수 있다.
큐비트의 이동을 위해서 지금까지 두 가지 방법이 논의되어 왔다[26]. 첫 번째는 인접한 두 개의 큐비트들 사이의 양자 상태를 교환하는 SWAP 게이트 기반 큐비트 이동이다. SWAP 게이트 역시 국소적으로 동작하므로, 두 큐비트 사이 거리만큼 반복적인 SWAP 게이트를 통해서 큐비트가 이동해 간다. 두 번째는 양자 전송 (Quantum Teleportation)을 이용하여 원거리에 위치한 두 개의 큐비트 간 양자 상태를 이동하는 것이다. 양자 전송을 수행하기 위해서 원거리에 위치한 두 큐비트 사이에 얽힌 상태가 먼저 만들어져야 한다. 일반적으로 한 장소에서 얽힌 큐비트 쌍을 만들어 각각의 위치로 전달하는데, 이 과정에서 SWAP 기반 큐비트 이동이 필요할 수 있다.
2. 기술개발 동향
양자컴퓨팅 시스템 매핑은 추상적 양자알고리즘을 구동하고자 하는 물리적 양자컴퓨터에 맞게 재구성하는 과정을 말한다. 양자알고리즘은 어떤 문제를 푸는 과정에 대한 수학적, 추상적 표기인데, 실제 양자컴퓨터가 동작하기 위해서는 물리적 제어 신호가 필요하다. 또한, 양자컴퓨터는 물리적, 논리적 구조로 되어 있는데 일반적으로 양자알고리즘은 양자컴퓨터 구조를 반영하고 있지 않다. 따라서 양자알고리즘을 양자컴퓨터의 특정 구조에 맞게 재구성할 필요가 있다. 이 과정을 시스템 매핑이라 부른다. 시스템 매핑을 위한 양자알고리즘은 앞서 살펴본 양자 어셈블리 코드의 형태를 가지고 있다.
시스템 매핑의 기본 원리는 알고리즘에서 기술된 연산들이 실제 양자컴퓨터상에서 구현될 수 있도록 하는 것이다. 먼저, 특정한 구조상에 큐비트를 배치하고, 양자 어셈블리 코드상의 명령어(양자 게이트와 대상 큐비트)를 하나씩 해석하여 해당 큐비트에 해당 양자 게이트를 인가하도록 한다. 이때, 국소적 게이트 특성이 정확히 반영되어야 한다. 양자알고리즘 상에서는 임의의 2-큐비트를 대상으로 한 CNOT 기술되어 있으므로, 시스템 매핑 과정에서는 해당 CNOT 연산이 정확하게 이루어질 수 있도록 사전에 큐비트의 이동이 이루어지도록 해야 한다. 이때, 큐비트의 이동에 관한 비용(이동량)은 큐비트들의 배치 구조와 초기 배치 형태와 관련이 있다. 그동안 큐비트의 초기 배치를 알고리즘에 맞게 최적화하기 위한 연구결과들이 발표되었는데, 대부분 1D 구조, 소규모 양자알고리즘을 대상으로 휴리스틱하게 접근하였다[27], [28]. 현재 3D 구조상에 큐비트를 배치 및 제어하는 것이 어렵기 때문에, 가장 실현 가능성이 높은 구조는 2D 구조이다.
안정적인 양자알고리즘의 구동에 필요한 게이트의 정확도 요구 수준이 매우 높아서 현재까지 개발된 그리고 당분간의 양자컴퓨팅 하드웨어가 이를 충족시키기 어려울 것으로 보인다. 따라서 양자 오류 정정 기반의 결함허용 양자컴퓨팅 기술이 적용되어야 한다. 앞서 언급했듯이, 기본이 되는 양자 오류 정정 부호에 따라서 논리적 양자 게이트의 구체적인 구현 방법이 다르다. 이후로는 Steane 부호(Block 타입 부호)[20] 와 Surface 부호(Topological 부호)[24]를 기준으로 시스템 합성에서 유의사항에 대해서 살펴본다.
Steane 부호 기반 양자 오류 정정과 논리적 게이트 구현 과정이 임의 거리 간의 상호작용을 전제로 개발되어 있어서, 임의 거리에 위치한 큐비트 간의 CNOT 연산이 많이 포함되어 있다. 따라서 Steane 부호 기반 컴퓨팅을 실제로 실현하기 위해서는 해당 CNOT 연산들을 국소적 CNOT 연산으로 대체해주어야 하는데, 이 과정이 시스템 매핑 과정에서 중요하게 고려되어야 한다. Steane 부호가 개발되고 초창기엔 오류 정정 능력과 임계값 분석 관련 대다수의 연구 역시 임의 거리 간의 상호작용을 전제로 진행되었다. 하지만 2010년 이후로는 국소성 기반의 연구 결과들이 발표되고 있다[29], [30]
Surface 부호의 경우는 부호의 개발 배경이 국소성에 있다. 따라서 Surface code 기반 양자 오류정정과 논리적 게이트의 모든 CNOT 연산이 국소적으로 구성되어 있다. 이런 점에서 Surface code가 단순히 Steane 부호보다 임계값이 높다는 점 외에도 시스템 구현이 용이하다는 장점이 있다. 따라서 Surface code의 시스템 매핑은 Steane 부호보다 수월하다.
양자컴퓨터의 운영체제를 논하기에 앞서, 과연 양자컴퓨터는 어떤 형태를 가질 것인가에 대해서 살펴볼 필요가 있다. 아주 먼 미래의 양자컴퓨터를 상상하긴 어렵고, 근시일 안의 양자컴퓨터의 모습은 지금의 GPU 가속기와 유사할 것이다. Co-processor로써 양자컴퓨팅 하드웨어가 디지털 컴퓨터에 결합되어, 디지털 컴퓨터가 양자컴퓨팅 하드웨어를 제어 관리하는 형태가 현재로서는 유력한 모델이다. 실제로 양자컴퓨팅 하드웨어를 구동하기 위해서 디지털 컴퓨터에 요구되는 역할이 양자 오류 정정부터 양자 게이트 제어 관리까지 매우 중요하다.
위와 같은 양자컴퓨터의 모습을 생각한다면, 양자컴퓨터의 운영체제는 GPU 가속기 제어와 유사한 역할을 해야 한다. 디지털 컴퓨터의 명령으로 양자컴퓨팅 하드웨어 상에 큐비트 공간을 할당 및 초기화하고, 일련의 양자 게이트 명령을 인가하고, 최종적으로는 측정을 통해서 결과를 디지털 컴퓨터에 알려주는 기능을 수행해야 한다. 하지만 기존의 GPU 가속기 제어와 큰 차이가 바로 양자 오류 정정이다. 앞서 언급했듯이, 알고리즘상에는 명시적으로 드러나지 않는 오류 정정을 주기적으로 수행해야 한다. 이 과정은 양자컴퓨터의 운영체제가 양자 게이트와 게이트 사이에 주기적으로 수행해야 한다. 일반적인 양자 오류 정정 과정은 ‘신드롬 측정-오류 확인-회복 연산 적용’으로 구성되는데, 운영체제가 이 과정을 알고리즘 구동 중간에 주기적으로 수행해야 한다[31].
지금까지 대부분의 양자컴퓨팅 제어는 소규모 수준의 알고리즘을 소규모 물리 큐비트 상에 직접 인가하는 것이었다. 연구실 수준에서 수 큐비트의 시스템상에서 비교적 짧은 길이의 알고리즘을 구동하는 것이기에 모든 과정을 수작업으로 할 수 있었다. 따라서 실제 양자컴퓨팅 관련 실험 연구자들에게는 양자컴퓨터를 위한 운영체제라는 용어는 매우 낯설 것이다. 소규모 실험을 제어할 수 있는 제어소프트웨어면 충분하고, 또한 오류 정정을 적용하지도 않는다.
양자컴퓨터 운영체제라는 이름의 연구결과는 최근에야 발표되기 시작했는데, Stanford 대학 연구팀은 대규모 양자컴퓨터를 제어하는 데 필요한 시스템 수준의 요구 조건을 분석하였다[32]. 대규모 양자컴퓨터를 구현하기 위한 설계도[33], [34] 가 제안이 되면서 그런 양자컴퓨터를 실제로 구동하기 위한 제어기술도 연구되기 시작했다. 특히, 오류 정정이 적용된 제어기술이 개발되기 시작했는데, 지난 2017년 9월에 네덜란드 Delft 공대와 인텔 공동 연구팀이 초전도체 큐비트로 구성된 양자컴퓨터 상에서 임의 크기의 Surface code 양자 오류 정정 기술을 제안하였다[35]. 해당 오류 정정은 알고리즘의 구동과 별개로 파이프라인으로 오류 측정을 수행한다.
시스템 매핑은 알고리즘을 구동하기 위해 모든 게이트 시퀀스를 사전에 준비하는 것이다. 그리고 실제 구동 시에는 시퀀스 상의 게이트를 순차적으로 인가하면 된다. 양자 오류 정정 과정을 적용하지 않은 소규모의 양자컴퓨팅 실험을 수행한다면 시스템 매핑 과정에서 정해진 순서대로 게이트들을 인가하면 될 것이다. 모든 것이 사전에 정해져서, 실제 동적으로 결정해야 할 요소들은 없을 것이다. 반면, 결함허용 양자컴퓨팅에서는 다르다. 양자 오류 정정뿐만 아니라 논리적 게이트 프로토콜에도 양자 측정이 포함되어 있고, 측정 결과에 따라서 다음에 인가할 게이트를 선택해야 한다. 즉, 동적으로 결정되는 요소들이 매우 많다. 이는 양자컴퓨터의 운영체제가 담당해야 할 매우 중요한 요소이다. 오스트리아 소재 요하네스 케플러 대학과 구글 공동 연구팀은 지난 2017년 11월 surface code 양자컴퓨팅을 동적으로 스케줄링 하는 기술을 개발해 발표하였는데[36] 양자컴퓨터의 운영체제에 대한 연구가 점점 더 확대되어 가고 있다.
QTRL 관점에서 시스템 매핑은 7단계 수준에 이라고 평가할 수 있다. 시스템 매핑은 물리적 양자컴퓨팅을 수행하기 위한 사전 준비단계로 디지털 프로세싱 작업을 거친다. 이 과정에서 다양한 최적화 기법도 적용 가능하다. 시스템 매핑에 필요한 양자컴퓨터 구조, 양자 오류 정정 부호, 게이트 스케줄링 등의 다양한 요소들은 지속해서 연구 개발되어야 하지만, 시스템 매핑 그 자체로는 성숙한 기술이라고 평할 수 있다.
반면 운영체제는 4단계 수준으로 평가할 수 있다. 현재 소규모의 큐비트들을 제어하여 소규모 알고리즘을 테스트하는 수준이고, 오류 보정을 적용한 큐비트 제어는 아직 이론 연구개발단계에 머물러 있다. 또한, 실제로 물리적으로 실험하기 위해서는 큐비트들의 집적이 더 필요하다.
3. 향후 연구개발 이슈들
지금까지 양자컴퓨팅 시스템 매핑과 운영체제에 대한 연구는 전 세계적으로도 극소수 연구팀에서만 진행되어왔다. 특히, 국내에는 관련 연구팀이 전혀 없다. 따라서 아직 많은 연구가 진행되어야 할 것이다.
현재까지 사용된 양자컴퓨팅 시스템 매핑은 소규모 알고리즘을 대상으로 해왔다. 실제로 사용할 수 있는 양자컴퓨팅 하드웨어도 소규모에 불과해서 대규모 알고리즘, 예를 들어 Shor 알고리즘을 실제로 시스템 매핑할 필요가 없었다. 따라서 관련 기술 개발도 충분하지 않다. 시스템 매핑을 위해서 양자 어셈블리어 형태의 양자알고리즘이 이용되는데, 그동안 주로 사용해온 어셈블리어는 단순한 양자 게이트 리스트 형태의 비구조적 어셈블리어이다[12], [37]. 이 어셈블리어는 알고리즘의 크기가 증가함에 따라 그 크기가 거의 지수적으로 증가한다. 따라서 대규모 양자알고리즘의 경우 양자 어셈블리어를 생성 관리하는 것부터 큰 비용이 발생한다. 양자컴퓨팅이 큰 역할을 할 수 있는 문제 영역은 디지털 컴퓨터가 해결하는 데 어려움을 겪고 있는 대규모 문제이기 때문에, 대규모 양자알고리즘에 대한 시스템 매핑 기술 개발이 필요하다.
양자컴퓨팅 운영체제 관련해서는 구성요소들의 성능 향상 측면에서 연구개발이 계속되어야 한다. 대표적인 것들이 양자 오류정정 오류 복호화 기능과 큐비트 관리 제어 기능이다. 앞서 언급했듯이, 양자 오류 정정은 알고리즘 구동 중에 지속해서 수행되어야 하고, 양자 오류정정 과정은 운영체제가 관리해야 하는 기능이다. 양자 오류정정 과정에 지연이 발생하면 큐비트의 상태가 오염되어 본래의 상태를 잃어버리게 되기 때문에, 빠른 양자 오류 정정 기술은 필수적이다. 또한, 많은 큐비트를 효과적으로 관리해야 한다. Shor 알고리즘 같은 대규모 양자알고리즘을 구동하는 데 필요한 물리 큐비트의 개수는 수억~수십억 개에 이를 것으로 추정된다. 그렇게 많은 수의 큐비트를 효과적으로 잘 관리하고 병렬적으로 제어하는 기능은 매우 필수적이다. 큐비트 수가 많아지면 큐비트 간의 동기화가 큰 문제가 될 수 있을 것이다.
Ⅴ. 양자컴퓨터 프로세서 기술 동향
1. 동작원리
양자컴퓨팅에 사용되는 정보 단위인 큐비트는 양자역학적으로 독립된 2개의 상태로 구성된 시스템이다. 이러한 상태는 단일 광자의 존재 여부, 전자의 스핀 업 상태 혹은 다운 상태 등으로 만들 수 있다. 여러 큐비트를 모아 양자역학적 연산을 수행하여 양자컴퓨팅을 구현할 수 있다. 이러한 양자 역학적 상태를 유지하는 것은 외부 환경과의 차단이 요구되나, 큐비트 간의 연산을 수행할 때에는 외부 환경과의 상호작용이 요구되므로 원하는 시점에서의 상호작용 제어가 용이해야 한다.
큐비트를 양자컴퓨팅에 사용하기 위하여는 다음 네 가지 조건을 만족해야 한다[38]. Divincenzo의 양자컴퓨팅을 위한 조건이 있지만, 여러 새로운 큐비트에 대한 물질과 시스템이 등장함에 따라 여러 새로운 큐비트의 조건에 알맞게 적용할 수 있는 일반화된 조건이다. 네 가지 조건은 충분한 결맞음 시간, 확장성, 범용성, 신뢰성을 갖추는 것이다. 큐비트는 우리가 원할 때 연산을 하며, 그 외의 경우에는 외부와 차단되어 있어야 한다. 양자 상태는 매우 외부 환경에 민감하게 반응하여 원래의 정보를 잃기 쉽기 때문이다. 결맞음 시간이란 양자정보를 유지할 수 있는 시간이다. 따라서, 양자컴퓨팅은 결맞음 시간 동안 연산을 할 수 있으므로, 충분히 긴 결맞음 시간이 필요하다. 두 번째로, 확장성이 보장되어야 한다. 큐비트를 늘려나갈 때 시간, 공간, 에너지 등이 기하급수적으로 증가해서는 안 된다. 구체적으로는 큐비트를 늘리고 조작하는 데 요구되는 비용이 양자 연산을 하여 얻는 이득보다는 적어야 한다. 세 번째는 범용성이 보장되어야 한다. 이는 기술될 수 있는 모든 큐비트 상태를 우리가 한정적인 조작을 통해 바꿀 수 있다는 것이다. 따라서 특정 큐비트 시스템에서는 범용성이 큐비트의 상태의 초기화 및 측정과 단일 큐비트 연산, 그리고 CNOT 게이트 등의 다중 큐비트 연산이 가능함을 의미한다. 마지막 조건은 신뢰성이 보장되어야 한다. 양자 오류 정정은 양자 정보의 신뢰성을 보장할 수 있다. 양자 오류 정정을 통해 양자 연산 도중 오류가 발생하더라도, 오류를 감지하여 원하던 양자 정보를 산출할 수 있다.
2. 기술개발 동향
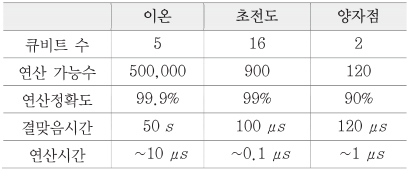
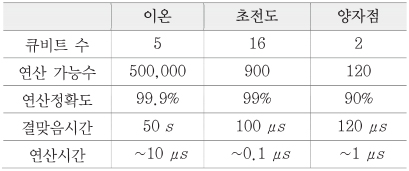
큐비트는 단일 원자나 이온을 가두어 만든 큐비트, 초전도 상태를 이용한 큐비트, 결함을 이용하여 만든 큐비트, 양자점을 이용하여 만든 큐비트, 위상학적 상태를 이용한 큐비트 등 여러 가지 방법으로 구현되어 있다. 양자컴퓨팅에 사용하기 위해서 충분한 수의 큐비트를 구현하여, 양자정보를 필요한 시간 동안 유지하여 높은 정확도로 연산을 수행해야 한다. 아직 물리적 큐비트는 TRL으로는 2~4단계로, 앞서 시스템 합성이나 운영체제에서 기대하는 양자컴퓨팅과는 아직 거리가 있다. 우선 최근의 기술 동향을 앞서 언급한 3가지 요소를 위주로 살펴보겠다.[<표 2> 참조]
먼저 구현된 큐비트 수를 살펴보면, 최근에는 단일 이온들을 이용하여 5개의 큐비트 간 상호 작용이 가능한 시스템이 보고되었다[39]. 또한, 구글[40], IBM[41]에서는 9개, 16개의 큐비트 시스템이 각각 공개되었으며, 50개 큐비트 규모의 프로토타입을 제작[42]하였다. 큐비트 수를 늘리기 위하여 이온 트랩 큐비트, 양자점 큐비트 시스템에서 2차원 배열로 확장 가능한 큐비트 시스템을 제안하여 연구 중이다.
다음으로, 양자 정보를 유지하여 연산 가능 시간을 판단하려면 양자 정보를 얼마나 긴 시간 동안 유지할 수 있는지, 정보 처리를 위한 소요시간이 얼마인지 알아보아야 한다. 큐비트가 양자정보를 유지할 수 있는 시간을 결맞음 시간으로 판단하는데 이온트랩은 50 초[43], 초전도 큐비트는 90 마이크로초[42], 양자점 큐비트는 120 마이크로초[44]까지 보고되었다. 한편, 연산에 소요되는 시간은 구현 시스템마다 상이하나, 이온은 10 마이크로초, 초전도 큐비트는 0.1 마이크로초, 양자점은 1 마이크로초 정도이다. 따라서, 연산 가능 시간은 대략 이온트랩의 경우 50만 회, 초전도 큐비트는 900 회, 이온은 120 회 정도의 연산을 할 수 있다.
큐비트의 연산 정확도 또한 매우 중요한 이슈이다. 현재의 양자 게이트 연산 정확도는 매우 긴 크기의 알고리즘에 수행할 경우, 그 연산 후의 신뢰도가 충분하지 않다. 이온의 경우 다중 큐비트 연산의 경우 99.9%[43], 초전도체의 경우 99%[45], 양자점 큐비트는 90%[46], 다이아몬드 NV 센터 큐비트는 88%[47]로 보고되었다.
3. 향후 연구개발 이슈들
어떠한 큐비트 기술이 적용되더라도 대규모 양자컴퓨팅을 위하여는 많은 수의 큐비트에 대하여 많은 연산이 가능하고, 그 정확도는 매우 높아야 한다. 단기적인 목표로 큐비트 수를 점점 늘려나가 양자컴퓨팅의 규모를 늘리는 것이 현재의 당면 과제이다. 이는 특정 상황에서 양자컴퓨팅의 우월성을 보일 수 있을 뿐만 아니라, 추후 대규모 양자컴퓨팅의 핵심인 양자 오류 정정 부호의 가능성을 보일 발판을 보여줄 수 있다. 특히 큐비트 수가 늘어날수록 조작, 상호 오류, 등 시스템의 복잡도가 매우 빠르게 증가하기 때문에 이를 간소화하는 것 또한 중요해진다. 더 나아가, 대규모 양자컴퓨팅을 위해서는 양자 오류 정정 부호를 활용하여 정확성을 더욱 엄밀하게 할 필요가 있다. 양자 오류 정정 부호를 활용하기 위하여는 반드시 그 바탕이 되는 큐비트의 오류율이 특정 임계값을 만족해야 한다. 또한, 해당 큐비트의 오류율에 따라 양자 오류 정정 부호의 성능 향상 정도가 달라진다. 한편, 큐비트의 수가 늘어나면 큐비트 간 국소적 연결이 달라지기 때문에, 이는 큐비트의 오류를 더 누적시킬 수 있어 오류 정정 부호 구현에 영향을 미치게 된다. 그러므로 큐비트 시스템을 구성하면서 효과적인 배치와 상호작용 또한 고려해야 한다.
Ⅵ. 결론
본고에서는 양자 정보통신분야 중에서 양자컴퓨팅과 관련한 구성요소들의 개념과 관련 연구개발 동향을 살펴보았다. 현재 양자컴퓨팅은 주요 국가에서도 집중적으로 연구개발이 진행되고 있으며, 주요 글로벌 기업에서도 관련한 연구개발을 진행하고 있다. 이러한 근본 원인은 양자컴퓨팅이 차세대 컴퓨팅으로, 기존의 방식과는 전혀 다른 형태의 연산이 가능하기 때문이다.
우리나라도 양자컴퓨팅에 대한 연구개발을 집중해야 한다. 이는 단순히 해외 양자컴퓨팅 연구팀과의 기술적 격차를 감소시키기 위한 것이 아니라, 양자컴퓨팅이 갖는 잠재적 보안위협과 동시에 활용가치가 매우 높기 때문이다. 양자컴퓨팅을 연구·개발하는 상당히 다양한 연구개발 분야가 융합되어야 하므로 부분적 기술만 잘 발달된다고 해서 완성되는 것도 아니다. 이에 따라 양자컴퓨팅과 관련하여 기술적 수준을 높이기 위해서 지금부터는 전체적 접근에서의 연구개발이 이루어져야 할 것으로 기대된다.
용어해설
양자 오류 정정양자 정보 처리 디바이스에 발생한 양자 노이즈의 효과를 억제하는 기술
양자 운영체제양자컴퓨팅 디바이스상에서 양자알고리즘을 구동하는 제어 소프트웨어, 백그라운드로 양자오류정정을 수행하면서 양자알고리즘을 구동하는 체계
가상 양자머신양자컴퓨팅을 시뮬레이션하는 비트기반 컴퓨터
약어 정리
R.P. Feynman, “Simulating Physics with Computers,” Int. J. Theoretical Phys., June 1982, vol. 21, no. 6-7, pp. 467-488.
P.W. Shor, “Algorithms for Quantum Computation: Discrete Logarithms and Factoring,” Proc. Annu. Symp. Found. Comput. Sci., Santa Fe, NM, USA, Nov. 1994, pp. 124-134.
L.K. Grover, “A fast Quantum Mechanical Algorithm for Database Search,” Proc. Annu. ACM Symp. Theory Comput., Philadelphia, PA, USA, May 22-24, 1996, pp. 212-219.
P.J.J. O’Malley et al., “Scalable Quantum Simulation of Molecular Energies,” Phys. Rev. X, vol. 6, July 2016, Article no. 031007.
A. Kandala et al., “Hardware-Efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets,” Nature, vol. 549, 2017, pp. 242-246.
Forschungszentrum Julich, Accessed Jan. 2018. http://www.fz-juelich.de/ias/jsc/EN/Research/ModellingSimulation/QIP/QTRL/_node.html
M. Nielsen and I. Chuang, Quantum Computation and Quantum Information, Cambridge, UK: Cambridge Univ. Press, 2000.
B. Omer, “A procedural formalism for quantum computing,” Master’s thesis, Department of Theoretical Physics, Technical University of Vienna, 1998.
J.W. Sanders and P. Zuliani, “Quantum Programming,” In Mathematics of Program Construction, New York, USA: Springer, 2000, pp. 80-99.
S. Bettelli, T. Calarco, and L. Serafini, “Toward an Architecture for Quantum Programming,” Eur. Phys. J. D-Atomic, Molecular, Opt. Plasma Phys., vol. 25, no. 2, 2003, pp. 181-200.
A.S. Green et al., “Quipper: a Scalable Quantum Programming Language,” Proc. ACM SIGPLAN Conf. Programming Language Des. Implementation, Seattle, WA, USA, June 2013, pp. 333-342.
A. JavadiAbhari et al., “ScaffCC: a Framework for Compilation and Analysis of Quantum Computing Programs,” Proc. ACM Conf. Comput. Frontiers, Cagliari, Italy, May 2014, Article no. 1.
Google Research Blog, Accessed Jan. 2018. https://research.googleblog.com/2017/10/announcing-openfermion-open-source.html
Microsoft, Accessed Jan. 2018. https://www.microsoft.com/en-us/research/project/language-integrated-quantum-operations-liqui
Microsoft Quantum, Accessed Jan. 2018. https://cloudblogs.microsoft.com/quantum/2017/12/11/announcing-microsoft-quantum-development-kit/
P. Shor, “Scheme for Reducing Decoherence in Quantum Computer Memory,” Phys. Rev. A, vol. 52, Oct. 1995, Article no. R2493.
P. Shor, “Fault-Tolerant Quantum Computation,” Symp. Found. Comput., Burlington, VT, USA, 1996.
A.R. Calderbank and P. Shor, “Good Quantum Error-Correcting Codes Exist,” Phys. Rev. A, vol. 54, no. 2, 1996, pp. 1098-1105.
A. Steane, “Multiple-Particle Interference and Quantum Error Correction,” Proc. Royal Soc. A, vol. 452, no. 1954, Nov. 1996, pp. 2551-2577.
D. Gottesman, “Class of Quantum Error-Correcting Codes Saturating the Quantum Hamming Bound,” Phys. Rev. A, vol. 54, no. 3, Sept. 1996, pp. 1862-1868.
D. Bacon, “Operator quantum Error-Correcting Subsystems for Self-Correcting Quantum Memories,” Phys. Rev. A, vol. 73, 1996, Article no. 012340.
M.-H. Hsieh et al., “General entanglement-Assisted Quantum Error-Correcting Codes,” Phys. Rev. A, vol. 76, 2007, Article no. 062313.
A.Y. Kitaev, “Fault-Tolerant Quantum Computation by Anyons,” Ann. Phys., vol. 303, no. 1, Jan. 2004, pp. 2-30.
D.S. Wang et al., “Surface Code Quantum Computing with Error Rates Over 1%,” Phys. Rev. A, vol. 83, Feb. 2001, Article no. 020302(R).
M. Oskin et al., “Building Quantum Wires: The Long and the Short of It,” Annu. ISCA, San Diego, CA, USA, June 2003, 374-385.
M. Pedram and A. Shafaei, “Layout Optimization for Quantum Circuits with Linear Nearest Neighbor Architectures,” IEEE Circuits Syst. Mag., vol. 16, no. 22016, pp. 62-74.
A. Shafaei et al., “Optimization of Quantum Circuits for Interaction Distance in Linear Nearest Neighbor Architectures,” Des. Automation Conf., Austin, TX, USA, 2013, pp. 1-6.
K.M. Svore et al., “Local Fault-Tolerant Quantum Computation,” Phys. Rev. A, vol. 72, Aug. 2005, Article no. 022317.
K.M. Svore et al., “Noise Threshold for a Fault-Tolerant Two-Dimensional Lattice Architecture,” Quantum Inform. Comput., vol. 7, no. 4, May 2007, pp. 297-318.
H. Corrigan-Gibbs, D.J. Wu, and D. Boneh, “Quantum Operating Systems,” Proc. HotOS, Whistler, Canada, May 2017, pp. 76-81.
B. Lekitsch et al., “Blueprint for a Microwave Trapped Ion Quantum Computer,” Sci. Adv., vol. 3, no. 2, Feb. 2017, Article no. e1601540.
A. Paler et al., Online Scheduled Execution of Quantum Circuits Protected by Surface Codes, Nov. 2017, Accessed Jan. 2018. https://arxiv.org/abs/1711.01385
R. Versluis et al., “Scalable Quantum Circuit and Control for a Superconducting Surface Code,” Phys. Rev. Appl., vol. 8, Sept. 2017, Article no. 034021.
R. Van Meter and C. Horsman, “A Blueprint for Building a Quantum Computer,” Commun. ACM, vol. 56, no. 10, 2017, pp. 84-93.
S. Debnath et al., “Demonstration of a Small Programmable Quantum Computer with Atomic Qubits,” Nature, vol. 536, Aug. 2016, pp. 63-66.
J. Kelly et al., “State Preservation by Repetitive Error Detection in a Superconducting Quantum Circuit,” Nature, vol. 519, Mar. 2015, pp. 66-69.
C. Vu, IBM Announces Advances to IBM Quantum Systems & Ecosystem, Accessed Jan. 2018. http://www-03.ibm.com/press/us/en/pressrelease/53374.wss
T.P. Harty et al., “High-Fidelity Preparation, Gates, Memory, and Readout of a Trapped-Ion Quantum Bit,” Phys. Rev. Lett., vol. 113, Nov. 2014, Article no. 220501.
M. Veldhorst et al., “A two-qubit logic gate in silicon,” Nature, vol. 526, Oct. 2015, pp. 410-414.
R. Barends et al., “Superconducting Quantum Circuits at the Surface Code Threshold for Fault Tolerance,” Nature, vol. 508, Apr. 2014, pp. 500-503.
J.M. Nichol et al., “High-Fidelity Entangling Gate for Double-Quantum-Dot Spin Qubits,” npj Quantum Inform., vol. 3, Jan. 2017, Article no. 3.
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.