무선 통신 물리 계층의 기계학습 활용 동향
Research Trends on Physical Layers in Wireless Communications Using Machine Learning
- 저자
-
최윤호씨앗기술연구실 wing0123@etri.re.kr 강현덕씨앗기술연구실 henry@etri.re.kr 김도영씨앗기술연구실 dyk@etri.re.kr 이재호씨앗기술연구실 jaeholee@etri.re.kr 박윤옥씨앗기술연구실 parkyo@etri.re.kr
- 권호
- 33권 2호 (통권 170)
- 논문구분
- 일반논문
- 페이지
- 39-47
- 발행일자
- 2018.04.01
- DOI
- 10.22648/ETRI.2018.J.330205
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- The fundamental problem of communica-tion is that of transmitting a message from a source to a destination over a channel through the use of a transmitter and receiver. To derive a theoretically optimal solution, the transmitter and receiver can be divided into several processing blocks, with each component analyzed and optimized. The idea of machine learning (or deep learning) communications systems goes back to the original definition of the communi-cation problem, and optimizes the transmitter and receiver jointly. Alt-hough today’s systems have been opti-mized over the last decades, and it seems difficult to compete with their performance, deep learning based commu-nication is attractive owing to its simplicity and the fact that it can learn to communicate over any type of channel without the need for mathemati-cal modeling or analysis.
Share
Ⅰ. 머리말
무선 통신 기술은 무선 네트워크에서 서비스와 응용 프로그램을 만족시키기 위해 광범위한 발전을 해왔다. 최근 지능형 무선 터미널 액세스, 가상 현실, 증강 현실 및 IoT와 같은 분야에서 무선 통신의 응용은 수천 배의 용량, 밀리 초 단위의 저지연 및 대규모 연결성의 방향으로 발전되고 있다. 이에 대한 대안으로 Massive MIMO(Multi-Input Multi-Output), 밀리미터파 및 UDN(Ultra-Densification Network) 등의 무선 데이터 처리 기술이 제안 및 사용되고 있다.
그러나 기존의 통신 이론에 기반한 무선 통신은 대용량 데이터 처리 및 초고속 통신에서 몇 가지 다음과 같은 제한 사항이 있다[1].
1) 어려운 채널 모델링: 통신 시스템의 설계는 실제 채널 조건에 의존적이며, 수학적으로 실제 환경의 특성을 모델링한다. 이러한 모델들은 불완전성과 비선형성을 갖는 환경에 적용하기 어렵다. 예를 들면, Massive MIMO 시스템에서 증가된 안테나 수는 변화된 채널 특성을 가지며, 해당 채널 특성은 아직 알려지지 않았다.
2) 효과적이고 빠른 신호 처리에 대한 요구: 수신 처리 알고리즘은 채널 추정 및 검출을 위해 저해상도 ADC(Analog-Digital Converter)와 같은 저전력 저가격 하드웨어를 사용한다. 그러나 이 알고리즘은 계산의 복잡성을 증가시킬 수 있으며, MIMO 데이터 탐지 알고리즘과 같은 전통적인 알고리즘은 실시간 병목 현상이 발생하기 때문에, 진보된 시스템(Massive MIMO, mmWave, UDN)을 위한 실시간 대용량 데이터 처리 능력이 필요하다. 따라서 알고리즘 구조의 효율성과 정확성을 달성하기 위해 병렬 신호 처리가 필요하다.
3) 제한된 블록 구조 통신 시스템: 코딩, 변조, 감지 및 탐지처럼 일련의 신호 처리 블록들로 구성된 기존의 통신 시스템은 각 블록의 최적화를 통하여 불완전한 채널의 문제를 해결한다. 통신의 근본적인 문제는 메시지가 송신기에 의해 송신되고, 채널을 가로질러 수신되고. 수신 측에서 신뢰성 있는 메시지를 복구하는 것이기 때문에, 연구자들은 각각의 프로세스 알고리즘을 최적화하였고, 실제로 많은 성과를 이루었다. 기계 학습에 의한 새로운 방법은 비록 현재의 시스템이 지난 수십 년간 최적화 되어왔고 성능 면에서 경쟁하기 어렵겠지만, 이전의 방식인 수학적 모델링 및 분석의 필요성 없이 모든 유형의 채널을 통해 최적으로 통신하는 법을 배울 수 있다는 측면에서 충분히 매력적이다[2].
컴퓨터 비전, 자동 음성인식(ASR: Automatic Speech Recognition) 및 자연어 처리(NLP: Natural Language Processing)에서의 딥러닝(DL: Deep Learning)의 성공적인 적용으로 최근 기계학습(ML: Machine Learning)이 주목받고 있다. 그리고 연구자들은 무선 통신을 포함한 다른 영역에도 이러한 기술의 확장 적용을 시도하고 있다. 통신 시스템의 광범위한 영역에서 기계학습 이론은 무선 전송 접속 기술, 이종망(Heterogeneous) 접속 기술, 네트워크, 보안 기술 및 CR(Cognitive Radio), 자원 관리, 링크 적응(Link Adaptation) 등 상위 계층에서 몇 가지 성공을 거두었다[3].
연구자들은 변조 인식(Modulation Recognition), 채널 모델링 및 식별(Identification), 부호화 및 복호화, 채널 추정 및 Equalization과 같은 물리 계층(Physical Layer)에 기계학습 적용을 시도하였다. 그러나 물리 채널의 복잡성과 기존 기계학습 알고리즘의 제한된 학습 능력 때문에 기계학습은 상업적으로 사용되지 못하였지만, 물리 계층에 딥러닝을 도입함으로써 기계학습의 성능이 향후 크게 향상될 것이다.
딥러닝은 기존의 기계학습 알고리즘에 비해 상당한 구조의 유연성 향상을 보이기 때문에, 딥러닝 기반의 통신 시스템은 다음과 같은 가능성을 가진다[4].
첫째, 통신에서 대부분의 신호 처리 알고리즘은 통계 및 정보 이론에 수학적으로 모듈화가 가능하고, 선형적이며 Gaussian 통계에 견고한 토대를 가진다. 그러나 실제적인 시스템은 많은 비선형성을 가진다. 이러한 이유로, 수학적 모델이 필요하지 않고 특정 하드웨어 구성 및 채널을 위한 최적화가 가능한 딥러닝 기반의 통신 시스템은 이러한 불완전성을 보다 잘 최적화할 수 있다.
둘째, 통신 시스템 설계의 기본적인 원리 중 하나는 각각의 잘 정의되고 독립된 기능을 갖는 다수의 블록체인으로 신호 처리를 분할하는 것이다. 이 접근 방식은 효율적이고 다양한 제어가 가능하지만, 개별적으로 최적화된 프로세싱 블록들이 최상의 end-to-end 성능을 보장하는 것은 아니다. 예를 들면, 많은 실제 채널에서 소스 코딩과 채널 코딩의 분리는 차선책으로 알려져 있다. 각각의 구성 요소를 함께 최적화하는 시도는 다루기 어렵고 계산적으로 복잡한 시스템에서는 이득을 제공한다. 반면, 학습된 end-to-end 통신 시스템은 성능의 최적화가 가능할 것이다.
셋째, 최근 연구에서 NN(Neural Network)은 보편적으로 적용 가능한 것으로 밝혀졌으며, RNN(Recurrent NN)이 주목할만한 알고리즘 학습 방법으로 보여진다. NN의 실행이 병렬화가 가능하고 저 정밀도의 데이터 유형에서 쉽게 구현 가능하기 때문에, 이 형태를 취하는 학습된 알고리즘은 다른 방법보다 빠르면서도 에너지 비용이 적게 든다. 게다가 tensorflow, theano, caffe, MXNet과 같은 다양한 라이브러리와 프레임워크에 의해 딥러닝 기술의 다양한 적용을 가속화 한다.
넷째, GPU와 같은 분산 메모리 구조를 사용한 대규모의 병렬 처리 구조는 매우 효율적이며 놀라운 계산 처리가 가능하다. 그러나 이와 같은 구조의 성능은 효율적인 사용을 위한 높은 수준의 프로그래밍 언어와 알고리즘 능력에 의해 제한된다. 넓고 깊은 딥러닝은 최소한의 튜닝과 최적화를 통해 높은 리소스 활용률을 보인다.
무선 통신 시스템을 위한 딥러닝의 최근 연구는 기존의 통신 시스템의 특정 부분을 향상시키기 위한 대체 접근법과 autoencoder에 기반을 둔 새로운 구조를 통한 전체 시스템의 대체를 제안하고 있다.
본고는 물리 계층에 집중하여 최근 연구를 소개하고자 한다. 또한, 딥러닝 기반의 통신 시스템에 대한 잠재력과 향후 연구를 위한 지침, 동기 부여를 강조하는 것을 목표로 한다. Ⅱ장에서 딥러닝의 기본 개념에 대한 간략한 개요를 제공하고, Ⅲ장에서는 통신 시스템의 대안으로서 딥러닝을 사용한 몇 가지 사례를 제시한다. Ⅳ장에서는 autoencoder에 기반을 둔 새로운 통신 구조를 소개하고, V장에서 맺음말로 마무리한다.
Ⅱ. 딥러닝의 기본 개념
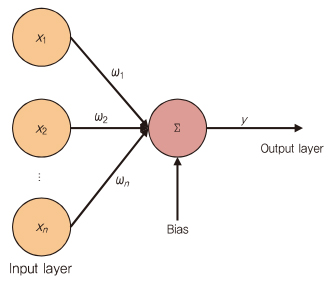
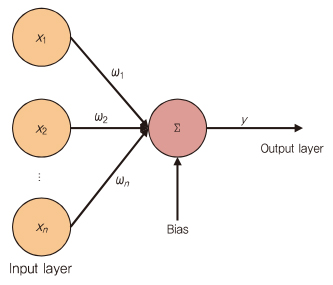
20세기부터의 오랜 연구 끝에, 로지스틱 회귀(Logistic regression), 의사 결정 트리, SVM(Support Vector Machine) 및 신경망 네트워크(NN)와 같은 다양한 알고리즘이 제안되었다. NN이 주목되는 알고리즘인 것처럼, 딥러닝은 (그림 1)과 같이 생물학적 신경 시스템을 시뮬레이션한 신경망 모델링으로부터 유도된다.
바이어스가 있는 여러 입력의 가중치 합계가 활성화 함수(보통 sigmoid 함수)를 거쳐 출력된다.
가장 단순한 NN은 하나의 입력 레이어와 출력 레이어로 구성된 퍼셉트론(perceptron)이라 불린다. 보통 손실 함수(square error, cross entropy)는 실제 값과 예측값이 가능한 한 가까워지도록 구성된다. GD(Gradient descent)는 이러한 손실 함수의 값이 최소화되도록 가중치와 바이어스의 매개 변수를 학습하는 데 사용된다. 선형적으로 분리된 문제를 해결하면, 단일 퍼셉트론은 비선형 특성에 도입되고, 입력 레이어와 출력 레이어 사이의 추가적인 숨겨진 레이어(Hidden layer)와 뉴런을 통하여 보편적인 기능을 갖는 함수로 사용된다.
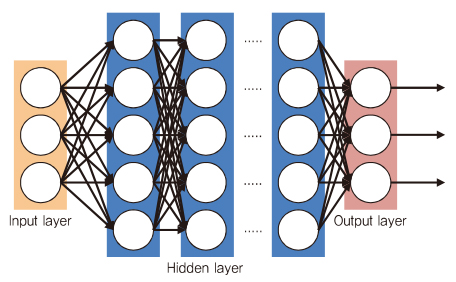
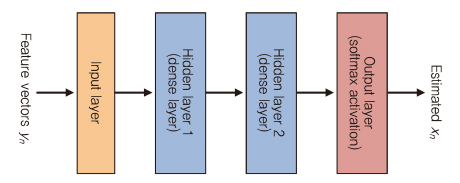
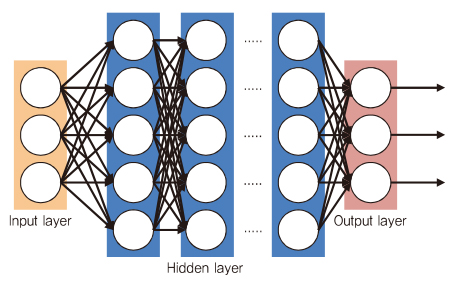
기본적인 딥러닝 모델은 (그림 2)와 같이 각 뉴런은 인접한 레이어에 연결되고, 동일한 레이어에는 연결되지 않는다.
역전파(Back propagation) 알고리즘은 최적화를 위해 GD를 사용한 네트워크처럼 효율적인 학습 방법으로 제안되었다. 그러나 증가되어 숨겨진 레이어와 뉴런 수는 다른 매개 변수를 발생시키고, 그로 인하여 vanishing gradients, 느린 수렴 속도 등과 같은 많은 문제를 발생시켜 네트워크 구성을 어렵게 만든다.
Vanishing gradient의 문제를 해결하기 위해 전통적인 sigmoid 함수 대신 ReLU(Rectified Linear Units)라는 함수가 도입되었다. 더 빠른 수렴 속도와 계산의 복잡도를 줄이기 위한 방법으로, 매회 손실과 기울기를 계산하기 위해 무작위로 하나의 표본을 선택하는 SGD(Stochastic GD)가 제안되었다. 로컬 최적 솔루션 문제를 해결하고 학습 속도를 높이기 위해서는 Adagrad, RMSprop, Momentum, Adam과 같은 적응 학습 알고리즘이 제안되었다. 비록, 학습된 네트워크가 학습 데이터에서는 잘 동작하지만, overfitting에 의해 테스트 데이터에서 성능이 떨어질 수 있다. 이 경우 조기 정지, 정규화 및 dropout이 학습 데이터와 테스트 데이터에서 좋은 결과를 낼 수 있도록 제안되었다.
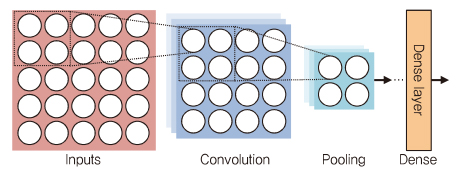
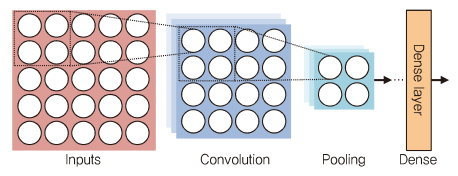
CNN(Convolution NN)은 완전히 연결된 피드 포워드(Feedforward) 네트워크로부터 매개 변수의 급속한 증가를 방지하는 DNN 구조로, 주로 이미지 인식 분야에서 사용된다. CNN의 기본 개념은 (그림 3)과 같이 완전히 연결된 네트워크에 Convolution 레이어와 풀링(Pooling) 레이어를 추가하는 것이다.
Convolution 레이어에서 각 뉴런은 오직 이전 인접한 레이어의 일부 뉴런에만 연결된다. 매트릭스 형태로 구성된 이 뉴런들은 몇몇의 특징 맵을 형성하고, 각 맵에서 동일한 가중치를 공유한다. Pooling 레이어에서 특징 맵의 뉴런들은 평균값(Average pooling)이나 최댓값(Max pooling)을 계산하기 위해 그룹화되며, 이로 인해 매개 변수를 줄일 수 있다.
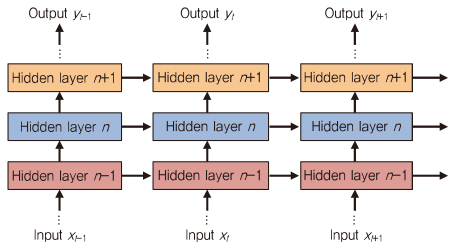
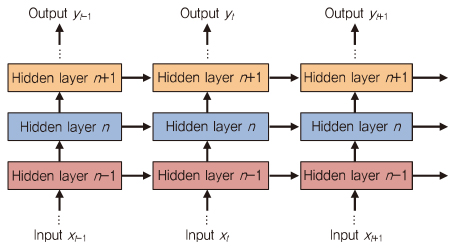
RNN(Recurrent NN)의 목적은 기억(Memory)을 갖는 NN을 제공하는 것이다. 이는 (그림 4)와 같이 출력이 현재의 입력 정보뿐만 아니라, 이전의 정보에도 영향을 받는 것을 의미한다.
Ⅲ. 통신 시스템의 대안으로서의 딥러닝
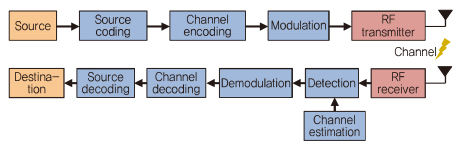
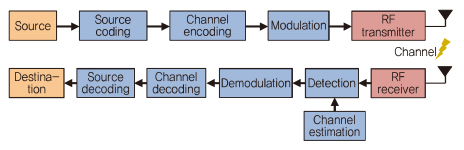
일반적인 무선 통신 시스템의 구조는 (그림 5)와 같으며, 전문적인 지식에 기반한 다양한 알고리즘이 긴 시간 동안 각 처리 블록을 최적하는 방향에서 발전해왔다.
이 섹션에서는 딥러닝이 개별 작업을 대체하는 알고리즘으로 적용된 몇 가지 예를 다룬다.
1. Modulation Recognition
Modulation recognition은 서로 다른 통신 시스템 사이에서 통신을 용이하게 하기 위해 수신된 잡음 신호의 변조 방식을 구별하는 것을 목적으로 한다. 변조 인식에 관한 연구는 기존 알고리즘(의사 결정 이론과 패턴 인식 접근)을 사용하여 수년간 연구되어 왔다.
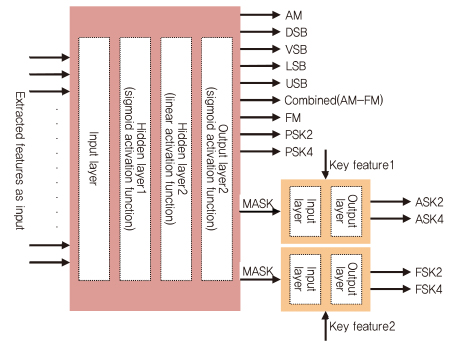
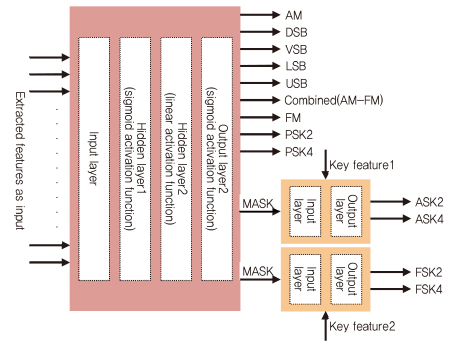
(그림 6)과 같이, 아날로그 변조 방식(AM, DSB, FM)과 디지털 변조 방식(MPSK, MASK, MFSK)의 13가지의 잡음이 섞인 대역 제한 변조 신호에서 식별하는 변조 분류기가 제안되었다. 이 접근 방식은 원래의 신호 및 진폭, 위상, 주파수의 아날로그 또는 디지털 변조 특징을 식별할 수 있다[5].
2. Channel Decoding
기계학습에 기반한 채널 디코더는 1990년대에 등장하였으며 다음과 같은 특징을 보인다[1].
첫째, 채널 디코딩 알고리즘은 비트 레벨 처리가 가능하기 때문에, 비트 또는 LLR(Log-Likelihood Rations)을 입력과 NN이 예측한 출력으로 처리할 수 있다. 입력과 출력 노드는 비트들로 직접 나타내거나, 오직 하나의 1과 나머지는 0으로 표현되는 one-hot으로 표현된다.
둘째, dataset을 얻기 어려울 때와 달리, 사람이 만든 코드가 충분한 학습 샘플을 만들고 labeled 출력을 얻을 수 있다. 게다가 NN은 코드의 잡음 버전으로부터 학습할 수 있고, 코드가 각 학습 epoch에서 채널 잡음에 의해 다른 샘플로 무작위화 되기 때문에 오버피팅 문제를 피할 수 있다.
정보 이론에 기초하여 설계되고 종종 반복 처리 시간이 길어지는 기존의 디코더와 비교할 때, NN 구조는 전문적인 지식이 필요하지 않다. 디코더의 학습 후에 디코딩 과정은 낮은 지연을 갖는다. 게다가 기존의 잘 발달된 디코딩 알고리즘은 새롭게 제시되는 딥러닝 기반 방법의 성능과 비교하는 대상이 될 수 있다.
이러한 장점에도 불구하고, NN 기반의 디코더는 기본적으로 학습의 복잡성이 블록 길이와 함께 증가하기 때문에 확장성이 제한된다. 다행히 딥러닝 알고리즘은 복잡한 계산을 위한 병렬 처리가 가능하기 때문에, 실현 가능한 학습 방법을 갖춘 다중 계층 구조를 제공할 수 있다.
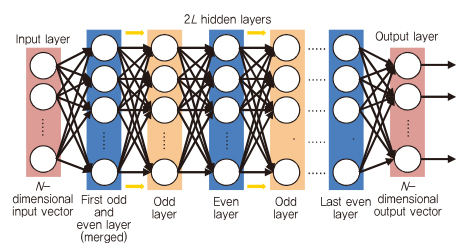
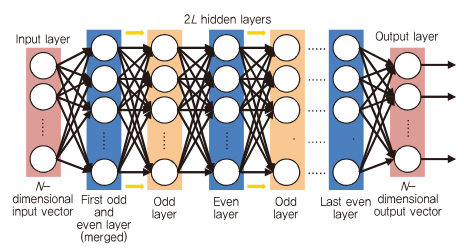
(그림 7)과 같이 완전히 연결된 DNN(Deep Neural Network) 기반의 디코더는 HDPC(High-Density Parity Check) 코드에서 BP(Belief Propagation) 알고리즘의 성능을 향상시키기 위해 제안되었다[6]. BP 알고리즘은 low-density 패리티 체크 코드에서는 shannon 용량에 거의 도달할 수 있지만, 오늘날 흔히 사용되는 HDPC 코드를 디코딩하는 데는 어려움이 있다. 기존의 BP 디코더는 각 변수 노드가 일부 체크 노드에 연결되는 tanner 그래프를 사용한다. 반복마다 변수 노드는 연결된 체크 노드 중 하나의 메시지를 다른 노드로부터 수신된 모든 메시지에 기반한 체크 노드에 전송한다. 따라서 L 번 반복하는 BP 알고리즘은 완전히 연결된 DNN 구조에서 2L 개의 숨은 레이어로 펼쳐질 수 있으며, 각 숨은 레이어는 tanner 그래프의 가장자리를 나타내는 뉴런 수와 동일하다. 이 뉴런들은 해당 가장자리에서 전송된 메시지의 출력이 된다. 즉, 홀수(짝수) 레이어가 변수 노드로부터 체크노드까지 송신된 메시지를 출력한다. 기존의 알고리즘과 DNN 기반의 BP 알고리즘의 유일한 차이점은 tanner 그래프의 가장자리에 할당되는 것이다. 여기에서 메시지는 가중치가 있는 가장자리에 전파된다.
(그림 7)에서 제안된 DNN 기반의 BP 디코더에서 첫 번째 두 개의 레이어가 체크 노드가 첫 번째 반복에서는 어떠한 정보도 포함하지 않기 때문에 하나의 레이어로 병합되었다. DNN 기반의 BP 디코더는 본질적으로 비슷한 특성의 BP 속성을 보존하고, 그 성능은 송신된 코드워드에 독립적이다. 따라서 네트워크는 모든 선형 코드가 속하는 하나의 코드워드의 잡음 버전에 의해 학습될 수 있다.
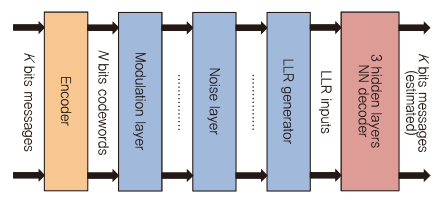
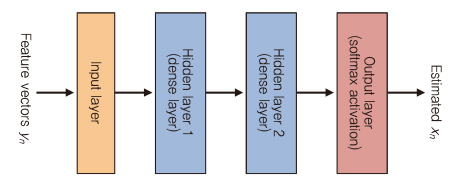
(그림 8)은 K개의 정보 비트를 가진 N 길이의 코드워드를 디코딩하기 위해 제안되었다[7]. N 길이의 인코딩된 코드워드는 모듈레이션 레이어와 통신 채널 효과를 나타내는 AWGN(Additive White Gaussian Noise) 채널 레이어를 통과한다. 그런 다음 잡음이 있는 코드워드의 LLR 정보는 K개의 정보 비트들을 출력하도록 학습시키는 3개의 숨은 레이어를 가진 네트워크의 N 차원 입력으로 만들어진다.
낮은 지연을 갖는 병렬 구조와 one-shot 디코팅은 채널 디코딩 알고리즘을 NN 디코딩이 대체 가능하게 만든다. 임의의 SNR을 갖는 코드워드를 분류하기 위한 학습의 최적 SNR이 존재하며, 더 많은 학습을 하는 것이 더 나은 결과를 가져올 수 있다. NN 디코딩에서 직접적인 채널 값 또는 손실 함수로써 mean squared error나 binary cross entropy를 사용하는 LLR을 통한 훈련은 최종 결과에 큰 영향을 미치지 않는다.
3. Detection
Massive MINO와 mmWave와 같은 통신 시스템은 증가하는 응용분야와 함께, 사용 가능한 통신 시나리오나 통신 채널이 점점 복잡해져가고 있으며 채널 모델의 계산 및 이에 대응하는 검출 알고리즘의 복잡성 또한 증가하고 있다. 일반적인 검출 알고리즘은 실시간으로 계산상의 병목 현상을 일으킨다.
딥러닝 방법은 충분한 표현력과 다루기 쉬운 매개 변수의 최적화로 인해, 채널 코딩과 유사한 특정한 반복 검출 알고리즘에 의한 검출과 유연한 레이어 구조의 영향으로 정확성과 복잡성 사이의 tradeoff로 사용될 수 있다. 데이터 검출은 네트워크를 통해 이루어지는 간단한 forward pass가 되며, 실시간으로 동작될 수 있다.
복잡한 채널 모델에도 불구하고, 수학적으로 다루기 쉬운 채널 모델은 매우 복잡한 경우(분자 통신, 수중 통신 등) 정확하게 물리적 전파 과정을 특징짓는 것에 사용될 수 없다. 따라서 채널 정보가 요구되지 않는 새로운 검출 방법에 대한 방법이 필요하다. 딥러닝은 표현력, 정의된 채널 모델의 불필요 및 end-to-end 성능을 최적화하는 능력 때문에 이 문제점에 대한 해결책이 될 수 있다.
딥러닝 기반의 검출기를 설계할 때, n번째 수신 신호가 n번째의 송신 신호 xn에 의해 결정되는 간단한 memoryless 시스템으로써 간주된다. Symbol-to-symbol 검출은 (그림 9)와 같이 완전히 연결된 DNN 구조로 구현될 수 있다[8].
Ⅳ. 새로운 통신 구조로서의 딥러닝
딥러닝 기반의 알고리즘은 전통적인 블록 구조를 갖는 통신 시스템 (그림 5)의 하나 또는 두 개 블록의 대안으로 제안되는 경우가 많았다. 그러나 기본적인 통신은 물리적인 통신 채널을 통해 한 지점에서 다른 지점으로 신호를 전파하고, 실용적인 채널 효과를 처리하고, 신뢰성을 확보하기 위해 송신기와 수신기를 사용한다. 따라서, 성능 향상은 두 개 혹은 그 이상의 블록을 함께 최적화함으로써 달성할 수 있기 때문에, 각 블록의 최적화는 통신에서의 전반적인 최적화를 보장할 수 없다.
1. Autoencoder-Based End-to-End System
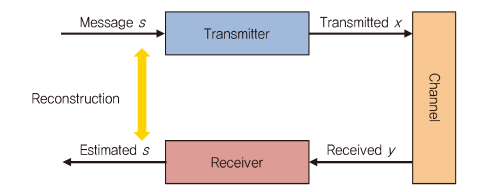
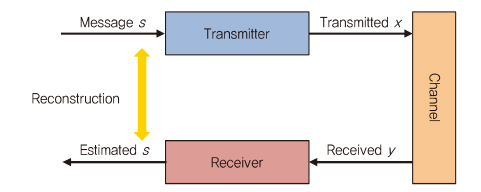
(그림 10)과 같이, 무선 통신 시스템은 송신된 메시지가 물리 채널을 통해 수신 단에서 재구성되는 end-to-end 시스템으로 간주된다. 따라서 autoencoder는 전체 통신 시스템을 표현할 수 있고, AWGN(Additive White Gaussian Noise) 채널에서 송신기와 수신기를 동시에 최적화할 수 있다. 원래의 autoencoder는 출력 레이어에서 입력을 재구성하는데 사용할 수 있는 압축된 형태의 입력을 학습하는 unsupervised DL 알고리즘이다.
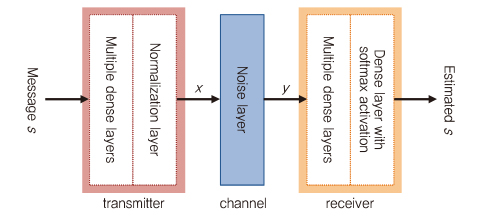
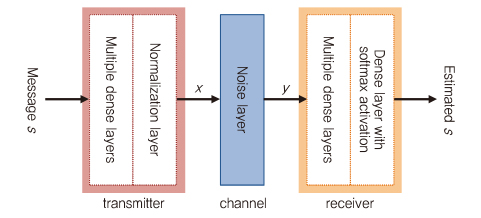
제안된 접근법에서 송신기와 수신기는 완전히 연결된 DNN으로 표시되는 반면, 송신기와 수신기 사이의 AWGN 채널은 약간의 변화를 가진 단순한 잡음 레이어로 표현된다. 통신 시스템을 불완전한 채널로 송신된 신호 x의 대표로써 전파 가능한 신호 중 하나인 s로부터 학습하는 커다란 autoencoder로 간주할 수 있다. 따라서 수신 측에서는 원래의 메시지를 수신된 신호 y로부터 학습하는 것으로 인하여 낮은 에러율을 갖는 estimated s를 재구성할 수 있다. 전체적인 autoencoder 기반의 통신 시스템은 BER(Bits Error Rate)나 BLER(Block Error Rate)와 같은 end-to-end 성능을 향상시키기 위해 학습된다[(그림 11) 참조], [4].
2. Autoencoder for Multi-user
Autoencoder 시스템이 보편적인 통신 구조로 사용되기 위해서는 간섭 채널을 갖는 다중 사용자 통신과 같은 복잡한 시나리오에서 구현 가능해야 한다.
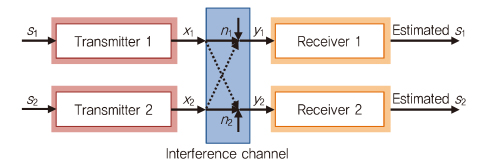
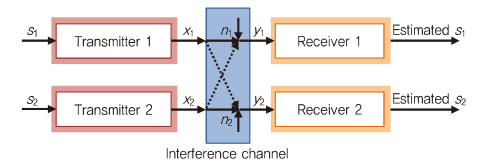
동시에 같은 간섭 채널에서 통신을 시도하는 두 명의 사용자를 갖는 통신 시스템을 (그림 12)와 같이 표현할 수 있다. 하나의 사용자를 갖는 경우와의 차이점은 전체 시스템이 수신기 쪽에서 간섭을 극복하도록 학습을 하는 점이다[4].
3. Autoencoder for MIMO
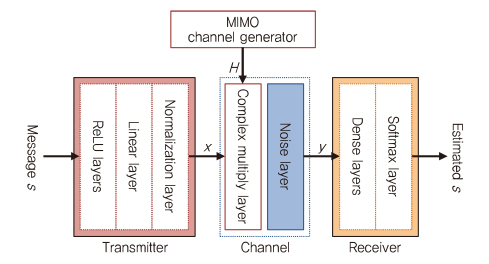
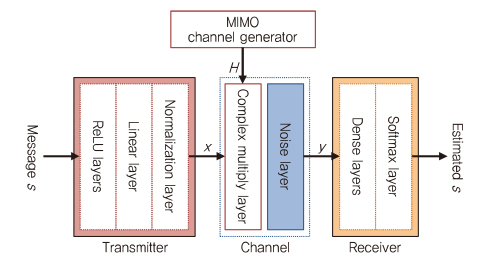
Autoencoder 통신 시스템은 (그림 13)과 같이 MIMO 채널까지 확장할 수 있다. 일반적인 MIMO 통신은 채널 상태 정보(CSI: Channel State Information) 피드백이 없는 개방형 시스템과 CSI 피드백이 있는 폐쇄형 시스템으로 고려될 수 있다. AWGN 채널과는 달리, MIMO 채널 응답(H)는 채널 네트워크 블록에 잡음을 추가하기 전에 임의로 생성된다[9].
CSI 피드백이 없는 개방형 autoencoder 시스템의 송신기는 메시지 s를 MIMO 채널 응답(H)에 해당하는 병렬 스트림으로 인코딩한다. 그런 다음 메시지는 수신된 신호 y를 생성하기 위해 잡음 레이어를 통과 하기 전에 미리 정의된 채널 응답(H)를 곱한다.
CSI 피드백이 있는 폐쇄형 autoencoder 시스템은 송신기가 수신기로부터 완벽한 CSI 정보를 얻을 수 있는 이상적인 상황이 고려된다.
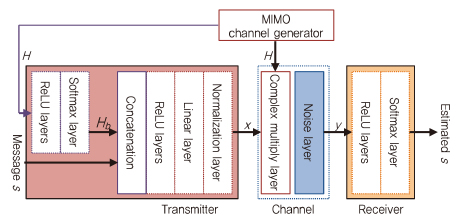
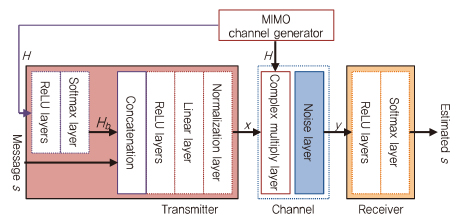
개방형 autoencoder 시스템과 비교하면, 폐쇄형 autoen-coder는 (그림 14)와 같이 일반적인 MIMO autoencoder 구조에 피드백이 추가된다. 채널 모듈에서 생성된 채널 응답(H)는 송신기 입력으로 사용하며, 이는 x로 인코딩되었던 메시지 s와 연결된다[9].
Ⅴ. 맺음말
본고에서는 무선 통신 시스템에서 일반적인 통신 시스템의 일부를 대체하거나, 새로운 딥러닝 기반의 구조로 제안되는 경우를 살펴보았다.
딥러닝 기반의 알고리즘의 탁월한 표현력과 편리한 최적화를 감안할 때, 기존의 이론에 도전하는 미래의 통신 시스템으로서의 잠재력이 크다. 아직 초기 단계인 무선 통신 시스템에서 물리 계층에 기계학습을 적용하는 것은 이론적인 분석과 실제 통신 환경에 보다 적합한 딥러닝 기반의 새로운 구조가 제안된다면, 극적인 발전과 다양한 활용이 가능할 것으로 예상된다.
약어 정리
ASR
Automatic Speed Recognition
AWGN
Additive White Gaussian Noise
BER
Bit-Error Rate
BLER
BLock Error Rate
BP
Belief Propagation
CNN
Convolutional Neural Network
CSI
Channel State Information
DL
Deep Learning
DNN
Deep Neural Network
GD
Gradient Descent
HDPC
High-Density Parity Check
LLR
Log-Likelihood Ratio
MIMO
Multi-Input Multi-Output
ML
Machine Learning
NLP
Natural Language Processing
NN
Neural Network
NND
Neural Network Decoder
ReLU
Rectified Linear Units
RNN
Recurrent Neural Network
SGD
Stochastic Gradient Descent
SNR
Signal-to-Noise Ratio
SVM
Support Vector Machine
UDN
Ultra-Densification Network
T. Wang, C.-K. Wen, H. Wang, F. Gao, T. Jiang, and S. Jin, “Deep Learning for Wireless Physical Layer: Opportunities and Challenges,” Oct. 2017, Accessed 2018. http://arxiv.org/abs/1710.05312v2
S. Dorner, S. Cammerer, J. Hoydis, and S. Brink, “Deep Learning-Based Communication Over the Air,” June 2017, Accessed 2018. http://arxiv.org/abs/1707.03384v1
T. O’Shea and J. Hoydis, “An Introduction to Deep Learning for the Physical Layer,” June 2017, Accessed 2018. http://arxiv.org/abs/1702.00832v2
A.K. Nandi and E.E. Azzouz, “Algorithms for Automatic Modulation Recognition of Communication Signals,” IEEE Trans. Commun., vol. 46, no. 4, Apr. 1998, pp. 431-436.
E. Nachmani, Y. Be’ey, and D. Burshtein, “Learning to Decode Linear Codes Using Deep Learning,” Annu. Allerton Conf. Commun, Contr. Comput., Monticello, IL, USA, Sept. 27-30, 2016, pp. 341-346.
T. Gruber, S. Cammerer, J. Hoydis, and S. Brink, “On Deep Learning-Based Channel Decoding,” Jan. 2017, Accessed 2018. http://arxiv.org/abs/1701.07738v1
N. Farsad and A. Goldsmith, “Detection Algorithms for Communication Systems Using Deep Learning,” July 2017, Accessed 2018. http://arxiv.org/abs/1705.08044v2
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.