딥러닝을 활용한 무선 전송 및 접속 기술 동향
Research Trends on Wireless Transmission and Access Technologies Using Deep Learning
- 저자
-
김근영미래이동통신연구본부 kykim12@etri.re.kr 명정호미래이동통신연구본부 jhmyung@etri.re.kr 서지훈미래이동통신연구본부 jihoon.seo@etri.re.kr
- 권호
- 33권 5호 (통권 173)
- 논문구분
- 일반논문
- 페이지
- 13-23
- 발행일자
- 2018.10.01
- DOI
- 10.22648/ETRI.2018.J.330502
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- Deep learning is a promising solution to a number of complex problems based on its inherent capability to approximate almost all types of functions without the demand for handcrafted feature extraction. New wireless transmission and access schemes based on deep learning are being increasingly proposed as substitutes for existing approaches, providing a lower complexity and better performance gain. Among such schemes, a communications system is viewed as an end-to-end autoencoder. The learning process applied in autoencoders can automatically deal with some nonlinear or unknown properties in communications systems. Deep learning can also be used to optimize each processing block for required tasks such as channel decoding, signal detection, and multiple access. On top of recent related research trends, we suggest appropriate research approaches for communications systems to adopt deep learning.
Share
Ⅰ. 머리말
전송 채널 용량의 이론적 한계를 제시한 C. Shannon의 중요한 업적 이후, 통신시스템은 발전을 거듭하여 그 활용 영역이 사람 간 통신을 넘어 사람과 기기, 기기 간 통신으로까지 확장되고 있다. 실제 통신 환경은 다수의 송수신기로 구성되어 복잡하게 얽혀 있지만, 현재 사용하고 있는 대부분의 무선 전송 및 접속 기술은 직교 방식의 자원 분배를 통해 다수 송수신기 환경을 단일 송수신기 환경으로 근사화하고 있다. 이러한 접근 방법은 송수신기를 좀 더 간단히 구현할 수 있다는 장점이 있지만, 자원을 나눠서 사용한다는 측면에서 비효율성 문제를 갖고 있다. 이러한 문제를 해결하고자, 다수 송수신기로 구성된 간섭 채널 환경에 적합한 전송 기술을 찾는 연구가 활발히 진행되고 있으나, 이론과 실제 구현 간 간격은 적지 않다.
그러나, 최근 딥러닝의 비약적 발전으로 인해 이론으로만 존재하는 방식을 실제 시스템에 도입할 수 있는 가능성이 제시되고 있다. 이미지 분류, 번역, 바둑, 자율주행 등에서 딥러닝이 보여준 놀라운 성능에 힘입어, 거의 모든 산업 분야에서 딥러닝 도입이 고려되고 있다. 통신 분야 역시 다양한 영역에서 딥러닝을 활용하는 방안이 연구되고 있다[1]-[6]. 본 논문에서는 먼저 딥러닝에 대한 핵심적인 내용을 살펴보고, 무선통신과의 연계성을 바탕으로 딥러닝을 무선통신기술에 적용할 때 고려해야 할 내용을 제안한다. 또한, 딥러닝을 무선전송 및 무선접속 기술에 활용한 최신 사례들을 소개한다.
Ⅱ. 딥러닝과 무선통신기술
1. 딥러닝 개요
딥러닝은 주어진 문제에 대한 경험을 통해 성능 향상을 도모하는 기계학습의 한 분야이다[7]. 기계학습은 지도학습, 비지도학습, 강화학습으로 구분된다. 지도학습은 입력과 정답으로 구성된 학습데이터를 이용한 학습을 통해, 학습데이터에 포함되지 않은 일반적인 입력에 대해서도 정답이 나오도록 일반화하는 것이 목적이다. 비지도학습은 정답이 없는 데이터에서 숨겨진 구조를 찾아내는 것이 목적이다. 강화학습은 동작주체의 행동과 동작에 대한 반응으로 주변환경에서 발생하는 보상과 상황변화라는 상호작용을 통해, 최적의 행동방침을 찾는 것이 목적이다[8]. 기계학습은 다양한 문제에 활용할 수 있으며, 활용 분야를 크게는 출력이 실수와 같은 연속 값을 구하는 것이 목표인지 또는 자연수와 같은 이산 값을 구하는 것이 목표인지 이 2가지로 구분할 수 있다. 연속 값을 구하는 것이 목표인 대표적인 분야가 변수 간의 적절한 관계를 구하는 회귀 추정이고, 이산 값을 구하는 것이 목표인 대표적인 분야가 분류이다. 통신 분야에서 다루어온 추정이론은 연속 값, 검출이론은 이산 값을 구하는 것이 목표인 분야에 대응된다고 볼 수 있다.
기계학습에서 다루는 대부분의 문제는 입력과 출력의 관계로 표현되며, 출력에 영향을 미치는 요인이지만 미처 고려하지 못한 입력, 혹은 우리가 제어할 수 없는 잡음 등에 의해 발생하는 오류를 더하여 이 입력과 출력의 관계를 y = f(x) + ε과 같은 함수로 표현할 수 있다. 따라서, 기계학습은 제한된 학습데이터를 통해 알려지지 않은 입력과 출력 간 관계, 즉 f(x)를 추정하는 함수 근사화로 볼 수 있다[9]-[11]. 통신시스템을 포함하여, 자율 주행, 그림 분류, 번역 등 대부분의 문제가 함수로 표현될 수 있으며, 기계학습의 역할을 함수 근사화로 볼 수 있기 때문에, 광범위한 분야에 기계학습을 적용할 수 있다.
기계학습이 주어진 문제를 얼마나 해결하는지를 판단하기 위한 대표적인 성능척도로 기계학습의 출력과 정답과의 오차 값이 사용될 수 있다. 일반적으로는 학습데이터에 대해서는 이 오차 값을 ‘0’으로 만드는 것이 가능하지만, 학습데이터로 사용하지 않은 데이터에 대해서는 제어할 수 없는 오류로 인해 이 오차 값을 ‘0’으로 만드는 것이 대부분 불가능하다. 이 오차 값을 최소화하는 것이 기계학습이 해결해야 하는 숙제이며, 여기에서 Bias-Variance Tradeoff 문제가 발생한다. 학습에 사용하지 않은 데이터에 대한 오차 값은 정답과 기계학습의 출력 차이(즉, Bias), 매번 적용되는 데이터의 차이에서 기인하는 변화량(즉, Variance)과 오류의 합으로 표현할 수 있다. 우리가 해결하려는 문제에 지나치게 단순한 기계학습 모델을 사용하면 Bias는 커지고, Variance는 작아지게 되는 과소적합(underfitting)이 발생하고, 과도하게 복잡한 기계학습 모델을 사용하면 Bias는 작아지고 Variance는 커지는 과적합(overfitting)이 발생한다. 일반적으로는 문제 해결을 위해 충분히 복잡한 모델을 사용하기 때문에 과적합이 발생하며, 이를 해결하기 위한 접근법들을 정규화(regularization)라 한다. 과적합은 기계학습이 학습데이터에 포함된 오류까지 학습한다거나, 복잡한 모델을 충분하지 않은 수의 데이터로 학습한다거나, 학습데이터와 실제로 적용되는 테스트데이터가 다를 경우 등 다양한 원인에서 발생한다고 볼 수 있다.
딥러닝 역시 기계학습의 일종이므로 간단히 표현하면 함수 근사화라고 할 수 있다. 딥러닝은 함수 근사화를 위해, 입력에 대해 비선형 처리를 담당하는 은닉층을 2개 이상 두어 출력을 내도록 하는 방식을 사용한다. 입력과 출력을 제외한 은닉층이 굳이 2개 이상인 경우를 딥러닝이라 하는 것은 비선형 처리를 하는 유닛(hidden unit)이 충분하다면 하나의 은닉층만으로도 거의 모든 함수 근사화가 가능하다는 universal approximation 이론에서 기인한다[12], [13]. Universal approximation 이론에 의하면 2개 이상의 은닉층이 필요 없는 듯하지만, 여러 개의 은닉층을 쌓으면 계산 효율성 향상, 계산에 필요한 유닛 수 감소 등 여러 가지 장점이 생기기 때문에 현재는 수백 개의 은닉층을 쌓기도 한다.
딥러닝에서 사용하는 인공신경망은 Deep Feedforward Network(DFN), Convolutional Neural Network(CNN), Recurrent Neural Network(RNN)로 구별된다[14]. DFN은 입력이 비선형 계산 과정을 거쳐 다음 계층으로 전달되는 동작이 피드백 없이 순차적으로 수행된다. 선형 계산이 아닌 비선형 계산이 필요한 이유는 각 계층에서 연산이 선형 계산으로만 구성되어 있다면 여러 층의 계산 과정을 표현하는 여러 matrix 들을 곱하는 과정들이 하나의 matrix로 표현 가능하기 때문에 여러 층을 쌓는 의미가 없어지기 때문이다. DFN은 딥러닝의 가장 기본적인 형태이며, 각 계층의 유닛들이 모두 연결되어 있는 구조를 가지고 있다. CNN은 각 계층 입력에 대해 convolution 연산이 들어간다. 이러한 convolution 연산은 모든 유닛을 연결하지 않고 특정 유닛 일부만 연결(sparse connection)하고, 연산에 필요한 파라미터를 동일하게 사용(parameter sharing)하고, 입력 값의 위치 이동에 대해 동등한 출력(equivalent representation)이 가능하게 하여 복잡도를 낮추면서, 동시에 성능을 높이게 된다. RNN은 연속되는 데이터 간 상관성을 활용하기 위해 은닉층에 피드백 연결을 둔다.
딥러닝 학습은 정답과 인공신경망 출력 차이로 정의된 손실함수 값에 대해서 학습데이터로 평균치를 구하고 이를 최소화하는 gradient descent 방식을 사용한다. Gradient descent 방식은 최솟값을 구하기 위해, 함수에 사용되는 각 파라미터에 대한 편미분 값을 구하고, 이와 반대되는 방향으로 파라미터를 갱신하여 손실함수 값이 최솟값으로 수렴하도록 하는 방식이다. 손실함수가 ‘0’으로 수렴하게 되면 정답과 인공신경망의 출력 값과 차이가 없다는 것을 의미하나, 학습데이터에 사용하지 않은 데이터에 대한 일반화 성능이 떨어지는 과적합 문제가 발생하기 때문에 이를 해결하기 위해서는 다양한 정규화 방식을 적절히 활용해야 한다.
2. 딥러닝과 무선통신 간 연계성
딥러닝과 이동통신은 많은 부분에서 유사한 점이 있다. 예를 들어, 많은 통신 문제는 입력신호(x)가 무선채널(H)을 통과하고, 가우시안 잡음(n)이 더해지는 수신신호(y)로 모델링된다. 즉, y = Hx + n는 이동통신에서 가장 많이 활용하는 수학적 모델로, 기계학습에서 활용하는 y = f(x) + ε 와 동일한 형태이다. 또한, 딥러닝에서 손실함수 값을 최소화하는 방식이 통신의 추정이론에서 사용하는 MMSE(Minimum Mean Square Error)를 최소화하는 것과 일치하며, 이는 적절한 변환을 통해 채널부호화에서 최적 복호 방식인 최대 사후 확률 방식과도 일치한다.
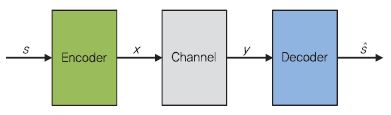
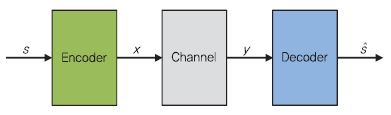
통신시스템을 송신기에서 전송한 신호를 수신기에서 오류없이 그대로 복구하는 형태로 해석한다면, 딥러닝 기법 중 하나인 종단 간 autoencoder로 볼 수 있다[15], [(그림 1) 참조]. 통신시스템을 종단 간 autoencoder로 해석한다면, 통신시스템에서 발생하는 비선형 오류 및 부분 최적화가 아닌 전체 최적화를 위한 수학적 모델링을 통하지 않고, 딥러닝 학습과정을 통해 최적의 방식을 도출하도록 할 수 있다.
통신시스템에서 다루는 문제는 딥러닝 등 기계학습에서 다루어 왔던 기존 문제들에 비해 장점을 가지고 있다. 사회/자연 현상 등 일반적인 문제의 경우, 최적의 해를 정의하기도 쉽지 않고, 학습데이터를 얻기도 쉽지 않다. 그러나, 통신시스템은 전송하는 신호조차도 자연에서 주어지는 것이 아니라 우리가 원하는 대로 생성하며, 신호가 전송되는 채널도 수학적으로 잘 모델링되어 있으며, 수신기에서 출력해야 할 최적의 해가 무엇인지 알 수 있는 경우가 대부분이다. 통신시스템은 잘 모델링된 환경에서 동작하며, 최적의 해를 정의할 수 있기 때문에, 이를 통해 입력과 정답으로 구성된 학습데이터를 원하는 만큼 충분히 얻을 수 있다. 하지만, 전송하려는 데이터가 수십~수백 비트만 되더라도, 단순한 학습과정으로는 감당하기 어려울 정도의 복잡도를 가지게 된다. 예를 들어 부호율 1/2로 100비트의 정보를 보내려고 하는 경우, 200차원의 공간에 2의 100승에 해당하는 어마어마한 코드워드 수가 존재한다. 따라서, 모든 코드워드를 활용하여 학습하는 것은 어려운 일이며, 최적 성능에 근접하면서도 높은 성능을 내도록 하는 효율적인 학습 방안이 필요하다.
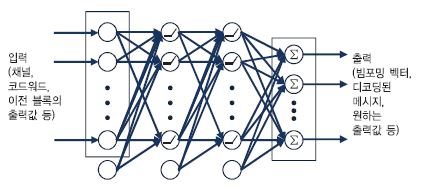
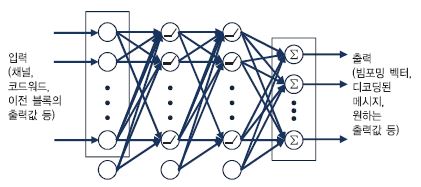
통신시스템을 종단 간 autoencoder로 해석하는 방식 대신, 통신시스템의 일부 블록을 딥러닝을 활용하여 구현할 수 있다. 일반적으로 통신시스템은 채널부호화, 변복조, 빔포밍 등 여러 개의 처리 블록이 연결된 시스템으로 볼 수 있다. 딥러닝을 한마디로 표현하면 함수 근사화라고 할 수 있으며, 통신시스템의 각 블록은 입력에 대해 원하는 출력이 나오도록 하는 함수로 볼 수 있기 때문에 각 블록을 딥러닝을 이용하여 구현할 수 있다[(그림 2) 참조].
딥러닝을 활용하여 통신시스템의 각 블록을 구현하려고 하는 경우, 기존 통신시스템에서 충분히 성능을 달성하고 있는 경우라면 딥러닝을 적용했을 경우 이점이 적다. 예를 들어, 단일 송수신기 환경에서는 기존 통신시스템이 감당 가능한 복잡도 내에서 거의 최적 성능을 달성하고 있으며, 딥러닝을 활용하더라도 더 좋은 성능을 달성하기 쉽지 않다. 하지만, 다수 송수신기가 데이터를 전송하는 간섭채널 등 현재 통신시스템이 충분한 성능을 내지 못하는 통신 환경이라면, 딥러닝 도입을 고려할만 하다.
현재 통신시스템은 간섭을 회피하기 위해 자원을 나누어 사용하는 직교 방식의 전송 방식을 채택하고 있다. 이는 다수 송수신기 통신환경에서 간섭 처리를 용이하게 하기 위해, 자원을 겹치지 않게 할당하는 직교 방식을 통해 다수 송수신기 환경을 여러 쌍의 단일 송수신기 환경으로 모사한 것으로 볼 수 있다. 하지만, 이론적 한계에 도달하는 최적 성능을 달성하기 위해서는, 직교 방식이 아닌 다수 송수신기가 동일 자원을 동시에 사용하여 송수신하는 비직교 방식을 활용해야 한다. 비직교 통신 방식의 경우, 현재 통신 시스템에 적용하기에는 복잡도가 매우 높은 경우가 대부분이며, 딥러닝을 활용하면 현재의 통신 시스템보다 좋은 성능 달성을 기대할 수 있다. 높은 복잡도로 인해 달성하기 어려운 non-convex 문제가 있다면, 컴퓨터를 통해 구한 해를 이용하여 학습데이터를 구성하여 딥러닝 학습에 이용할 수 있다. 컴퓨터를 통해 데이터를 구하기 때문에 학습 데이터를 원하는 만큼 충분히 얻을 수 있다. 또한, 학습 단계에서는 많은 시간이 걸릴 수 있으나 학습이 끝난 인공신경망을 실제 시스템에서 활용하는 단계에서는 행렬 곱셈과 비선형 함수를 적용하는 단순한 연산이 반복되므로, 딥러닝을 실제 통신시스템에 적용하는 것도 문제가 없을 것으로 판단된다.
딥러닝 등 기계학습을 통신 문제 해결에 이용하려 할 때 다음과 같은 고려사항들이 존재한다[15].
먼저 학습/검증 데이터에 관한 것이다. 기계학습 모델과 알고리즘의 성능을 비교하기 위해서는 일반적인 검증방법과 공개된 데이터 셋을 확보하는 것이 중요하다. 컴퓨터 비전, 음성 인식, 자연어 처리 등의 분야에서는 상기 사항이 만족되었지만, 통신 분야에서의 기계학습 활용에 있어서는 아직 그러지 못하다. 앞서 언급한 분야에서는 특정 상황들에 대한 데이터를 사용해야 하지만, 통신 분야에서는 의도한 대로 정확하게 만들어진 신호가 사용되기 때문에, 통신을 위한 기계학습의 학습/검증 데이터 생성 방법 등을 표준화/일반화 할 수 있는 가능성이 존재한다. 예를 들어, [16]에서는 변복조 분류 문제에 대한 신호 생성 소프트웨어와 데이터 셋을 제공하고 있다.
데이터 표현법, 손실 함수, 학습 SNR(Signal-to-Noise Ratio)에 대해서도 고민이 필요하다. 통신 분야에서 기계학습 활용은 비교적 새로운 연구 주제이기 때문에, 최적의 데이터 표현법, 손실 함수, 학습 방법이 어떤 것인지 아직 알려지지 않았다. 예를 들어, 이진 신호는 이진 또는 one-hot 벡터, 변조된 심볼, 정수 등으로 표현될 수 있으며, 신경망 구조, 학습 목표, 손실 함수 등의 요소에 따라 최적 표현법이 다를 수 있다. 예를 들어 채널 디코딩 문제에서는 신경망의 입력으로 채널 관측값을 사용할 수도 있고, LLR(Log-Likelihood Ratio)을 사용할 수도 있다. 그리고 학습 SNR 에 대해서는, 기계학습 기반 통신 시스템이 어떤 특정한 SNR에서 학습되어야 하는지에 대한 명쾌한 해답은 없는 상태이다. 학습이 완료된 시스템이 학습된 SNR과 관계없이 모든 SNR 에서 잘 동작한다면 좋을 것이다. 하지만 [15]에 따르면, 특정 SNR 또는 SNR 범위에서 학습을 했다고 해서, 다양한 SNR 또는 SNR 범위에서의 검증/테스트 성능이 항상 우수하게 나오는 것은 아니었다. 예를 들어, 낮은 SNR에서 학습을 수행한 경우, 높은 SNR에서의 예측에 중요한 요소인 코드 구조가 학습되지 않았다. [17]에서는 먼저 높은 SNR에서 학습하고 학습를 진행하면서 학습 SNR을 점차적으로 낮췄을 때 성능이 뚜렷하게 증가함을 보였다. 이와 관련하여 어떤 손실 함수를 선택해야 하는지에 대한 문제도 존재한다. [15]에서는 통신에서의 분류 문제를 기계학습으로 해결하려고 했기 때문에, 분류 문제에 주로 쓰이는 categorical cross-entropy를 손실 함수로 사용하였지만, 다른 데이터 표현법에 대해서는 다른 손실 함수를 선택하는 것이 좋을 수 있다. 또한, 적합하지 않은 손실함수를 선택할 경우 좋지 못한 성능을 얻을 수 있기 때문에, 손실함수 선정에 유의해야 한다.
복소수 값 처리에 대한 고민도 필요하다. 통신에서는 기저대역에서 복소수 표현을 사용하기 때문에 많은 신호처리 과정에서 위상 회전, 켤레 복소수, 복소수의 크기 등을 다룬다. 이러한 이유로, 통신 문제에 사용되는 인공신경망도 실수보다는 복소수를 다루는 것이 더 바람직할 것이다[18]. 하지만 현재까지 알려진 기계학습 라이브러리는 복소수를 지원하지 않는다. 이 문제에 대한 해결책으로는 Wirtinger calculus가 사용될 수 있다[19].
Ⅲ. 딥러닝 활용 무선전송 기술 동향
1. 종단 간 autoencoder로 본 무선전송기술
Autoencoder(AE)는 비지도학습 딥러닝의 한 예로, 입력값과 출력값이 일치하도록 신경망이 학습되는 특징을 가지고 있다. 통신 시스템을 종단 간에서 송신된 메시지를 수신기에서 그대로 재구성하는 시스템으로 보면, 딥러닝 관점에서 무선 통신 시스템은 AE의 한 유형으로 볼 수 있다[14, (14 장) 참조].
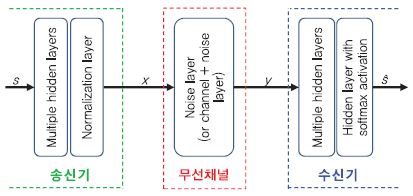
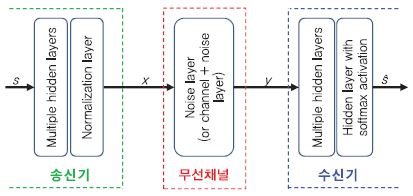
(그림 3)은 무선 통신 시스템에 딥러닝 기술이 적용된 종단 간 AE 구조를 보여준다[15]. 전달 메시지 s는 송신기에서 다계층 신경망과 정규화 계층을 걸쳐 송신 신호 x로 변환되고, 무선 채널을 통과한 뒤 잡음이 더해져 y라는 신호로 수신기에 전송된다. 수신기는 수신된 y를 다계층 신경망과 softmax 활성 함수로 구성된 계층에 통과시켜 0과 1 사이의 확률 값으로 변환하고, 이 값을 토대로 전달 메시지 s 값을 예측(s ̂)하는 과정을 수행한다. AE 신경망은 평균제곱오류나 binary cross-entropy 손실 함수를 이용하여 입력 s와 예측 값 s ̂의 오차를 줄이는 방향으로 학습이 진행되며, 이에 따른 결과로 블록오류율이 작아지는 종단 간 성능 향상을 얻을 수 있다. 본 연구는 기존 다양한 블록들(채널 인코딩, 변/복조, 채널 디코딩 등)로 구성된 무선 통신 구조를 종단 관점에서 재구성할 수 있다는 가능성을 제시하고, 딥러닝을 기반으로 전체 최적화를 수행하는 새로운 통신 구조의 모습을 보여준다.
AE 관련 연구결과는 간섭채널로도 확장할 수 있다. [15]에서는 두 개의 송수신기 쌍으로 이루어진 간섭채널에서 AE의 성능을 보여준다. 기존 단일 송수신기 쌍에서의 학습방법과 다른 점은, 자신의 신호는 잘 예측하면서 간섭 신호는 극복할 수 있도록 학습이 진행된다는 점이다. 학습의 결과로 두 개의 송신기는 두 수신기가 신호를 서로 구별하기 쉽게 변조하여 신호를 전송하고, 수신기는 구별된 신호 중 자신의 신호를 찾아 전달 메시지를 예측하여 성능 향상을 얻는다.
또한, AE는 MIMO 환경에서도 적용될 수 있다. [20]에서는 다양한 MIMO 채널 피드백 환경에서 AE 성능을 보여준다. 기존 AE 학습과 다르게, 학습 입력으로 채널 정보가 들어가는 것이 특징이다. 해당 채널 정보는 수신기에서 측정한 채널 값이 v개의 비트로 양자화되어 피드백을 통해 송신기로 전달되며, 채널 피드백 정보 역시 학습 과정을 통해 전송된다. MIMO 기반으로 학습된 AE는 안테나별 송신 전력의 불균등한 분배를 통해 일종의 중첩 코드 성질을 갖게 되어 공간 다이버시티를 얻을 수 있을 뿐 아니라, 신호 mapping과 de-mapping 과정에서 시간/공간 영역에서 오류정정 기능을 내재하게 됨으로써 더 좋은 BER 성능을 얻을 수 있다.
그 외에, [21]에서는 실제 채널에서 AE 사용을 위하여, 확률적 채널 모델을 통한 일반 AE 학습 및 실제 채널에서 성능 향상을 위한 미세조정 AE 학습의 두 단계 학습 기법을 제안한다. 여기서 미세조정 AE 학습은 전송 주파수 오프셋, 샘플링 타임/주파수 오프셋 등과 같이 하드웨어 불완전성으로 발생하는 변수들을 학습하는 과정을 의미한다. [22]에서는 네트워크 구조(DNN, CNN) 및 다양한 손실 함수와 활성 함수에 따른 AE의 성능 결과를 보여준다.
2. 채널 디코딩 기술
디코딩 문제에 단순한 심층 순방향 네트워크(DFN)를 사용하는 것을 넘어서, 다른 딥러닝 기법을 이용하는 연구들이 진행되었다. [23]에서는 다음과 같은 다양한 기법들이 제안되었다.
• Neural Belief Propagation(BP) Decoder: BP 디코더의 일반화 버전
• Neural Min-Sum Decoding: Neural BP 디코더에 Min-Sum 근사를 적용하여 계산 복잡도 감소
• BP-RNN 디코더: Neural BP 디코더의 가중치에 RNN 관련 제한사항 추가
• Learning to Relax: BP의 성능을 향상시키기 위해 사용되는 Successive relaxation[24] 기법을 Neural BP 디코더에 적용
• mRRD-RNN 디코더: HDPC 코드 디코딩을 위한 mRRD(modified Random Redundant iterative algorithm)에 Neural BP 디코더를 적용
[25]에서는 일반적인 BP 디코더와 CNN을 결합하고 이를 반복적인(Iterative) 방식으로 활용하는 Iterative BP-CNN 아키텍처를 제안하였으며, [26]에서는 선형 블록 코드의 디코딩에 RNN을 활용하는 기법을 제안하였다. 그리고 [27]에서는 MLP(Multi-Layer Perceptron), CNN, RNN 세 가지 신경망 디코더의 성능을 비교하기 위해, 세 가지 신경망 디코더의 파라미터 수가 비슷해지도록 각각의 레이어 수, 각 레이어의 노드 수를 조정하였을 경우, 셋 중에서는 RNN 이 가장 높은 성능을 보였지만 복잡도가 높으며, CNN은 MLP 보다 약간 더 복잡하지만 좋은 성능을 내었다고 소개하였다.
3. 딥러닝을 활용한 신호검출 및 채널 추정 기술
가. 신호검출 기술
딥러닝은 신호처리 분야, 특히 MIMO 적용시 발생하는 복잡한 신호 처리를 해결하는 방안으로 점점 더 주목을 받고 있다. [28]에서는 DNN이 MIMO 채널에서 송신 신호를 잘 예측할 수 있도록, DetNet이라는 MLP기반 신호 검출 네트워크를 제안하였다. MIMO 신호 검출에 사용하는 AMP와 SDR 알고리즘과 성능을 비교할 경우, DetNet이 AMP보다 항상 좋은 성능을 보였으며 SDR과 유사한 성능을 제공한다. [29]에서는 MIMO-OFDM 시스템에서 신호를 분류하는 수단으로 딥러닝을 사용했다. 제안된 기법은 신호의 특성 불변성을 고려한 AE 기반 특징 추출기와 extreme learning machine을 사용하여 신호를 구별하도록 학습을 수행한다. 해당 기법의 성능은 여러 가지 전통적인 방법과 비교해 더 높은 탐지 정확도를 달성한다 [29]. 그 외로, 저해상도 ADC를 가진 MIMO 시스템에서 수신 채널 정보가 없는 상황에서도 지도 학습을 통한 송신 신호 검출 방법[30], Massive overloaded MIMO 시스템에서 성긴/희소 신호 복구를 위한 딥러닝 기반 반복적 신호 검출 알고리즘[31], MIMO DF relay 채널에서 딥러닝을 활용한 신호 검출 알고리즘[32]이 제안되었다. 또한, 입력과 출력 사이의 복잡한 관계를 근사할 수 있는 딥러닝의 특징을 이용하여, 수학적 통신 채널 모델링이 없는 분자 통신 분야에서의 딥러닝 기반 신호 검출방법도 연구되고 있다[33].
나. 채널 추정 기술과 피드백 기술
다중 안테나를 사용하는 무선 통신 시스템에서 채널추정 정확도를 높이기 위한 pilot 수 증가와 그에 따른 채널 추정 복잡도 문제는 다중 안테나 시스템을 활용하는 데 큰 걸림돌로 인식되고 있다. 딥러닝은 이러한 문제를 해결하는 좋은 해결방안 중 하나가 될 수 있다.
[34]에서는 OFDM 송수신기에서 딥러닝을 활용한 채널 추정 및 신호 검출 기능을 구현하였다. 해당 기법은 채널 통계 기반 시뮬레이션에서 생성된 데이터를 사용하여 딥러닝 학습을 오프라인으로 수행하고, 해당 학습 결과물을 온라인 OFDM 시스템의 신호 복구 블록에 적용하여 채널 왜곡을 바로잡고 신호를 복구하는 특징을 가지고 있다. 제안 기법은 채널 추정을 위한 pilot 수가 충분한 경우(64개)에는 기존 기술들과 비슷한 BER 성능을 보이지만, pilot 수가 줄어든 경우(8개) 성능 열화가 나타나는 다른 기술들과 달리 월등히 좋은 성능을 보여준다. 또한, 데이터 오버헤드로 작용하는 CP를 사용하지 않는 OFDM 시스템에서도 가장 좋은 성능을 얻는 것을 확인하였다. 해당 연구 결과는 딥러닝을 통한 채널 추정 및 신호 검출 방법이 무선 통신 시스템의 pilot 수 문제 해결과 전송 데이터 효율을 올릴 수 있는 좋은 해법이 될 수 있음을 보여준다.
그 외에 딥러닝을 활용한 또 다른 채널 추정 관련 기술로, [35]에서는 uniform linear array로 구성된 massive MIMO 환경에서 학습을 통한 저복잡도 채널 필터를 디자인하는 기법을 소개하였고, [36]에서는 CsiNet이라는 딥러닝 네트워크를 만들어 채널을 추정하고 압축 센싱 기반으로 채널 피드백 데이터를 생성/복구하는 기술을 제안하여 Massive MIMO 환경에서 효율적인 채널 피드백을 수행하는 시스템을 제안하였다.
Ⅳ. 딥러닝 활용 무선접속 기술 동향
1. 비직교 접속기술
5G 이동통신 기술에서 요구되는 저지연, 대규모 연결을 만족하기 위해, 서로 중복되지 않는 자원을 할당하여 접속하는 기존의 직교 접속 기술 대신, 비직교 접속 기술이 제안되고 있으며, 대표적인 기술로 SCMA가 있다[37]-[39]. SCMA는 채널 부호화기에서 나오는 정보 비트를 미리 정의된 코드북을 통해 다차원 복소수 코드워드로 바로 전환하여 전송함으로써 신호 형태의 효율성에서 이득을 얻는 기술이다. 사용자 혹은 안테나 별로 다른 코드북을 구성하여 전송함으로써 다수 사용자 및 데이터 전송이 가능하다. 또한, 0이 아닌 요소의 개수가 적은 성긴 코드(sparse code)를 사용하기 때문에, 적은 수의 무선자원에 다수 데이터를 동시에 전송하더라도 신호들이 충돌할 가능성이 적어지고, factor graph를 이용한 메시지 전달 알고리즘을 통해 거의 최적의 복호 성능을 달성할 수 있다. 그러나, 다차원 복소수 코드워드를 사용하기 때문에 좋은 코드북을 제시하기가 쉽지 않고, 메시지 전달 알고리즘의 반복연산 때문에 복잡도가 높다. 이 문제를 해결하기 위해, 심층인공신경망을 사용할 수 있다[40]. [40]에서는 코드북 생성과 복호를 위해, denoising AE를 제안하였다. 제안된 기법은 다수의 심층인공신경망을 사용하여 코드북을 생성하고, 전체 무선자원에 산재된 정보를 연결하는 심층인공신경망을 통한 복호를 특징으로 한다. 이를 통해, 심층인공신경망이 인간을 대신하여 복잡한 코드북을 생성할 수 있고, 저복잡도로 더 좋은 성능을 달성할 수 있음을 보였다.
비직교 접속 방식의 또 다른 대표적인 기술로 사용자별 채널 상황에 따라 다른 크기의 전력을 할당하는 NOMA가 있다[41], [42]. NOMA에서는 동일한 무선자원에서 전송률 혹은 공평성에 따라 사용자별로 전력을 할당하여 전송하고, 수신기에서는 SINR(Signal-to-Interference-Plus-Noise Ratio) 크기가 감소하는 순으로 간섭신호를 제거하여 수신한다. NOMA에서는 사용자별 서로 다른 채널 상황이나, 서로 다른 전력 할당에 따른 신호 세기 차이를 통해, 동시에 신호를 전송하여 이득을 얻게 된다. 그러나 높은 복잡도와 더불어, 채널이 급격하게 변하는 상황에서는 사용하기 어렵다는 단점이 있다. 이러한 문제를 해결하고자, [43]에서는 채널 특성을 자동적으로 검출하기 위해 LSTM에 기반한 딥러닝 방식을 제시하였다. 제안된 기법에서는 시뮬레이션을 통해 얻은 데이터를 offline에서 학습시키고, 실제 입력에 대응되는 출력이 online 학습 과정을 통해 산출된다. 딥러닝을 통해 부호 및 복호화, 채널 추정을 자동적으로 수행하게 되며, 기존 방식에 비해 우수한 성능 달성이 가능함을 시뮬레이션을 통해 보였다.
2. 전력제어 및 할당 기술
높은 성능 달성을 위해 무선통신시스템은 전력제어 및 할당 기술을 이용한다. 전력제어 및 할당 기술은 일반적으로는 최적화 문제를 통해 유도되며, 간단한 형태의 해가 존재하기 않기 때문에, 대신 반복적 계산을 통해 해를 구한다. [44]에서는 일반적으로 사용되는 복잡한 weighted minimum mean square error 기반 전력제어 방식에 근사하는 해를 도출하기 위해 인공신경망을 활용하였다. 근사 오류는 심층인공신경망의 계층과 노드 수에 의존한다는 것이 제시되었으며, 인공신공망을 활용하여 전력제어 구현시, 저복잡도로 구현 가능하기 때문에 실시간으로 자원할당이 가능하다.
[45]에서는 주파수 또는 에너지 효율을 높이기 위한 CNN기반 전력제어 방식을 제시하였다. [44]에서는 기존 전력제어 방식으로 달성할 수 있는 성능에 도달하기 위해 심층인공신경망을 사용하였기 때문에, 기존 성능을 능가하는 성능 달성이 불가능하지만, [45]에서는 CNN을 통해 국부적인 채널정보를 분산적으로 활용하더라도 저복잡도로 기존 방식에 근접하거나 높은 성능을 낼 수 있다는 것을 제시하였다.
[46]에서는 단일 안테나를 가진 다수 개의 단말이 통신하는 간섭채널에서 심층인공신경망을 활용하여 전송률을 높이기 위한 전력제어 방식을 제안하였다. 이러한 간섭채널의 경우 최적 전력 할당 방식이 알려져 있지 않기 때문에, 전송률을 최대화하기 위해 비지도 학습 방식을 이용하였으며, 저복잡도로 기존의 모든 전력제어 방식보다 더 높은 성능을 달성할 수 있음을 제시하였다.
[47]에서는 다중 안테나를 가지는 다수 개의 단말이 통신하는 간섭채널에서 인공신경망을 활용하여 전력제어를 하는 송신기와 간섭제거를 하는 수신기 구조를 제시하였다.
Ⅴ. 맺음말
딥러닝과 통신시스템은 많은 유사점을 가지고 있다. 딥러닝은 제한된 데이터를 통해 입력과 출력의 상관도를 추정하는 함수 근사화로 볼 수 있으며, 대부분의 통신시스템 역시 입력과 출력의 함수 관계로 표현할 수 있다. 그리고, 통신시스템은 딥러닝이 적용되기에 좋은 이점을 갖고 있다. 통신시스템에서 전송되는 신호는 자연적으로 주어지는 것을 사용하는 것이 아니라 우리가 원하는 대로 생성할 수 있다. 일반적으로 통신시스템은 잘 정의된 모델링 환경에서 동작하기 때문에 최적의 해를 정의할 수 있고, 이를 이용하여 입력과 출력으로 구성된 학습데이터를 원하는 만큼 충분히 얻을 수 있는 장점을 갖고 있다.
그 동안 눈부신 발전을 거듭하여 온 통신시스템이지만, 다수 송수신기로 구성된 통신환경에서 간섭 문제 극복이나, 최적 채널 부호화 방식 등 아직까지 해결되지 못한 문제들이 많이 남아 있다. 이러한 영역에 딥러닝을 이용하여 기존에 달성하지 못했던 성능을 보여준다면, 통신시스템은 기존과는 전혀 다른 새로운 방식으로 그동안 이루지 못했던 획기적인 성능 달성이 가능하지 않을까 예상해 본다.
약어 정리
ADC
Analog-to-Digital Converter
AE
Autoencoder
AMP
Approximate Message Passing
BER
Bit Error Rate
BLER
Block Error Rate
BP
Belief Propagation
CNN
Convolutional Neural Network
CP
Cyclic Prefix
CSI
Channel State Information
DF
Decode-and-Forward
DFN
Deep Feedforward Network
DNN
Deep Neural Networks
ELM
Extreme Learning Machine
HDPC
High Density Parity Check
LLR
Log-Likelihood Ratio
LSTM
Long-Short-Term Memory
MIMO
Multiple-Input and Multiple-Output
MLP
Multi-Layer Perceptron
MRRD
modified Random Redundant iterative algorithm
MSE
Mean Squared Error
NND
Neural Network Decoder
NOMA
Non-Orthogonal Multiple Access
OFDM
Orthogonal Frequency-Division Multiplexing
RNN
Recurrent Neural Network
SCMA
Sparse Code Multiple Access
SDR
Semidefinite Relaxation
SINR
Signal-to-Interference-Plus-Noise Ratio
SNR
Signal-to-Noise Ratio
T. Wang et al., “Deep Learning for wireless Physical Layer: Opportunities and Challenges,” China Commun., vol. 14, no. 11, Nov. 2017, pp. 92-111.
C. Wang, P. Patras, and H. Haddadi, “Deep Learning in Mobile and Wireless Networking: A Survey,” eprint arXiv: 1803.04311, Mar. 2018.
Q. Mao, F. Hu, and Q. Hao, “Deep Learning for Intelligent Wireless Networks: A Comprehensive Survey,” IEEE Commun. Surveys Tutorials, Early Access, June 2018.
M. Chen et al., “Machine Learning for Wireless Networks with Artificial Intelligence: A Tutorial on Neural Networks,” eprint arXiv: 1710.02913, Oct. 2017.
X. You et al., “AI for 5G: Research Directions and Paradigms,” eprint arXiv: 1807.08671, July 2018.
Z. Qin et al., “Deep Learning in Physical Layer Communications,” eprint arXiv: 1807.11713, July 2018.
R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction (2nd Edition), MIT Press: Cambridge, MA, USA, 2018.
G. James et al., An Introduction to Statistical Learning: with Applicationsin R, Springer: New York, USA, 2014.
T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Springer: New York, USA, 2016.
G. Cybenko, “Approximation by Superpositions of a Sigmoidal Function,” Math. Contr., Signals, Syst., vol. 2, no. 4, Dec. 1989, pp. 303-314.
K. Hornik, “Approximation capabilities of multilayer feedforward networks,” Neural Netw., vol. 4, 1991, pp. 251-257.
I. Goodfellow, Y. Bengio, and A. Kourville, Deep Learning, MIT Press: Cambridge, MA, USA, 2016.
T.J. O’Shea and J. Hoydis, “An Introduction to Deep Learning for the Physical Layer,” IEEE Trans. Cognitive Commun. Netw., vol. 3, no. 4, 2017, pp. 563-575.
D. George and E.A. Huerta, “Deep Neural Networks to Enable Real-Time Multimessenger Astrophysics,” Phys. Rev. D, vol. 97, no. 4, 2018, Article no. 044039.
A. Hirose, Complex-Valued Neural Networks, Springer Science & Business Media: Berlin, Germany, 2012.
M.F. Amin et al., “Wirtinger Calculus Based Gradient Descent and Levenberg-Marquardt Learning Algorithms in Complex-Valued Neural Networks,” In B.L. Lu, L. Zhang, and J. Kwok (eds), Lecture Notes in Computer Science, vol 7062, Springer: Berlin, Heidelberg, 2011.
T. O’Shea, T. Erpek, and T. C. Clancy, “Deep Learning Based MIMO Communications,” arXiv preprint arXiv: 1707.07980, 2017.
S. Drner et al., “Deep Learning-Based Communication Over the Air,” Asilomar Conf. Signals, Syst. Comput., vol. 12, no. 1, Oct. 2017, pp. 1791-1795.
T.J. O’Shea, K. Karra, and T. C. Clancy, “Learning to Communicate: Channel Auto-Encoders Domain Specific Regularizers and Attention,” in IEEE Int. Symp. Signal Process. Inform. Technol., Limassol. Cyprus, Dec. 12-14 2016, pp. 223-228.
E. Nachmani et al., “Deep Learning Methods for Improved Decoding of Linear Codes,” IEEE J. Sel. Topics Signal Process., vol. 12, no. 1, 2018, pp. 119–131.
S. Hemati and A.H. Banihashemi, “Dynamics and Performance Analysis of Analog Iterative Decoding for Low-Density Parity-Check (LDPC) Codes,” IEEE Trans. Commun., vol. 54, no. 1, Jan. 2006, pp. 61–70.
F. Liang, C. Shen, and F. Wu, “An Iterative BP-CNN Architecture for Channel Decoding,” IEEE J. Sel. Topics Signal Process., vol. 12, no. 1, 2018, pp. 144–159.
E. Nachmani et al., “RNN Decoding of Linear Block Codes,” arXiv preprint arXiv: 1702.07560, 2017
W. Lyu et al., “Performance Evaluation of Channel Decoding With Deep Neural Networks,” in IEEE Int. Conf. Commun. (ICC), Kansas, MO, USA, May 20-24, 2018, pp. 1–6.
N. Samuel, T. Diskin, and A. Wiesel, “Deep MIMO Detection,” in IEEE Int. Workshop Signal Process. Adv. Wireless Commun. (SPAWC), Sapporo, Japan, July 3-6, 2017, pp. 690-694.
X. Yan et al., “Signal Detection of MIMO-OFDM System Based on Auto Encoder and Extreme Learning Machine,” in Int. Joint Conf. Neural Netw. (IJCNN), Anchorage, AK, USA, May 14-19, 2017, pp. 1602-1606.
Y.-S. Jeon, S.-N. Hong, and N. Lee, “Blind Detection for MIMO Systems with Low-Resolution ADCs Using Supervised Learning,” Proc. IEEE Int. Conf. Commun. (ICC), Paris, France, May 21-25, 2017, pp. 1-6.
M. Imanishi, S. Takabe, and T. Wadayama, “Deep Learning-Aided Iterative Detector for Massive Overloaded MIMO Channels,” arXiv preprint arXiv: 1806.10827, 2018.
X. Jin and H. Kim, “Deep Learning Detection Networks in MIMO Decode-Forward Relay Channels,” arXiv preprint arXiv: 1807.09571, 2018.
N. Farsad and A. Goldsmith, “Detection Algorithms for Communication Systems Using Deep Learning,” arXiv preprint arXiv: 1705.08044, 2017.
H. Ye, G.Y. Li, and B.-H.F. Juang, “Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems,” IEEE Wireless Commun. Lett., vol. 7, no. 1, Feb. 2018, pp. 114-117.
D. Neumann, W. Utschick, and T. Wiese, “Deep Channel Estimation,” in WSA, Berlin, Germany, Mar. 15-17, 2017, pp. 1–6.
C.-K. Wen, W.-T. Shih, and S. Jin, “Deep Learning for Massive MIMO CSI Feedback,” IEEE Wireless Commun. Lett., Early Access, 2018.
H. Nikopour and H. Baligh, “Sparse Code Multiple Access,” in IEEE Annu. Int. Symp. Personal, Indoor, Mobile Radio Commun. (PIMRC), London, UK, Sept. 8-11, 2013, pp. 332-336.
M. Taherzadeh et al., “SCMA Codebook Design,” in IEEE Veh. Technol. Conf. (VTC2014-Fall), Vancouver, Canada, Sept. 14-17, 2014, pp. 1-5.
Y. Wu et al., “Sparse Code Multiple Access for 5G Radio Transmission,” in IEEE Veh. Technol. Conf. (VTC-Fall), Toronto, Canada, Sept. 24-27, 2017, pp. 1-6.
M. Kim et al., “Deep Learning-Aided SCMA,” IEEE Commun. Lett., vol. 22, no. 4, Apr. 2018, pp. 720-723.
Y. Saito et al., “Non-Orthogonal Multiple Access (NOMA) for Cellular Future Radio Access,” IEEE Veh. Technol. Conf. (VTC Spring), Dresden, Germany, June 2-5, 2013, pp. 1-5.
L. Dai et al., “Non-Orthogonal Multiple Access for 5G: Solutions, Challenges, Opportunities, and Future Research Trends,” IEEE Commun. Mag., vol. 53, no. 9, Sept. 2015, pp. 74-81.
G. Gui et al., “Deep Learning for An Effective Non-Orthogonal Multiple Access Scheme,” in IEEE Trans. Veh. Technol., Early Access, 2018.
H. Sun et al., “Learning to Optimize: Training Deep Neural Networks for Wireless Resource Management,” eprint arXiv: 1705.09412, Oct. 2017.
W. Lee, M. Kim, and D. Cho, “Deep Power Control: Transmit Power Control Scheme Based on Convolutional Neural Network,” IEEE Commun. Lett., vol. 22, no. 6, June 2018, pp. 1276-1279.
H. Sun et al., “Learning to Optimize: Training Deep Neural Networks for Wireless Resource Management,” eprint arXiv: 1705.09412, Oct. 2017.
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.