브레인 모사 인공지능 기술
Brain-Inspired Artificial Intelligence
- 저자
-
김철호사이버브레인연구실 kimcheolho@etri.re.kr 이정훈사이버브레인연구실 jhlee0914@etri.re.kr 이성엽사이버브레인연구실 sylee549@etri.re.kr 우영춘사이버브레인연구실 ycwoo@etri.re.kr 백옥기사이버브레인연구실 ok.baek@etri.re.kr 원희선사이버브레인연구실 hswon@etri.re.kr
- 권호
- 36권 3호 (통권 190)
- 논문구분
- 일반논문
- 페이지
- 106-118
- 발행일자
- 2021.06.01
- DOI
- 10.22648/ETRI.2021.J.360311
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- The field of brain science (or neuroscience in a broader sense) has inspired researchers in artificial intelligence (AI) for a long time. The outcomes of neuroscience such as Hebb’s rule had profound effects on the early AI models, and the models have developed to become the current state-of-the-art artificial neural networks. However, the recent progress in AI led by deep learning architectures is mainly due to elaborate mathematical methods and the rapid growth of computing power rather than neuroscientific inspiration. Meanwhile, major limitations such as opacity, lack of common sense, narrowness, and brittleness have not been thoroughly resolved. To address those problems, many AI researchers turn their attention to neuroscience to get insights and inspirations again. Biologically plausible neural networks, spiking neural networks, and connectomebased networks exemplify such neuroscience-inspired approaches. In addition, the more recent field of brain network analysis is unveiling complex brain mechanisms by handling the brain as dynamic graph models. We argue that the progress toward the human-level AI, which is the goal of AI, can be accelerated by leveraging the novel findings of the human brain network.
Share
Ⅰ. 서론
뇌과학(Brain Science) 또는 보다 넓은 의미로 신경과학(Neuroscience)은 기계학습(Machine Learning) 및 인공지능(AI: Artificial Intelligence) 연구에 지속적인 영감을 주었다[1]. 초기의 AI 연구는 뇌과학이 도출한 결과를 모사하는 것에 중점을 두었으나, AI 기술의 성숙도와 복잡도가 점점 높아짐에 따라 그 모사의 정도가 희미해져 왔고, 최근 딥러닝을 비롯한 AI 첨단기술은 뇌과학과 뚜렷하게 구분되는 독자적인 영역을 구축하고 있다[1].
하지만 지난 10여 년간 AI 분야의 비약적인 발전을 주도했던 딥러닝 기반 기술은 최근 계산 측면에서 한계(Computational Limit)에 도달하고 있을 뿐 아니라[2], 블랙박스 성질에 의한 불투명성(Opacity), 보편 학습에 대한 취약성(Lack of Common Sense), 학습 영역에 대한 협소성(Narrowness), 환경 변화에 대한 불안정성(Brittleness) 등 주요 한계점들이 아직 근본적으로 해결되지 않고 있다[3,4].
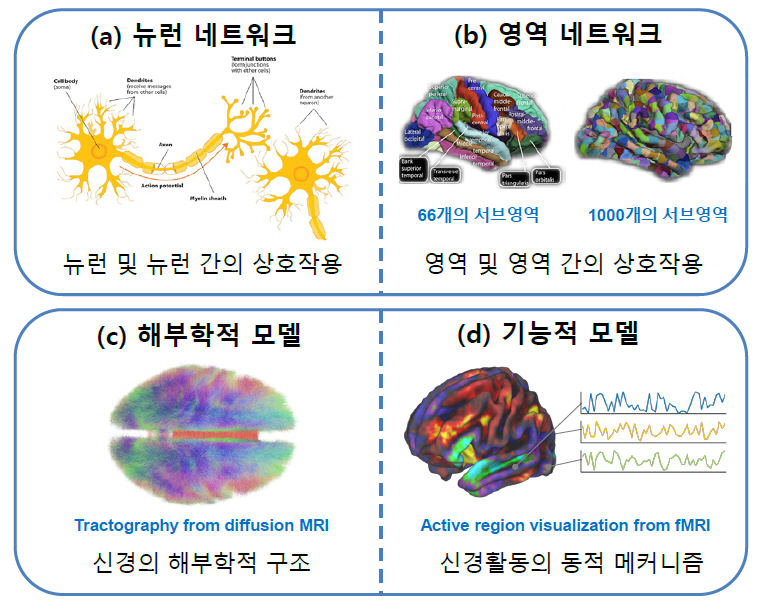
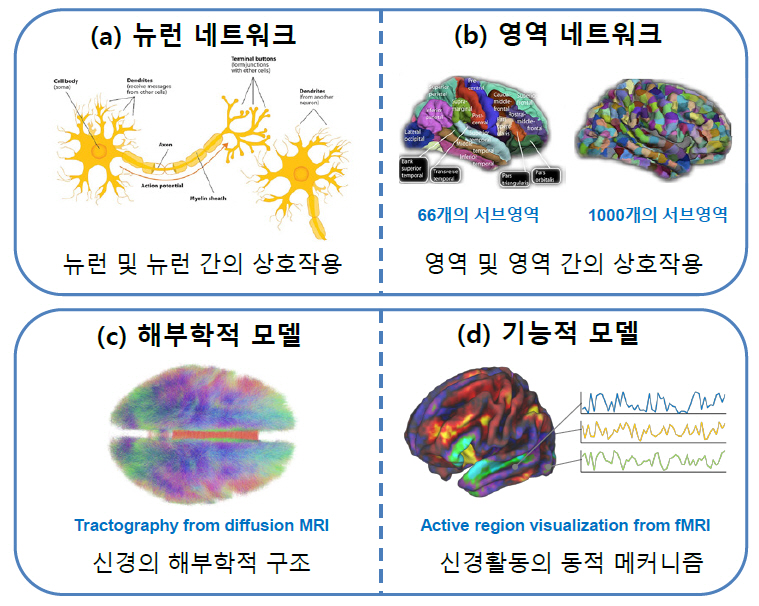
AI 기술이 마주한 이러한 한계를 효과적으로 해결하기 위해 뇌과학적 원리를 보다 구체적으로 모사하려는 연구가 활발히 진행되고 있다[1]. 뇌는 인간의 경우 약 1천억 개의 뉴런으로 이루어진 매우 복잡하면서도 역동적인 기관이기 때문에 모사의 관점이 매우 다양할 수밖에 없다. 우선 개별적인 뉴런의 기작으로부터 출발하려는 마이크로스케일의 뉴런 네트워크(Neuronal Network)(그림 1(a)) [5]와 뇌를 유의미한 영역으로 나누어 이들의 역동적 결합으로 이해하려는 메조스케일 또는 매크로스케일의 영역 네트워크(Regional Network)(그림 1(b))[6] 관점이 존재한다. 한편 뉴런이나 뇌 영역의 물리화학적 구조에 대한 해부학적(Anatomical) 모사(그림 1(c))[7]와 그들의 작동방식에 대한 기능적(Functional) 모사(그림 1(d))[8]로 나눌 수도 있다.
그림 1
브레인 모사의 다양한 관점
출처 뉴런 네트워크[5] CC BY-SA 4.0, 영역 네트워크[6] CC BY 3.0, 해부학적 모델[7] CC BY-SA 4.0, 기능적 모델[8] CC BY-NC 2.0 개작.
본 고에서는 이러한 다양한 뇌 모사의 관점에서 AI 기술을 고찰하고, 뇌를 어떠한 방식으로 모사하여 인간의 지적 수준에 보다 가까운 AI를 실현하고자 하는지 살펴보고자 한다.
Ⅱ. 심층신경망(DNN)
1. 초기 모델
가. 최초의 신경 모델
1871년 미국의 의사 Henry Bowditch는 근육에 전기 자극을 주었을 때 근육이 일정 강도를 넘는 자극에 대해서만 수축한다는 사실을 발견했다. “전부-전무 법칙(All-or-None Law)”으로 알려진 이 현상을 통해 자극에 대한 신경세포(뉴런)의 반응을 최초로 확인하게 되었다[9].
1943년에는 전부-전무 법칙의 이진성을 기반으로 뉴런 간의 신호 전달 과정을 반영한 최초의 인공신경 모델인 McCulloch-Pitts 모델이 발표되었는데[10], 이는 뉴런의 자극과 반응 특성이 간단한 논리 연산을 통해 모사될 수 있음을 시사하는 것이었다. 하지만 이 모델은 뉴런 간 시냅스의 연결 강도를 포함하지 않았고, 목적에 따라 뉴런의 문턱값(Threshold)을 일일이 정해 주어야 했기 때문에 학습이 가능한 수준에는 미치지 못했다.
나. 뉴런의 학습 모델
뉴런의 학습 메커니즘에 대한 최초의 이론은 1949년 캐나다의 심리학자인 Donald Hebb에 의해 제시되었다[11]. “함께 활성화된 뉴런은 서로 연결된다(Neurons that fire together wire together).”라고 알려진 Hebb의 법칙은 인접한 두 뉴런이 동시에 반복적으로 활성화되면 뉴런 간 시냅스의 연결 강도가 강화된다는 가설을 바탕으로 한다. Hebb의 법칙에 의한 모델은 학습에 의한 뉴런의 강화 현상만을 다루기 때문에 쉽게 발산한다는 단점이 있다. 이를 해결하기 위해 1981년 세 명의 과학자(Elie Bienenstock, Leon Cooper, Paul Munro)가 뉴런의 약화 현상까지 포섭하는 (자신들의 이름을 딴) BCM 이론을 제창하였고[12], 1982년에는 핀란드의 컴퓨터 과학자 Erkki Oja가 시냅스의 연결 강도에 제한을 가하는 방식으로 개선된 모델을 제시하였다[13]. 뉴런의 학습에 대한 이들 이론은 뇌의 생물학적 현상을 설명하기 위한 것이었지만 인공신경망 연구에도 지속적인 영감을 부여해왔다.
다. 퍼셉트론
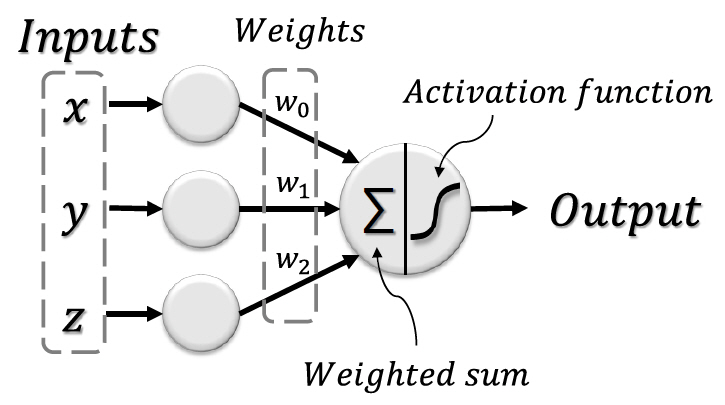
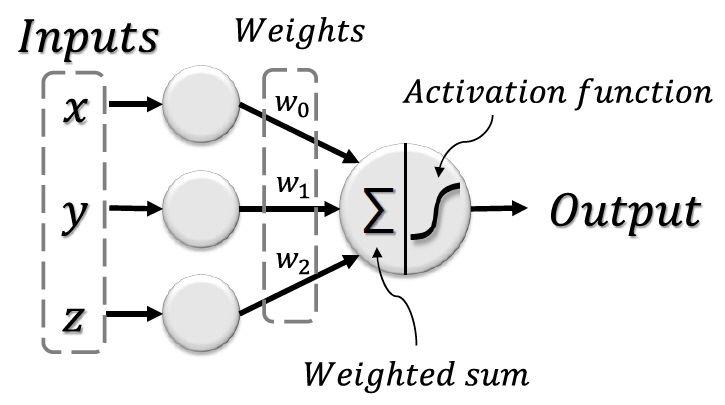
1958년 미국의 심리학자인 Frank Rosenblatt는 이진 데이터에 대해서만 적용이 가능했던 McCulloch-Pitts 모델과 달리 실수 데이터에 대해서도 적용이 가능한 새로운 뉴런 모델인 퍼셉트론을 제안한다[14]. 퍼셉트론은 그림 2와 같이 연결 강도를 나타내는 가중치를 통해 기존 모델에 비해 더 복잡한 학습이 가능했기 때문에 많은 기대를 불러 모았다[15].
하지만 초기 퍼셉트론 모델의 학습은 가중치의 초기값에 영향을 많이 받아 학습이 오래 걸리거나 보편적으로 적용하기 어려운 해를 도출하는 경우가 많고, 비선형 문제를 풀기 어렵다는 한계가 있었다[16].
라. 신경망의 발전
1982년 미국의 물리학자 John Hopfield는 전자의 스핀 모델에서 착안한 Hopfield망을 제안했다. Hopfield망은 Hebb의 법칙에 기반하여 가중치를 결정하고 네트워크의 상태에 대해 정의된 에너지가 점점 낮은 에너지에 도달한다는 조건을 만족하도록 학습이 진행되는데[17], 네트워크의 기억용량이 너무 작다는 한계가 있었다. 1984년 영국 출신의 컴퓨터 과학자 Geoffrey Hinton은 뉴런의 이진 출력을 Boltzmann 분포 기반의 확률로 표현한 Boltzmann machine을 제안하여 보다 정교한 학습이 가능하게 하였다[18]. 이후 2000년대 중반 Hinton은 Boltzmann machine의 뉴런 간 연결에 제한을 가하여 학습의 효율성을 높인 Restricted Boltzmann Machine(RBM)을 제안하였고, 이를 여러 층 쌓아 학습의 용량을 증대시킨 심층신뢰망(Deep Belief Network)으로 발전시켰다[19]. 심층신뢰망은 현재 널리 쓰이는 심층신경망과 같이 여러 층의 은닉층이 존재하는 구조를 가진다.
이렇듯 초기의 인공신경망은 뉴런의 해부학적 특징과 연결성을 모사함으로써 시작되었지만, 이후 실용적이고 효율적인 학습을 위해 확률이론 및 수학적 최적화, 컴퓨터공학적 기법에 기반하여 발그림 2 퍼셉트론의 모식도 전했다.
2. 심층신경망
가. 심층신경망
이른바 ‘딥러닝’이라고도 불리는 심층신경망(DNN: Deep Neural Network)은 앞서 언급한 다양한 신경망 알고리즘에 그 뿌리를 두고 있으며, 1980년대 Hinton에 의해 제안된 역전파(Backpropagation)를 비롯한 다양한 수학적 기법들과 결합하는 발전을 거듭하며 2000년대부터 현재까지 AI 분야를 주도하고 있다.
나. 심층신경망에 반영된 생물학적 특징
심층신경망은 많은 성취를 이루었지만 그와 동시에 여러 가지 한계를 드러냈고, 생물학적 특징을 간접적으로 적용하여 그 한계를 극복하고자 하였다. 대표적인 예로 콘볼루션 신경망(CNN)은 대뇌 시각피질의 다층 구조를 모사한 것으로서 컴퓨터 비전(Vision) 분야에 비약적인 발전을 가져왔다[1]. 전이학습(Transfer Learning)과 연속학습(Continual Learning) 또한 새로운 학습을 시도할 때 이전에 학습한 내용을 잊어버리는 파국적 망각(Catastrophic Forgetting)[20]의 한계를 극복하기 위해 생물학적 뇌가 과거에 구축한 지식을 토대로 새로운 학습에 적응하는 특성을 반영한 기법들이다. 이 밖에 몇 가지 사례만으로도 효과적으로 학습하는 뇌의 특성을 반영한 one-shot 또는 few-shot 학습 알고리즘[21], 뇌의 장단기 기억 메커니즘을 순차적 데이터 처리에 활용한 LSTM(Long Short-Term Memory) 알고리즘[22], 뇌가 입력된 정보의 특정 영역에 집중하는 현상에 착안한 주목(Attention) 알고리즘[23] 등이 있다.
이러한 시도는 학습 모델의 예측 성능 향상에 기여했지만 뇌의 생물학적 특징을 피상적으로 모사한 것으로서, 다음 절에서 다룰 심층신경망의 생물학적 비근사성(Biological Implausibility)을 근본적으로 해결하지는 못했다.
3. 심층신경망의 생물학적 비근사성
심층신경망 기술의 많은 아이디어는 뇌과학에서 파생되었지만, 그 이후 더 나은 성능을 위해 생물학적 근사성(Biological Plausibility)보다는 수학적, 컴퓨터공학적 기법에 의존해왔고, 그 결과 실제 뇌의 작동 방식과는 다른 점이 많다. 이 절에서는 AI 모델에서 생물학적 근사성이 가지는 의미에 대해 설명하고, 역전파를 중심으로 현재 인공신경망에 존재하는 생물학적 비근사성에 대해 기술할 것이다.
가. 생물학적 근사성이 가지는 의미
뇌는 ‘지능’의 가장 확실한 증거이며, 인간의 경우 단 20와트의 에너지로 고도의 지적 기능을 수행할 수 있는 매우 효율적인 기관이다[1]. 따라서 생물학적 근사성을 추구하는 것은 인간 수준의 기능을 궁극적 목표로 하고 있는 AI 기술의 발전에 있어 신뢰할 수 있는 접근 방식이며, 앞 절에서 언급하였듯이 AI 기술은 이를 통해 많은 성과를 거두어 왔다.
생물학적 근사성에 대한 추구는 뇌과학 측면에서도 의미가 있다. 빅데이터를 기반으로 한 인공신경망 기술이 뇌의 메커니즘에 관한 연구에 활용될 수 있으며[24], 이는 더 나아가 뇌에 대한 제어를 통해 질병을 치료하는 데에도 응용될 수 있다.
나. 역전파에 존재하는 비근사성
역전파는 딥러닝의 핵심 요소이지만 생물학적 근사성 측면에서 다음과 같은 문제가 있다.
1) 가중치 전달 문제
가중치의 미분을 이용한 역전파 알고리즘에서는 포워드 연산에 사용하는 가중치와 피드백 연산에 사용하는 가중치가 동일해야 한다[25]. 하지만 실제 뇌의 포워드와 피드백 과정에는 각각 다른 시냅스가 참여하기 때문에 상호 간의 정보를 전달하기 어렵다. 이를 ‘가중치 전달 문제(Weight Transport Problem)’라고 한다.
2) 활성화 함수의 도함수 전달 문제
인공신경망에서 노드의 입력과 출력을 연결하는 활성화 함수는 대개 비선형 함수이며 모든 노드는 같은 함수를 이용한다. 여기에 역전파 알고리즘을 이용하여 특정 노드에 대한 가중치의 미분값을 구하기 위해서는 그 노드에 도달하기까지 거쳐간 모든 노드의 활성화 함수에 대한 도함수가 필요하다. 하지만 실제 뇌에서는 뉴런의 활성화 함수가 서로 조금씩 다른 경우가 많기 때문에 역전파를 이용하는 경우 이러한 상이함을 고려해야 하는데[26], 그 차이를 실질적으로 어떻게 반영하는가에 대한 방법은 아직 확립되지 않았다.
3) 선형 연산
역전파 알고리즘에서의 피드백 연산은 선형 연산이지만 실제 뉴런은 비선형 연산을 포함한다. 역전파의 피드백 연산에는 이러한 비선형 연산을 보상할 수 있는 추가적인 장치가 없다. 비슷한 문제가 포워드 연산에서도 존재하는데, 노드의 입력에서 이전 노드들의 출력을 합할 때, 뉴런의 출력을 합하는 과정에 존재하는 비선형성을 고려하지 않는다[27].
다. 기타 비근사성
심층신경망에는 역전파 알고리즘에 관련된 것 이외에도 몇 가지 생물학적 비근사성이 존재한다. 우선 입력값의 정밀도에 차이가 있는데, 인공신경망에서 전달되는 값들은 연속적이지만 실제 뉴런의 연산은 이산값을 가지는 스파이크를 통해 이루어진다. 또한, 일반적으로 입력에 존재하는 시간적 차이를 다루지 않거나 간접적으로 다루는 DNN에 비해 실제 뉴런은 입력 스파이크의 타이밍, 빈도 등을 통해 정보를 전달한다[28].
학습 방식에 존재하는 차이도 있다. 인공신경망에서는 출력 계산을 위한 포워드 연산과 업데이트를 위한 피드백 연산이 명확히 구분되어 있다. 하지만 실제 뉴런에서는 이 두 가지가 동시다발적으로 일어난다. 또한, 대부분의 DNN은 정답이 주어지는 지도학습 방식에 기반하는데, 뇌에서도 실제로 지도학습이 일어나는지, 일어난다면 정답은 어떤 방식으로 주어지는지 아직 충분히 밝혀지지 않았다[26].
4. 생물학적 근사성을 반영한 인공신경망
인공신경망에 존재하는 여러 생물학적 비근사성을 해결하거나 완화하기 위한 연구가 많이 진행되고 있다. 이 절에서는 기존 딥러닝 프레임워크상에서 이를 다루는 접근법에 대해 살펴본다.
가. 지역적 학습 알고리즘
앞서 언급한 바와 같이 역전파를 통한 개별 노드의 학습을 위해서는 노드 전반에 대한 전역적인 정보(Global Information)가 필요한데, 이는 지역적인 정보(Local Information)로 학습을 하는 생물학적 뉴런과 상이한 특성이다. 최근 인공신경망에서는 이러한 역전파의 생물학적 비근사성에서 벗어나 생물학적 뉴런과 같이 지역적 학습(Local Learning)을 할 수 있는 모델에 대한 연구가 시도되고 있다.
최근의 한 연구는 피드백 연산에서 무작위 가중치 행렬을 사용하더라도 인공신경망의 학습이 가능하다는 것을 입증하였다[25]. 무작위 가중치 행렬에 대한 정보는 피드백을 통해 결국 포워드 가중치에 전달되고, 포워드 가중치가 피드백 가중치와 정렬되는 방향으로 업데이트되면서 점차 유용한 오차 정보가 모델에 반영되는 것이다. 이러한 방식은 대형 데이터 세트에 적용하기는 어렵지만 역전파 알고리즘에 대한 새로운 가능성을 열어주었고, 포워드와 피드백 연산 시 사용하는 가중치의 부호를 동기화 하거나[29], 가중치 정렬 기능을 향상시키는[30] 등의 연구가 추가로 진행되고 있다.
이 밖에도 시간적 혹은 공간적 차이로 인한 노드 활성화 값의 변화를 통해 학습을 이룰 수 있다는 이론도 있다[24]. 이는 여러 층의 노드가 모두 마지막 출력에 대한 오차를 보고 순차적으로 학습하는게 아니라, 각 층으로 전달된 정보를 통해 지역적 정보만을 활용한 업데이트가 가능하다는 것이다. 물론 아직 이러한 방식으로 일반적 딥러닝 수준의 성능을 낼 수 있는 건 아니지만 최근 뇌과학 연구의 발전에 힘입어 생물학적 근사성에 대한 검증이 진행되며 지속적으로 발전하고 있다.
나. 양자화 신경망
일반적으로 인공신경망에서의 연산은 실수값(32 혹은 64 비트)에 기반하지만 실제 뇌의 시냅스는 이에 비해 적은 1~5비트 사이의 정밀도를 가진다고 알려져 있다[31]. 따라서 인공신경망이 필요로 하는 정밀도를 낮추는 연구가 많이 진행되고 있는데, 이를 양자화 신경망(ONN: Quantized Neural Network)이라고 한다[32-34].
QNN은 모델의 성능은 유지하면서 모델이 요구하는 정밀도는 최대한 낮추는 것을 목표로 한다. 이를 위해 학습 과정에서 사용되는 값들을 저장 가중치, 전파 가중치, 활성화 값, 미분값 등으로 세분하고, 목적에 따라 서로 다른 정밀도로 다룬다. 예를 들어 서버와의 통신 부하를 최소화하기 위해 피드백 과정에서 전파되는 미분 값만을 2비트로 양자화한 연구[32], 모바일 디바이스의 부하를 최소화하기 위해 포워드 과정에서 전파되는 가중치 및 활성화 값을 1비트로 양자화한 연구[33], 범용성을 위해 전반적인 정밀도를 8비트 이하로 양자화한 연구[34] 등이 있다.
다. 하이브리드 구조
생물학적 근사성이 높은 인공신경망을 기존의 딥러닝 기반 신경망과 결합하여 훨씬 단순한 구조로 효율적인 성능을 도출하고자 하는 하이브리드 방식의 접근 방법이 있다. 자율주행 시스템을 위한 최근의 한 연구[35]는 이미지 데이터의 특성을 추출하는 콘볼루션 신경망의 출력에 예쁜꼬마선충의 뉴런을 모사한 NCP(Neural Circuit Policy) 네트워크를 연결하는 방식을 통해 기존 CNN 기술 대비 63배나 간소한 시스템으로 최고 수준의 성능을 달성하였다. 이 하이브리드 네트워크는 뛰어난 주행 정확도를 보일 뿐 아니라 기존 기술 대비 입력의 변화나 잡음에 대해 강인하고 부드러운 주행을 가능하게 하였다. 이러한 하이브리드 방식은 생물학적 근사성을 도입하여 딥러닝 기반의 네트워크의 성능을 증강시킬 수 있는 효과적인 방법이라 할 수 있다.
Ⅲ. 스파이킹 신경망(SNN)
앞서 소개한 바와 같이 심층신경망에 생물학적 근사성을 반영하려는 다양한 시도가 이루어지고 있지만, 이들은 입력되는 정보를 시간적인 신호로 처리하는 뉴런의 중요한 특성을 고려하지 않았다. 이 절에서는 이러한 뉴런의 생물학적 특징을 모사하는 스파이킹 신경망(SNN: Spiking Neural Network)에 대해 다루고자 한다.
1. 스파이킹 신경망의 코드화
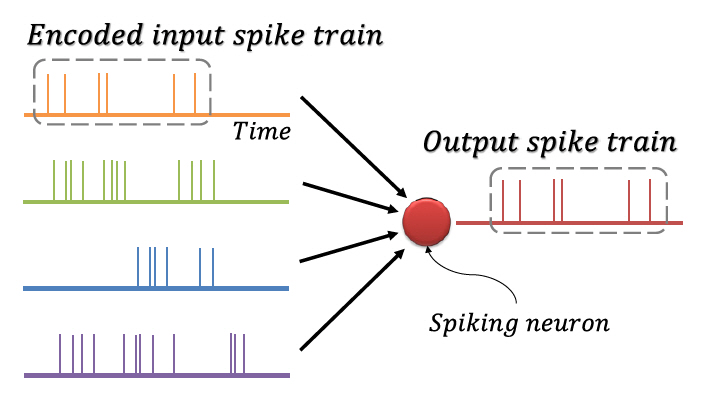
뉴런 간의 신호전달은 활동전위(Action Potential)에 의한 이산적 스파이크를 통해 일어나며, 시간에 따라 지속적으로 발생하는 스파이크를 스파이크열(Spike Train)이라 한다. 뉴런에 입력되는 정보가 스파이크열의 시간적 구성에 담긴다는 사실이 관찰되었는데[36,37], 이를 반영하기 위해 그림 3에 도식화한 것과 같이 정보를 이진의 스파이크열로 코드화(Encoding)하여 처리하는 방식의 스파이킹 신경망이 고안되었다. 코드화 기법에는 스파이크 발생 빈도를 이용하는 빈도 코드화(Rate Coding), 스파이크의 발생 시각을 이용하는 시각 코드화(Temporal Coding), 첫 스파이크를 이용하는 TTFS 코드화(Time-To-First Spike Coding), 짧은 시간 안에 집중적으로 발생한 스파이크를 이용하는 버스트 코드화(Burst Coding), 스파이크의 위상을 이용하는 위상 코드화(Phase Coding) 등 다양한 방식이 존재한다[38]. 이러한 코드화는 정보를 간단하게 표현하고 빠르게 처리하며, 대규모 병렬 계산을 가능하게 한다[39].
2. 스파이킹 신경망의 학습
뉴런 간 시냅스의 강도가 입력 스파이크와 출력 스파이크의 시간적 구성에 의해 결정된다는 사실은 스파이크 타이밍 의존 가소성(STDP: Spike-Timing-Dependent Plasticity)으로 알려져 있으며[40], 이는 Hebb의 법칙에 기반한 시냅스의 학습 원리로서 다양한 종에 대한 관찰을 통해 입증되었다. 입력 스파이크가 발생한 직후 출력 스파이크가 발생하면 시냅스의 연결 강도가 강화되는데 이를 장기 강화(Long-Term Potentiation)라 하고, 출력 스파이크가 발생한 직후 입력 스파이크가 발생하면 시냅스의 연결 강도가 약화되는데 이를 장기 억압(Long-Term Depression)이라 한다. 강화와 억압 모두 입력 스파이크와 출력 스파이크의 발생 간격이 가까울수록 연결 강도를 크게 더욱 크게 변화시킨다.
마찬가지로 스파이킹 신경망의 학습 과정은 스파이킹 뉴런 간의 시냅스의 연결 강도를 조정하는 과정을 의미한다. 가장 많이 알려진 학습 방법은 STDP를 그대로 활용하여 비지도 학습을 진행하는 것이다. 서로 연결된 스파이킹 뉴런들은 스파이크로 표현된 데이터 간의 시간적 구성을 학습하고, 데이터에 담긴 패턴을 표현할 수 있도록 학습된다[41]. 한편, 스파이킹 신경망을 위한 지도 학습 방법도 있다. 심층신경망의 역전파와 유사하게 스파이킹 신경망의 출력 스파이크열과 원하는 출력 스 파이크열의 차이를 반영하는 손실함수를 정의하고, 손실을 최소화하도록 학습하는 것이다. 잘 알려진 지도 학습 방법으로 SpikeProp이 있다[42].
3. 스파이킹 신경망의 전망
스파이킹 신경망의 스파이킹 뉴런은 모델 자체에 내포되어 있는 시간적 요소 덕분에 시간 정보가 포함된 데이터를 다루기 용이하고[43], 정보를 코드화하여 간단하게 표현할 수 있으며, 그 결과 시스템의 에너지 효율이 증가한다[28].
스파이킹 신경망이 생물학적 근사성을 바탕으로 인간의 두뇌가 가지는 적응력, 시공간적 처리 능력을 재현하여 심층신경망이 고전하고 있는 난제들을 해결할 수 있으리라는 기대 하에 많은 연구가 진행되고 있다. 또한 스파이킹 신경망의 동작을 분석하여 뇌의 인지 과정 메커니즘을 추정하고 검증하는 도구로 사용될 수도 있을 것이다.
Ⅳ. 브레인 네트워크
지금까지는 뉴런 네트워크의 관점에서 출발한 기계학습 방법들에 대해 살펴보았다. 반도체 소자들로부터 출발하여 휴대전화의 복잡한 기능을 이해하는 것이 어려운 것처럼, 미시적인 뉴런들을 결합하여 복잡한 뇌의 메커니즘을 이해하는 것은 상당히 난해한 일이다. 휴대전화의 기능을 구성 부품들의 역할과 이들을 상호작용으로 파악할 수 있듯이, 뇌 또한 유의미하게 구분되는 다수의 영역과 이들의 상호 네트워크로 이해할 수 있을 것이다. 이 장에서는 이러한 영역 네트워크 관점, 즉 메조스케일 또는 매크로스케일의 브레인 네트워크 분석(Brain Network Analysis)을 기반으로 뇌를 모사하는 기계학습 방법에 대해 소개하고자 한다.
1. 브레인 네트워크 모델
브레인 네트워크는 뇌를 해부학적 또는 기능적으로 영역화하여 각 영역을 노드(Node), 영역 간의 연결을 엣지(Edge)로 그래프화하여 표현한 것으로서, 이를 바탕으로 뇌에 대한 동역학(Dynamics), 제어(Control) 등의 연구가 이루어진다. 이러한 접근 방식은 뇌에 대한 범용적, 직관적인 표현을 가능하게 하고 인공신경망에 접목시키기 용이하다. 또한 네트워크 신경과학(Network Neuroscience)을 통한 네트워크 측면에서의 통합 연구도 가능하다[44].
브레인 네트워크의 노드와 엣지를 구성하기 위한 접근 방법은 해부학적인 모사와 기능적인 모사로 나눌 수 있다. 두 접근 방법 모두 DTI(Diffusion Tensor Imaging), EEG(Electroencephalogram) 등의 관측 자료를 바탕으로 뇌를 다수의 영역으로 나누고 각 영역을 노드로 정의한다. 엣지의 구성은 접근 방법에 따라 상이한데, 우선 해부학적 모사의 경우 주로 DTI를 통해 측정한 백질신경로의 수량, 밀도 등을 수치화하고[45], 이를 단위 영역에 포함된 전체 신경로에 대해 정규화한다. 엣지 구성을 위한 기능적 모사는 fMRI(functional Magnetic Resonance Imaging)를 통해 얻은 시계열 데이터를 활용하는데, 각 영역의 활성화 정도에 관한 시계열 데이터 간의 상관성을 피어슨 상관관계(Pearson Correlation), ICA(Independent Component Analysis) 등을 통해 엣지를 계량화한다[45].
브레인의 특성은 개체마다 상이할 수 있으므로 공통된 특성을 추출하여 모델을 구성해야 한다. 이를 위해 여러 개체로부터 추출한 다수의 브레인 네트워크 모델에 대해 그룹 임계화(Thresholding) 등의 통계적 처리를 거쳐 표본집단을 대표할 수 있는 컨센서스 네트워크(Consensus Network)를 구성하게 된다.
2. 레저버 컴퓨팅
가. 개요
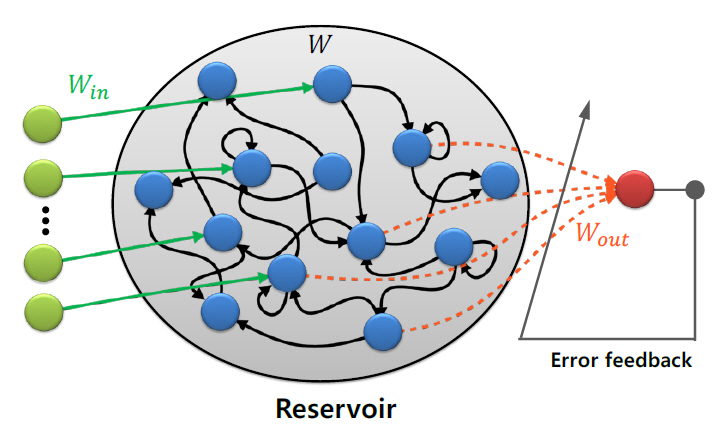
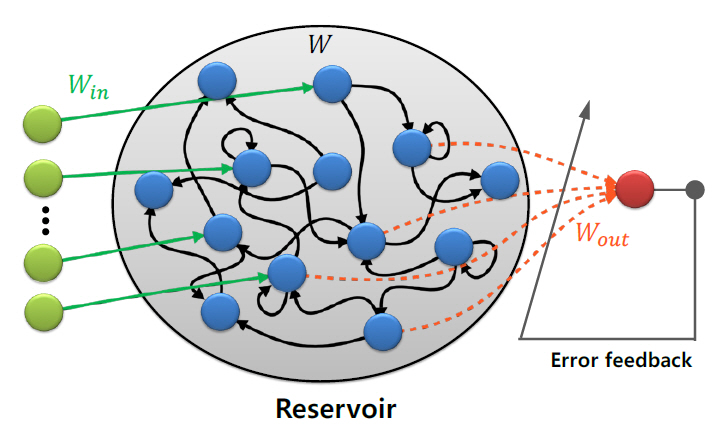
레저버 컴퓨팅(RC: Reservoir Computing)은 그림 4에 나타낸 바와 같이 고정된 네트워크(레저버)를 활용하여 정보를 처리하는 모델로서, RNN(Recurrent Neural Network)으로부터 파생되었다[46]. RC 모델은 고정된 네트워크인 레저버와 레저버의 출력을 입력으로 받는 분류기로 구성된다. 중요한 것은 레저버 부분의 가중치는 초기에 설정한 값으로 고정되고, 모든 학습이 레저버 출력단에 연결된 분류기에서 이루어진다는 것이다. 때문에 기존 RNN에 비해 훨씬 적은 컴퓨팅 자원으로 학습이 가능하다. 또한 더 나은 생물학적 근사성을 가지고 있어 뇌과학과의 시너지 효과를 기대할 수 있다.
나. ESN
RC는 기계학습 관점에서의 ESN(Echo State Network)과 뇌과학 관점에서의 LSM(Liquid State Machines)으로 제안되었다. 이중 ESN은 2001년 Herbert Jaeger가 제안한 개념으로서, 레저버가 특정 조건을 만족한다면 이를 고정한 채 그 출력만을 선형 분류기로 학습하는 것으로도 충분한 성능을 얻을 수 있을 것이라는 아이디어에서 착안한 모델이다. Jaeger는 이 조건을 ESP(Echo State Property)라 정의하였다.
ESP조건이 RC모델의 필요조건은 아니지만 유의미한 학습이 가능한 무작위 행렬을 만드는 수학적 기준으로 유용하게 사용된다[47]. 이후 ESP에 몇 가지 조건을 추가하여 더 복잡한 작업을 수행할 수 있는 가중치를 찾는 연구나 ESN이 보편적 근사가 가능한 모델(Universal Approximator)임을 증명하는 연구가 이루어졌다[48].
다. LSM
LSM은 뇌과학, 그 중에서도 계산신경과학(Computational Neuroscience) 관점에서 제안된 개념이다. 계산신경과학은 뇌를 뉴런 단위부터 수학적으로 모델링하여 뇌의 작동 방식을 파악하는 뇌과학의 한 분야이다. 기계학습 관점에서 제안된 ESN이 생물학적 근사성보다 성능에 치중했다면, LSM은 성능보다는 더 나은 생물학적 근사성을 유지하는 데 주안점을 두었고, 주로 SNN과 결합되어 활용된다[49].
3. 브레인과 레저버 컴퓨팅
가. 커넥톰
커넥톰은 뇌에 존재하는 모든 뉴런 간의 연결을 표현한 일종의 연결망 지도이다[50]. 하지만 뉴런 간의 연결은 수가 많을 뿐 아니라 개체별로 상이하고 동일 개체 내에서도 지속적으로 변화하기 때문에 완전한 커넥톰을 구성하기란 매우 어렵다. 2010년 인간 커넥톰 프로젝트가 시작되었지만, 인간의 뇌는 물론 쥐나 초파리의 커넥톰조차 아직 완전히 밝혀지지 않았다. 현재 완전히 밝혀진 커넥톰은 302개의 뉴런으로 이루어진 예쁜꼬마선충의 커넥톰뿐이다[51].
다행히 뇌 전체를 재현해야만 커넥톰을 활용할 수 있는 것은 아니다. 보통 뇌는 해부학적 혹은 기능적으로 영역화하여 다뤄지는데, 이미 많은 연구를 통해 뇌가 모듈성(Modularity) 및 작은 세상(Small World) 특성을 가진 다중스케일 기관이라고 밝혀졌기 때문에 효율적이고 현실적인 접근 방법이라 할 수 있다[50,52]. 최근 컴퓨터 성능과 뇌 이미지 측정 기술의 발전에 힘입어 일부 뇌 영역의 커넥톰 혹은 메조스케일 커넥톰이 속속 발표되고 있으며[53,54], 이를 활용한 다양한 연구가 진행 중이다[55,56].
나. 브레인 네트워크 기반 레저버 컴퓨팅
RC 모델 학습 과정에서 학습에 참여하지 않는 레저버는 일종의 사전 지식(Prior Knowledge) 역할을 한다. 이 사전지식은 일반적으로 ESN처럼 ESP라는 수학적 특성을 유도하여 얻거나, LSM처럼 반복적 탐색을 통해 얻는다. 하지만 이러한 방식을 통해 얻은 레저버 가중치는 실제 뇌의 정보를 기반으로 하지 않기 때문에 생물학적 근사성이 떨어진다고 볼 수 있다[55].
이를 해결하기 위해 뇌과학을 기반으로 구성된 양질의 브레인 네트워크를 직접 레저버로 사용하고자 하는 연구가 진행되고 있으며[55,56], 이들 연구에서는 컨센서스 네트워크를 인접행렬(Adjacency Matrix)로 표현하여 레저버 가중치로 사용한다. 이렇게 구성된 RC 모델의 기억 용량(Memory Capacity)을 테스트 해본 결과 브레인 네트워크로 구성한 가중치가 무작위 가중치보다 성능적으로 더 뛰어나면서도 낮은 연결 비용(Wiring Cost)을 가진다는 것이 확인되었다[55,56]. 이는 해당 방법론이 생물학적 근사성이 높고 성능이 준수한 모델을 학습할 수 있는 방법임을 시사한다.
Ⅴ. 브레인 네트워크의 유의미한 특성들
이 장에서는 브레인 모사 AI의 새로운 연구 방향을 모색하기 위해 아직 AI에 구체적으로 반영되지 않은 브레인 네트워크의 유의미한 특성들에 대해 소개하고자 한다.
1. 동시 진동
동시 진동(Synchronized Oscillation)은 다수의 뉴런이 동시 발생적인 활동을 통해 거시적인 진동을 만들어내는 현상으로서 뇌의 다양한 기능과 밀접하게 연관되어 있다[57]. 동시 진동의 결과로 나타나는 뇌파는 이미 19세기에 EEG를 이용하여 최초로 검출되었지만, 뇌파 현상의 생리학적, 병리학적, 인지 기능적 역할에 대한 연구는 관측 장비와 컴퓨터 기술에 발달에 힘입어 10여 년 전부터 비로소 본격적으로 진행되어왔다[58]. 동시 진동은 다양한 리듬의 뇌파를 발생시키는데, 최근에는 이러한 진동이 뉴런 그룹 간의 통신을 효과적이고, 정확하고, 분별적으로 이루어지도록 할 뿐 아니라, 기억을 형성하거나 검색하는 데에도 관여한다는 사실이 밝혀졌다[57,59].
다른 뉴런으로부터 신호를 받아들이고 변환하여 또 다른 뉴런에 전달하는 뉴런의 개별 활동이 어떻게 수많은 뉴런의 일사불란한 단체 활동을 야기하는지에 대해서는 아직 완전히 밝혀지지 않고 있지만, 이러한 동시 진동 현상은 인간 수준의 AI가 지녀야 할 창발적 특성 중 하나로 생각해 볼 수 있다.
2. 모티프
모티프(Motif)는 다수의 노드와 노드 사이의 연결로 이루어진 복잡 네트워크를 구성하는 기본 요소로서 네트워크에서 높은 확률로 관찰되는 특정한 연결 패턴을 의미한다[60]. 브레인 네트워크에 존재하는 모티프는 정보의 통합과 분별에 핵심적인 역할을 하는데[60], 뇌는 가능한 적은 수의 모티프를 유지하면서 각 모티프 내의 다양한 변화를 통해 효율적으로 정보를 처리한다는 것이 알려졌다[61]. 즉, 뇌는 구조적인 틀을 최대한 유지하면서 틀 내에서의 다양성을 극대화하는 방식으로 변화에 대응한다고 볼 수 있다.
이는 인공신경망 모델이 연속학습을 위해 새로운 학습을 시도할 때 이전의 학습 내용을 상실하는 파국적 망각 현상을 극복할 수 있는 실마리가 될 수 있다. 파국적 망각은 새로운 학습을 위해 인공신경망 모델에 변형을 가할 때 기존의 틀을 유지하는 장치 없이 새로운 정보가 모델의 구성 요소에 그대로 반영되기 때문이라고 볼 수 있는데, 브레인 네트워크가 가진 모티프의 성질을 이용한다면 공통된 지식을 유지하면서도 차이에 대해 유연하게 학습할 수 있는 모델을 고안할 수 있을 것이다.
3. 동적 재구성
브레인 네트워크의 영역을 노드로 표현할 때 특정한 기능을 수행하는 다수의 노드 집합을 모듈이라 정의하는데, 이른바 “학습” 현상을 모듈의 동적 재구성(Dynamic Reconfiguration)을 통한 적응적 변화로 이해할 수 있다[62]. 최근의 연구 결과[63]에 따르면 특정 영역이 소속된 모듈을 빈번하게 바꾸는 동적 재구성 과정을 통해 작업 기억, 계획, 추론 등과 같은 고차원적인 두뇌 활동이 이루어진다고 한다.
이는 AI 모델이 현재 달성하고 있는 패턴 인식(Pattern Recognition) 수준을 넘어 고차원적인 인지기능(Cognition)를 갖추기 위해서는 독립적인 기능을 가진 모듈이 존재하면서도 학습을 위해 모듈 간의 유연한 변화가 가능한 특성을 가져야 한다는 것을 암시한다.
4. 생성 모델
브레인 네트워크의 생성 모델(Generative Model)은 특정 규칙에 의해 생성된 합성 네트워크로서 실제 뇌가 가진 여러 가지 특성들을 그대로 재현하는 것을 목표로 한다[64]. 생성 모델이 뇌를 성공적으로 모사한다면 생성 규칙을 이용하여 데이터로서 관찰되지 않은 뇌의 특성까지도 예측할 수 있을 것이다. 더 나아가 생성 규칙의 고찰을 통해 브레인 네트워크의 메커니즘을 밝힐 수 있을 것으로 기대되어 최근 활발한 연구가 진행되고 있다.
생성 모델의 연구의 최종 목표는 우리가 추구하는 브레인 모사 기계학습 연구의 최종 목표와 맞닿아 있다. 뇌를 정확하게 모사할 수 있는 합성 네트워크는 곧 뇌의 기능을 갖춘 AI를 의미하기 때문이다.
Ⅵ. 결론
뇌과학은 오랜 시간 동안 AI 연구 개발에 지속적인 영감을 부여하며 지대한 영향을 미쳐왔다. 뉴런에 대한 Hebb의 학습으로부터 영감을 받은 인공신경망 모델은 심층신경망 기반의 다양한 시스템으로 발전하여 이미지, 영상, 언어, 음성 등 폭넓은 분야에서 그 유용성을 증명했지만, 그와 동시에 여러 가지 한계를 드러내기도 했다. 이러한 한계를 근본적으로 해결하기 위해 다시 뇌과학으로부터 실마리를 구하려는 시도가 활발히 진행되고 있으며, 생물학적 근사성을 반영한 DNN, SNN, 커넥톰 기반의 네트워크 등이 그 예이다. 최근 뇌과학의 비약적인 발달로 인해 뇌의 메커니즘이 하나씩 그 모습을 드러내고 있으며, 특히 브레인 네트워크 분야에서는 현재 AI가 제대로 구현하지 못하고 있는 인간의 인지 기능에 대한 작동 원리가 구체적으로 밝혀지고 있다. AI 모델이 뇌의 원리를 보다 정확하게 모사한다면 궁극적 목표인 인간 수준의 AI(Human-Level AI)에 도달할 수 있을 것이다.
약어 정리
AI
Artificial Intelligence
CNN
Convolutional Neural Network
DNN
Deep Neural Network
DTI
Diffusion Tensor Imaging
EEG
Electroencephalogram
ESN
Echo State Network
ESP
Echo State Property
fMRI
functional Magnetic Resonance Imaging
ICA
Independent Component Analysis
LSM
Liquid State Machine
LSTM
Long Short-Term Memory
QNN
Quantized Neural Network
RC
Reservoir Computing
RL
Reinforcement Learning
RNN
Recurrent Neural Network
D. Hassabis et al., "Neuroscience-inspired artificial intelligence," Neuron, vol. 95, no. 2, July 2017, pp. 245-258.
N.C. Thompson et al., "The computational limits of deep learning," July 2020, arXiv: 2007.05558.
M.M. Waldrop, "What are the limits of deep learning?," PNAS, vol. 116, no. 4, Jan. 2019, pp. 1074-1077.
D. Heaven, "Deep trouble for deep learning," Nature, vol. 574, no. 7777, Oct. 2019, pp. 163-166.
Wikimedia Commons: Components of neuron, https://commons.wikimedia.org/wiki/File:Components_of_neuron.jpg.
Wikimedia Commons: Connectome extraction procedure, https://commons.wikimedia.org/wiki/File:Connectome_extraction_procedure.jpg.
Wikimedia Commons: The Human Connectome, https://commons.wikimedia.org/wiki/File:The_Human_Connectome.png.
K. Lucas, "The ‘all or none’ contraction of the amphibian skeletal muscle fibre," J. Physiol., vol. 38, no. 2–3, 1909, pp. 113–133.
W.S. Mcculloch et al., "A logical calculus of the ideas immanent in nervous activity," Bull. Math. Biophys, vol. 5, no. 4, 1943, pp. 115-133.
D.O. Hebb, The organization of behavior: A neuropsychological theory, Psychology Press, London, UK, 2005.
E.L. Bienenstock et al., "Theory for the development of neuron selectivity: Orientation specificity and binocular interaction in visual cortex", J. Neurosci., vol. 2, no. 1, 1982, pp. 32-48.
E. Oja, "Simplified neuron model as a principal component analyzer," J. Math. Biol., vol. 15, no. 3, 1982, pp. 267-273.
F. Rosenblatt, "The perceptron: A probabilistic model for information storage and organization in the brain," Psychol. Rev., vol. 65, no. 6, 1958, pp. 386-408.
F. Rosenblatt, "Principles of neurodynamics. Perceptrons and the theory of brain mechanisms," Cornell Aeronautical Lab, Buffalo NY, USA, 1961.
M. Minsky and S.A. Papert, Perceptrons: An introduction to computational geometry, MIT press, London, UK, 2017.
J.J. Hopfield, "Neural networks and physical systems with emergent collective computational abilities," PNAS, vol. 79, no. 8, 1982, pp. 2554-2558.
G.E. Hinton and T.J. Sejnowski, "Learning and relearning in Boltzmann machines," Parallel Distrib. Process.: Explor. Microstruct. Cogn., vol. 2, no. 1, 1986, pp. 282-317.
G.E. Hinton, S. Osindero, and Y.W. Teh, "A fast learning algorithm for deep belief nets," Neural Comput., vol. 18, no. 7, July 2006, pp. 1527–1554.
R.M. French, "Catastrophic forgetting in connectionist networks," Trends Cogn. Sci., vol. 3, no. 4, 1999, pp. 128-135.
T. Hospedales et al., "Meta-learning in neural networks: a survey," Nov. 2020, arXiv: 2004.05439.
S. Hochreiter et al., "Long short-term memory," Neural Comput., vol. 9, no. 8, 1997, pp. 1735-1780.
T.P. Lillicrap et al., "Backpropagation and the brain," Nat. Rev. Neurosci., vol. 21, Apr. 2020, pp. 335–346.
T.P. Lillicrap et al., "Random synaptic feedback weights support error backpropagation for deep learning," Nat. Commun., vol. 7, no. 1, Dec. 2016, pp. 1-10.
Y. Bengio et al., "Towards biologically plausible deep learning," Aug. 2016, arXiv: 1502.04156.
J.C.R. Whittington et al., "Theories of error back-propagation in the brain," Trends Cogn. Sci., vol. 23, no. 3, Mar. 2019, pp. 235–250.
A. Tavanaei et al., "Deep learning in spiking neural networks," Neural Netw., vol. 111, Mar. 2019, pp. 47–63.
W. Xiao et al., "Biologically-plausible learning algorithms can scale to large datasets," Dec. 2018, arXiv: 1811.03567.
C. Baldassi et al., "Learning may need only a few bits of synaptic precision," Phys. Rev. E, vol. 93, no. 5, May 2016.
W. Wen et al., "TernGrad: Ternary gradients to reduce communication in distributed deep learning," Dec. 2017, arXiv: 1705.07878.
M. Rastegari et al., "XNoR-Net: ImageNet classification using binary convolutional neural networks," in Computer Vision–ECCV 2016, vol. 9908, Springer, Cham Switzerland, 2016, pp. 525–542.
Y. Yang et al., "Training high-performance and large-scale deep neural networks with full 8-bit integers," Neural Netw., vol. 125, May 2020, pp. 70–82.
M. Lechner et al., "Neural circuit policies enabling auditable autonomy," Nat. Mach. Intell., vol. 2, Oct. 2020, pp. 642-652.
E.D. Adrian et al., "The impulses produced by sensory nerve endings," J. Physiol., vol. 61 no. 4, 1926, pp. 465-483.
G.Q. Bi et al., "Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type," J. Neurosci., vol. 18, no. 24, 1998, pp. 10464-10472.
W. Guo et al., "Neural coding in spiking neural networks: A comparative study for robust neuromorphic systems," Front. Behav. Neurosci., vol. 15, 2021.
S.J. Thorpe, "Spike arrival times: A highly efficient coding scheme for neural networks," Parallel Process. Neural Syst., 1990, pp. 91-94.
D.E. Feldman, "The spike-timing dependence of plasticity," Neuron, vol. 75, no. 4, 2012, pp. 556-571.
T. Masquelier et al., "Spike timing dependent plasticity finds the start of repeating patterns in continuous spike trains," PloS one, vol. 3, no. 1, 2008, e1377.
S.M. Bohte et al., "SpikeProp: Backpropagation for networks of spiking neurons," in Proc. ESANN, Bruges, Belgium, Apr. 2000, pp. 419-424.
A. Kugele et al., "Efficient processing of spatio-temporal data streams with spiking neural networks," Front. Neurosci., vol. 14, 2020.
A. Fomito and E.T. Bullmore, "Connectomic intermediate phenotypes for psychiatric disorders," Front. Psychiatry, Apr. 2012.
M. Lukosevicius, H. Jaeger, and B. Schrauwen, "Reservoir Comput. Trends," vol. 26, May 2012, pp. 365–371.
H. Jaeger, "The "echo state" approach to analysing and training recurrent neural networks–with an erratum note," Bonn, GMD Tech. Rep. vol. 148, Jan. 2010.
L. Grigoryeva et al., "Echo state networks are universal," Neural Netw., vol. 108, Dec. 2018, pp. 495-508.
H. Jaeger, W. Maass, and J. Principe, "Special issue on echo state networks and liquid state machines," Neural Netw., vol. 20, no. 3, Apr. 2017, pp. 287-289.
O. Sporns, "The human connectome: Origins and challenges," NeuroImage, vol. 80, Oct. 2013. pp. 53-61.
S.W. Oh et al., "A mesoscale connectome of the mouse brain," Nature, vol. 508, no. 7495, Apr. 2014.
D. Meunier et al., "Hierarchical modularity in human brain functional networks," Front. Neuroinform., vol. 3, 2009.
N.T. Markov et al., "A weighted and directed interareal connectivity matrix for macaque cerebral cortex," Cereb. Cortex, vol. 24, 2014.
R.F. Betzel and D.S. Bassett, "Specificity and robustness of long-distance connections in weighted, interareal connectomes," PNAS, vol. 115, no. 2, May 2018.
L.E. Suarez et al., "Learning function from structure in neuromorphic networks," Preprint form Biology, Nov. 2020, doi: 10.1101/2020.11.10.350876.
W. Luo and Ji-Song Guan, "Do brain oscillations orchestrate memory?," Brain Sci. Adv., vol. 4, no. 1, Oct. 2018. pp. 16-33.
R. Fuevara Erra et al., "Neural synchronization from the perspective of non-linear dynamics," Front. Comput. Neurosci., Oct. 2017.
P. Fries, "Rhythms for cognition: Communication through coherence," Neuron, vol. 88, no. 1, Oct. 2015.
C. Duclos et al., "Brain network motifs are markers of loss and recovery of consciousness," Sci. Rep., vol. 11, Mar. 2020.
D.S. Bassert et al., "Dynamic reconfiguration of human brain networks during learning," PNAS, May 2011, pp. 7641-7646.
M. Pedersenet al., "Multilayer network switching rate predicts brain performance," PNAS, vol. 115, Dec. 2018.
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.