시계열 데이터 결측치 처리 기술 동향
Technical Trends of Time-Series Data Imputation
- 저자
-
김에덴에너지지능화연구실 kimed93@etri.re.kr 고석갑에너지지능화연구실 softgear@etri.re.kr 손승철에너지지능화연구실 sson@etri.re.kr 이병탁에너지지능화연구실 bytelee@etri.re.kr
- 권호
- 36권 4호 (통권 191)
- 논문구분
- 일반논문
- 페이지
- 145-153
- 발행일자
- 2021.08.01
- DOI
- 10.22648/ETRI.2021.J.360414
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- Data imputation is a crucial issue in data analysis because quality data are highly correlated with the performance of AI models. Particularly, it is difficult to collect quality time-series data for uncertain situations (for example, electricity blackout, delays for network conditions). Thus, it is necessary to research effective methods of time-series data imputation. Many studies on time-series data imputation can be divided into 5 parts, including statistical based, matrix-based, regression-based, deep learning (RNN and GAN) based methodologies. This study reviews and organizes these methodologies. Recently, deep learning-based imputation methods are developed and show excellent performance. However, it is associated to some computational problems that make it difficult to use in real-time system. Thus, the direction of future work is to develop low computational but high-performance imputation methods for application in the real field.
Share
Ⅰ. 서론
4차 산업혁명 시대를 지나며 ICT 응용 분야는 많은 발전을 하고 있다. 특히 인공지능(AI: Artificial Intelligence) 분야는 핵심 기술로 여러 영역에 실제로 적용되기 위해 다양한 연구가 진행되고 있다. 기본적으로 인공지능 기술을 접목하기 위해서는 기술에 기반이 되는 양질의 데이터가 필요하다. 이는 인공지능 기술의 성능 향상에 영향을 주기 때문에 매우 중요한 문제이다. 그 중, 산업 현장에 자주 사용되는 시계열 데이터는 시간 동기화에 맞추어 오랜 시간 수집되어야 의미가 있는 데이터로서 인공지능 기술에 쓰일 수 있다. 하지만, 현실에서는 예상치 못한 상황들(예, 정전, 통신장애 등)의 발생으로 인한 정보 누락이 발생하여 분석에 적절하지 못한 경우가 많다. 때로는 수집된 데이터의 절반 이상이 누락되어 있는 경우도 존재한다. 이러한 데이터를 그대로 인공지능 기술에 적용하기에는 무리가 있고, 기존 데이터를 버리고 다시 수집하기에는 많은 시간 소요와 정전 등 예상치 못한 상황이 발생하지 않을 것이라는 보장도 없다. 따라서 이와 같은 문제의 해결 방안으로는 수집을 다시 하기보다는 기존 수집된 데이터의 결측값을 대치하여 사용하는 것이다. 이를 위해, 정확한 결측값 대치 및 처리 방법에 관한 다양한 연구가 진행되었고, 본고에서는 결측치 종류 및 결측치 처리 기술 연구 동향을 소개하고자 한다.
본고의 구성은 다음과 같다. Ⅱ장에서는 결측치 데이터의 종류에 대하여 정의하고, Ⅲ장에서는 결측치 처리에 관한 연구 동향을 통계적 기법, 행렬기반 기법, 회귀분석 기법, RNN(Recurrent Neural Network) 기반 기법, GAN(Generative Adversarial Network) 기반 기법과 같이 크게 다섯 분류로 나누어 소개한다. 마지막 Ⅳ장 결론에서는 연구 동향에 맞추어 앞으로의 결측치 처리 기법에 관한 시사점을 제시하고 마무리한다.
Ⅱ. 결측치 데이터 종류
1. 완전 무작위 결측(MCAR)
결측값의 첫 번째 종류는 완전 무작위 결측(MCAR: Missing Completely At Random)이다. MCAR은 전체에 걸쳐 무작위하게 누락된 경우로 변수의 종류, 변수의 값과 상관없이 비슷한 분포로 누락된 데이터를 의미한다. 이 경우 통계적으로 누락 패턴을 파악해 볼 수 있다. 이러한 형태의 결측치는 분석에 크게 영향을 주지 않지만 실제로 MCAR인 경우는 거의 없다.
2. 무작위 결측(MAR)
무작위 결측(MAR: Missing At Random)은 어떤 특정 변수에 대하여 데이터가 누락되는 경우를 의미하며, 결측값의 경우가 자료 내의 다른 변수와 관련이 있다. 다만, 그 변수의 값과는 관계가 없다. 예를 들어, 설문 대상자가 뒷면이 있는지 모르고 설문을 진행하여 특정 변수들에 국한되어 누락된 경우가 해당한다.
3. 비무작위 결측(MNAR)
비무작위 결측(MNAR: Missing Not At Random)의 경우는 누락되는 부분들이 무작위로 누락되는 것이 아닌 누락된 변수의 값이 누락된 이유와 관련이 있는 경우이다. 대부분의 결측 데이터는 MNAR인 경우가 많다. 예를 들어, 시계열 데이터의 경우 측정 센서의 고장이나 네트워크 통신 문제 등으로 누락되는 경우는 변수의 값이 누락된 이유와 관련 있기 때문에 MNAR에 해당한다.
결측치 데이터 종류 중에서 (1) MCAR와 (2) MAR의 경우는 무작위로 누락되어 있는 경우이기 때문에 결측값을 제거한 데이터를 이용하여 분석을 진행하는 것이 좋다. 반면, (3) MNAR의 경우는 결측값의 발생이 무분별하기 때문에 결측값이 있는 데이터를 제거하고 분석을 진행할 경우, 모델이 편향적으로 학습될 수 있기 때문에 일반화된 모델을 설계하는 것에 어려움이 존재한다. 따라서 이의 경우에는 단순한 결측치 제거가 아닌 상황에 맞는 결측치 보간 및 처리 방법이 매우 중요하다.
Ⅲ. 시계열 데이터 결측치 처리 동향
1. 통계적 기법
결측치 처리의 가장 간단한 방법으로는 결측 데이터를 제거하는 방법이 있었지만, Ⅱ장에서 살펴본 바와 같이 MNAR의 경우 효과적이지 않아 결측값 대치 방법에 관하여 다양한 연구가 진행되었다. 그 중 통계적인 기법을 통한 결측치 처리는 가장 기초적인 방법이다.
통계적 기법 중에서도 쉬운 방법으로는 결측치 앞뒤 값에 대한 평균, 중앙값 등 기초 통곗값을 채워 넣는 단순 대입법이 있다[1]. 이와 같은 대입법은 보통 라이브러리 패키지로 제공된다. 파이썬에서는 사이킷런 라이브러리[2]에서 제공하고 있고, R에서는 ImputeTS[3] 패키지가 다음과 같은 기능들을 포함하여 제공하고 있다. 단순 대입법은 간단하고 시간의 소요가 적지만 일편적인 방법이기 때문에 표준 오차가 과소 추정되는 단점이 존재한다[4]. 이를 보완하기 위해 확률 대치 방법으로 Hotdeck 방법[5] 또는 Nearest-Neighbor 방법[6] 등이 제안되었지만, 대부분은 추정량의 표준 오차 계산 자체가 어려운 경우가 많다는 단점이 존재한다.
이와 같은 단일변량 신호에 대한 결측치 처리 기법보다 발전된 형태로 다변량 변수에도 적용 가능한 다중 대치법(MI: Multiple Imputation)에 관한 연구가 진행되었는데, 통계적 방법으로는 MICE (Multiple Imputation using Chained Equations)[7]가 자주 사용되는 방법으로 소개되었다. MICE는 결측치를 처리하는 데 각 복원 모델에 따라 대치를 진행하는 실용적인 방법이다. MICE는 완전 조건부 스펙과 순차 회귀 다변량 대치로도 알려져 있다. 모든 결측값은 처음에는 단순 무작위 샘플링 방법으로 채워진다. 결측값이 있는 첫 변수 x1은 다른 모든 변수 x2, ..., xk 에 의해 대하여 회귀된다. x1변수의 결측값은 x1의 해당 사후 예측 분포에서 시뮬레이션된 값으로 대체된다. 다음과 같이 다음 변수 x2는 x2를 제외한 다른 모든 변수에 대해 회귀되고 결측값은 사후 분포에서 추출된 값으로 대체되는 것으로 연쇄적인 특징을 가진다. 이러한 주기는 안정적인 결과를 얻기까지 일반적으로 결측값의 개수만큼 반복하여 이루어진다.
2. 행렬 기반 기법
결측치 처리를 위한 행렬 기반 기법들도 소개되었다. 행렬 분해(MF: Matrix Factorization) 방법은 행렬을 분해 및 재구성함으로써 데이터 간 상관관계를 도출하여 결측값을 대치하는 방법이다[8]. 기본적으로 MF 기반 접근법은 원본 데이터에서 특징 추출을 진행할 때 데이터의 행렬을 2개의 저차원 행렬로 분해한다. 그 후 원래 행렬을 재구성하는 시도를 거치면서 누락된 값을 대치하는 형태로 이루어진다. 기존 MF 기반 접근법은 시계열 데이터 결측값 대치에는 거의 사용되지 않았으나 최근 시계열 데이터에 적용 가능한 방법이 소개되었다.
TRMF(Temperal Regularized Matrix Factorization)[9]는 데이터 기반 시간 학습 및 예측하는 시간 정규화된 행렬 분해 프레임워크이다. 이는 결측값이 있는 고차원 시계열 데이터에 매우 적합하고 확장 가능한 행렬 분해를 사용한다. 시간적 종속성을 모델링할 뿐만 아니라 데이터 기반 종속성 특징도 학습하여 우수한 결과를 도출하였다.
다음은 관측된 시계열 데이터를 행렬로 변환하고 행렬 추정을 이용하여 결측치를 추정하고 미래값을 예측하는 방법이다[10]. 이는 모델에 구애받지 않으며 행렬 추정을 통하여 결측값을 대치한다.
PSMF(Probabilistic Sequential Matrix Factorization) [11]는 고차원 시계열로 구성된 시변량 및 비정상성 데이터 세트를 분해하기 위한 방법이다. 특히, 순차 근사 추론 결과를 통해 데이터 행렬을 분해하고 Markovian 종속성이 있어 그 구조를 이용하여 시간 종속성에 대한 속성을 저차원 특징 공간으로 인코딩할 수 있다. 또한, 칼만 필터 기법을 통하여 효율적으로 구성하였다. 따라서 PSMF는 일반적인 미분 가능한 비선형 부분적 공간 모델을 보정하고 추정하는 결측치 처리 방법이다.
3. 회귀분석 기법
회귀분석 기법은 과거의 데이터를 통하여 모델을 학습하여 예측하는 방법이다. 가장 간단한 방법으로는 선형 회귀분석이 있다[12]. 선형 회귀분석은 아주 단순한 모델이기 때문에 빠르고 간단하게 처리할 수 있으나, 전체적인 시계열 특성을 반영하지 못하고 앞뒤 순간만을 보고 판단하는 경우가 대부분이기 때문에 전체적인 데이터 흐름을 고려하지 못한다는 단점이 존재한다. 이러한 부분을 해소하기 위해 도입된 것이 시계열 모형이다. 대표적으로는 자기회귀모형(AR: Autoregressive)[13]이 존재한다. 대부분은 이 기본 모형의 개량 혹은 변형된 모형들로 사용된다. 이 중에서 기본적으로 가장 잘 알려진 모형은 ARIMA(Autoregressive Integrated Moving Average)모형으로 과거 데이터와 그의 추세를 반영하여 나타낼 수 있는 모형이다.
최근, AR 모형을 발전시킨 LATC(Low-Rank AutoRegressive Tensor Completion)[14] 모델이 소개되었다. 본 기술은 다변량 시계열 데이터를 3차원의 텐서 형태로 변환하여 AR 모델을 적용하는 것으로 텐서 형태로 변환할 때, 시간, 계절성, 다변량 변수 다음과 같은 3가지의 기준으로 고려한다. 기존의 단순한 AR 모델과 달리 데이터의 변환과 다변량 처리 기법을 통하여 결측값을 처리하는 것으로 기존보다 높은 성능을 보인다.
4. RNN 기반 기법
최근 발표된 딥러닝 기반 결측치 처리 방법 중에는 순환 신경망을 이용하는 사례가 아주 많다. 순환 신경망은 자연어, 음성 신호 등과 같이 시간의 흐름을 가지는 데이터의 시간 관계를 도출하기 위해 만들어진 알고리즘이다. 시계열 예측 등에 자주 사용되는데 이와 비슷한 결측치 처리 상황에도 적용된다. 특히 다변량 변수를 이용한 결측치 대치에 많이 사용되고, 최근에는 불규칙한 시계열 데이터의 결측 상황에도 적용 가능한 방법들에 대한 연구가 진행되었다.
M-RNN[15]은 Multi-directional Recurrent Neural Network의 약자로 새로운 딥러닝 아키텍처를 기반한 접근 방식이다. 보통의 데이터 처리의 경우 데이터 스트림 내의 보간 혹은 데이터 스트림을 패턴의 특성에 관한 가정을 통해 추정하는 경우이다. 이 논문에서 제안하는 M-RNN은 데이터 스트림 내에서 보간과 데이터 스트림에 대치하는 두 방법을 접목하여 제안하는 방식으로 소개된다. 특히 데이터 스트림의 관계가 중요한 의료 데이터에 관하여 통계적 보간법, MICE, 기본 RNN 기법 등과 비교하여 향상된 기능을 보여준다.
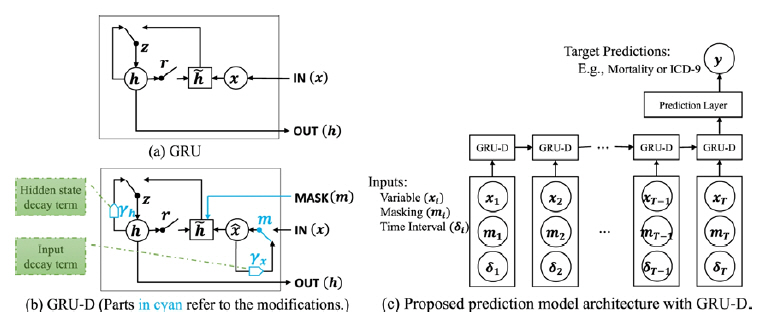
GRU-D[16]는 RNN기반의 결측치 처리를 위해 개발된 새로운 딥러닝 모델로 그림 1에서 구조를 확인할 수 있다. GRU-D는 순환 신경망의 GRU (Gated Recurrent Unit)를 기반으로 설계되었다. 기존 GRU모델에서 결측 여부를 보여주는 마스킹 정보와 결측된 시간 간격을 고려하여 이를 기존 모델 아키텍처에 감쇠율을 추가하여 효과적으로 적용하였다. 감쇠율은 다른 실제 값들이 시간 간격 정보에 따라 결측치에 대하여 영향을 얼마나 미치는지에 대한 모델링을 통해 결정된다. 이와 같은 새로운 방법을 통해 시계열의 장기적인 시간 종속성을 파악할 뿐만 아니라 누락된 패턴을 고려하여 더 나은 결측치에 대한 예측을 진행할 수 있다.
그림 1
(a) GRU의 구조, (b) GRU-D의 구조, (c) GRU-D의 전체 모델 아키텍처[16]
출처 Z. Che et al., “Recurrent neural networks for multivariate time series with missing values,” Scientific Reports, vol. 8, no. 1, 2018, pp. 1-12, CC BY 4.0,
BRITS(Bidirectional Recurrent Imputation for Time Series)[17]는 시계열 데이터에서 결측값 대치에 대하여 반복 신경망을 기본으로 하는 새롭게 제안된 모델이다. BRITS는 특정 분포의 가정 없이 결측값을 대치하기 위하여 동적 시스템을 양방향 RNN으로 조정한다. 이 방법은 여러 개의 상관된 결측값 처리가 가능하고, 비선형 역학을 기본으로 하는 시계열로 일반화가 가능하다. 또한, 데이터 기반 대치를 제공하며 누락 데이터가 있는 일반 상황에 적용 가능하다.
SSIM(Sequence-to-Sequence Imputation Model) [18]은 무선 센서 네트워크 상황에서 누락된 데이터를 복구하기 위한 새롭게 제안된 모델이다. SSIM은 최신 기술 중 하나인 Sequence-to-Sequence 딥러닝 아키텍처를 사용하며 과거와 미래의 정보를 모두 활용할 수 있도록 장단기 메모리 네트워크를 사용한다. 또한, 슬라이딩 윈도우 알고리즘으로 데이터양에 비해 많은 수의 훈련 샘플을 생성하기 때문에 적은 데이터 셋으로도 사용 가능한 알고리즘이다. 수질 모니터링 네트워크의 실제 시계열 데이터를 이용하여 MICE, ARIMA, Seasonal ARIMA 등의 대치 방법과 비교하여 더 우수한 성능을 보인다.
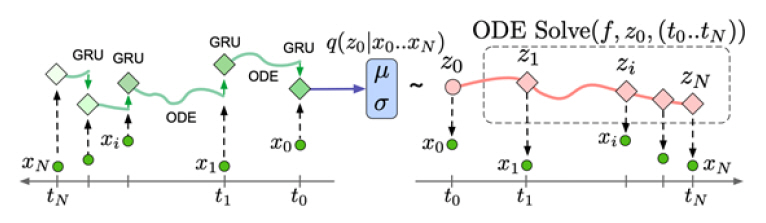
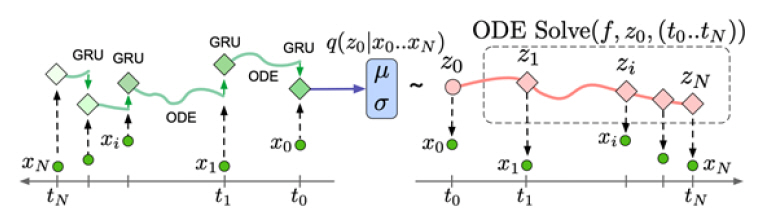
ODE-RNN[19]은 간격이 균일하지 않는 시계열 데이터에 대하여 단순한 RNN계열의 모델이 적용되기 어려운 점을 보완한다. ODE-RNN은 상미분 방정식(ODE: Ordinary Differential Equation)에 의해 RNN의 은닉 계수의 관계를 도출하여 학습하는 모델이다. 또한, 이어서 제안된 Latent ODE 모델 네트워크는 그림 2와 같은 구조를 가진다. 이러한 구조는 ODE-RNN과 달리 VAE(Variational AutoEncoder)를 기반으로 하여 ODE-RNN을 인코더 구조로 ODE를 디코더 구조로 이용하여 처리하는 방법으로 불규칙적으로 샘플링된 데이터도 ODE-RNN과 Latent ODE는 적용 가능하며 클래식 RNN 기반 모델보다 뛰어난 성능을 보여준다.
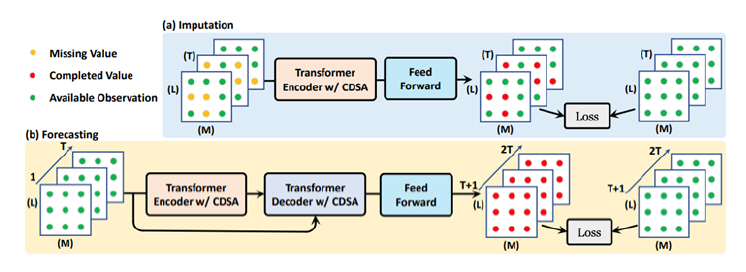
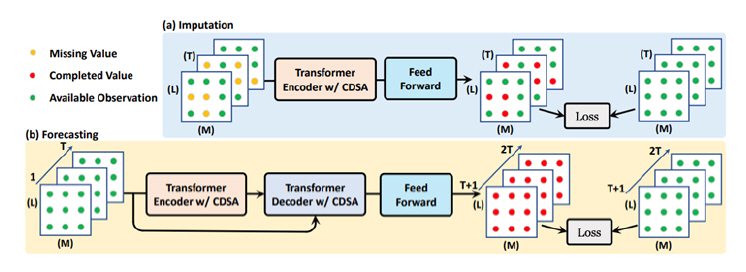
CDSA(Cross-Dimensional Self-Attention)[20]는 다변량의 지리적인 위치가 지정된 시계열 데이터 처리의 경우 적합한 모델이다. 그림 3은 CDSA 프레임워크를 보여준다. 이 모델은 다변량, 지리적 위치가 지정된 시계열 데이터(예, 대기질 데이터)에 대하여 Self Attention 아키텍처를 채택하였다. 이는 낮은 계산 복잡성을 유지하면서 시간, 위치 및 센서 측정을 포함한 여러 차원으로 Attention을 캡처하여 순차적으로 처리한다. 이 모델은 특히나 위치의 정보가 결합된 시계열의 데이터의 경우 더 효과적인 결측값 대치 혹은 예측 성능을 보인다.
5. GAN 기반 기법
RNN기반 결측치 처리 기법 이외에도, 최근에 발표된 논문 중에는 GAN을 이용하여 결측치를 처리하는 방법들이 연구되었다. GAN의 기본적인 원리는 입력 데이터의 확률적 분포를 알아내고 학습하여 데이터를 생성하는 것이 목적이다. 여기서 생성자(G)와 구분자(D)의 개념이 나오는데, 생성자(G)는 실제 데이터와 비슷한 데이터를 만들어 낼 수 있도록 학습을 진행하고, 구분자(D)는 실제 데이터와 생성자(G)가 생성한 가짜 데이터를 잘 구분할 수 있도록 설계된다. 이때 생성자(G)와 구분자(D)가 서로 대립하면서 성능을 개선하는 원리이다.
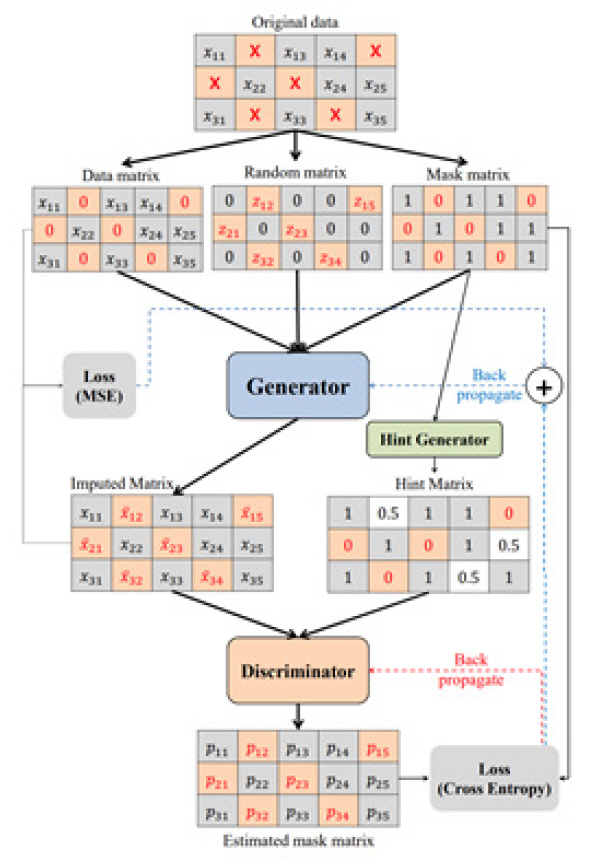
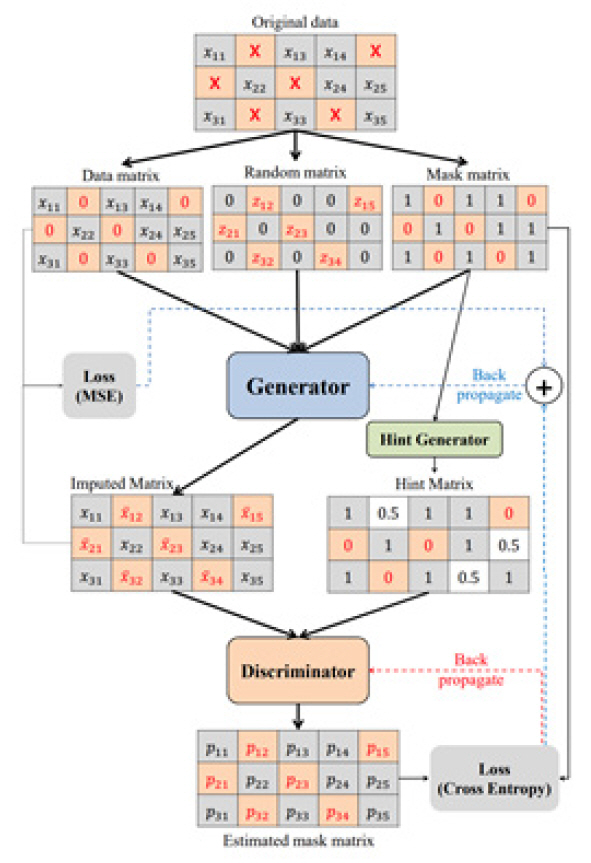
시계열 결측치 처리를 위해서도 이와 같은 GAN 알고리즘이 사용되었다. 가장 먼저 쓰인 알고리즘은 GAIN(Generative Adversarial Imputation Networks) [21]으로 구조는 그림 4와 같다. 생성자는 실제 데이터의 일부 구성요소를 관찰하고 실제로 관찰된 데이터에 따라서 결측된 데이터를 대치한다. 반면, 구분자는 대치된 데이터와 실제 데이터가 맞는지 판별한다. 이때 구분자(D)에 벡터 형식으로 몇 가지 원본 샘플 데이터의 누락에 대한 부분 힌트정보를 제공하고, 이 정보를 통해 G는 실제 데이터 분포에 따라서 생성하는 법을 학습하도록 한다.
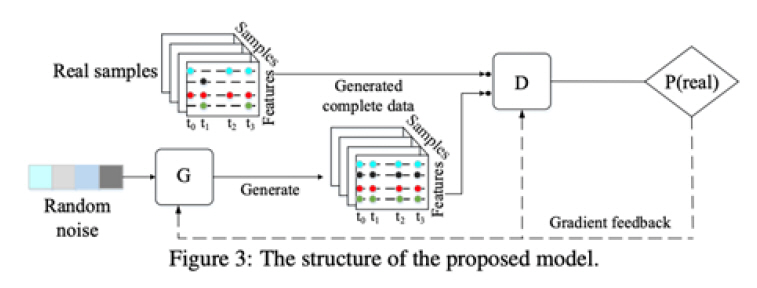
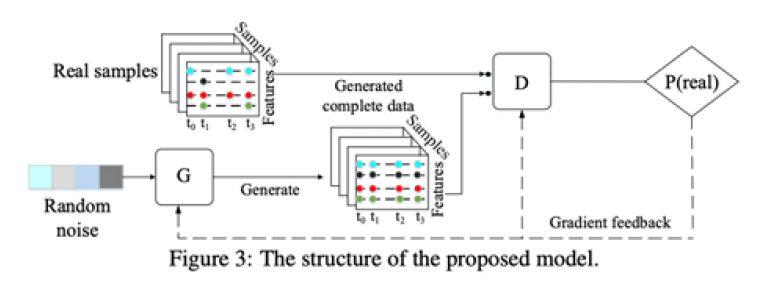
GRUI-GAN[22]은 기존에 RNN기반 딥러닝 기반 결측치 처리 방법 중 제안된 GRU-D 구조를 약간 변형하여 GAN의 구조에 결합한 기술이다. 그림 1에 나온 GRU-D의 구조에서 입력 부분의 감쇠를 제거한 GRU-I 구조를 사용하여 생성자(G), 구분자(D)를 구성한다. 전체 모델 아키텍처는 그림 5와 같다. GRU-I 구조는 큰 차이를 보이지 않지만 GAN의 구조의 결합함을 통해 적대적 구조를 이용하여 정확성은 높일 수 있는 모델이다. 하지만, 모델을 학습하는 데 많은 시간이 소요되며 임의의 노이즈가 입력으로 들어가기에 정확도가 안정적이지 못한 것으로 보일 수 있어 실용적이지 못하다는 단점이 존재한다.
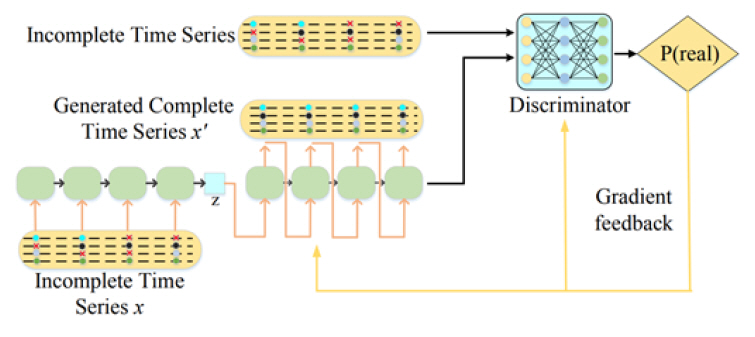
E2GAN[23]은 End-to-End 개념을 도입한 것으로 위의 GRUI-GAN을 개발한 연구진이 이어 최신 기술로 제안한 방법이다. 기존 제안된 GRUIGAN 모델은 임의의 노이즈 벡터를 사용하였지만, E2GAN은 생성기(G)에 GRUI를 기반한 오토 인코더 구조를 채택하여 구성하여 제안되었다. GRUI에 관한 개념은 크게 개선되지는 않고 기존의 마스크, 시간 지연, 감쇠율 등을 이용하여 진행되어 이 모델의 주된 기여는 오토 인코더 구조의 추가로 볼 수 있다. 그림 6에서 보여주는 것처럼 불완전한 시계열 데이터 x가 입력으로 들어가면 오토 인코더를 통해 저차원 벡터 Z로 압축한다.
NAOMI(Non-Autoregressive Multiresolution Sequence Imputation)[24]는 앞에 소개된 양방향 RNN을 갖춘 BRITS와 유사하게 이전 값과 미래 값 모두를 활용한 비자기 회귀 모델이다. 결측치 대치 작업 시에는 미래값과 과거값 모두를 이용하여 양방향 모델을 훈련시킨다. 예를 들면, 순차적인 x1, x2, x3, x4, x5 값에 대하여 미리 알려진 값 x1과 x5를 이용하여 중간값인 x3을 먼저 예측하고, 이 정보를 이용하여 x1, x3값을 통해 x2를, x3, x5값을 이용하여 x4를 예측한다. 마지막으로는, 적대적 훈련을 통하여 전체적인 모델의 기능 향상을 이룬다.
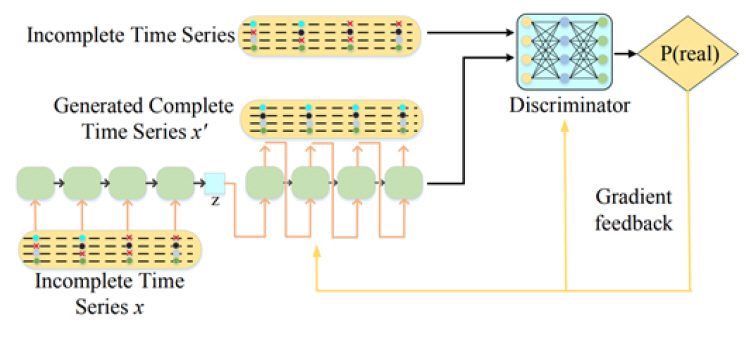
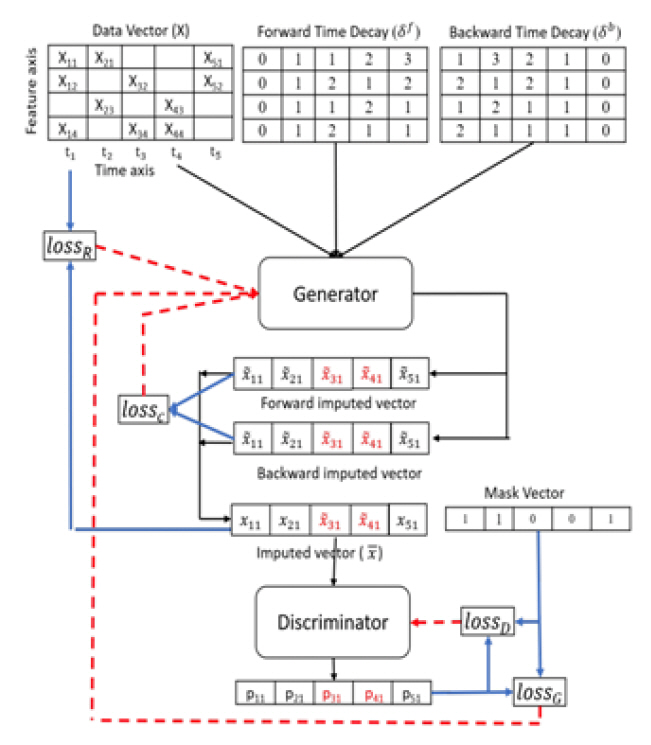
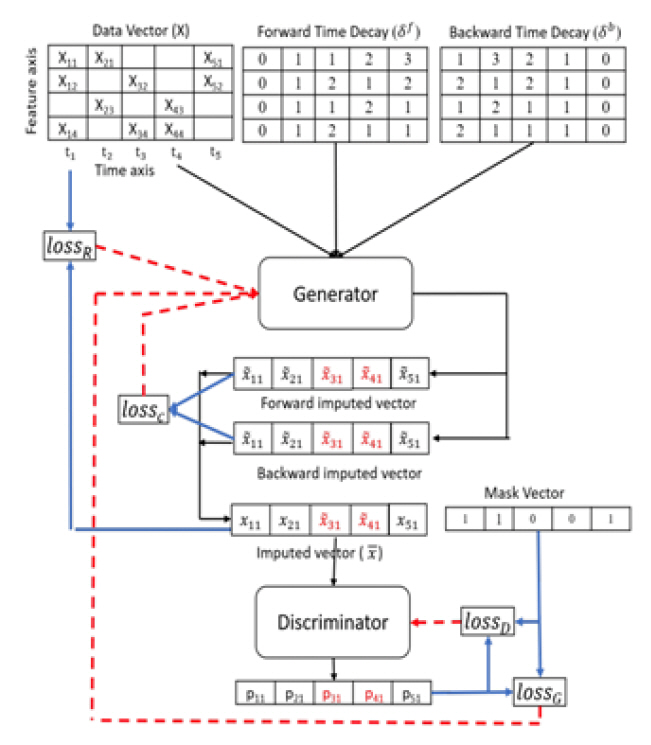
Bi-GAN(Bi-directional GAN)[25]은 그림 7에서 보여주는 아키텍처와 같이 생성적 적대 신경망을 양방향으로 반복적으로 진행하는 네트워크이다. 위의 단방향으로만 처리하는 경우보다 양방향적으로 처리하기 때문에 정확도가 더 높다. 또한, 이 모델은 정방향 역방향의 Time decay를 고려하기 때문에 다양한 길이의 시계열 결측 상황에 대하여 예측 작업이 유연하게 가능하다는 장점이 존재한다. 하지만 여전히 실시간으로 처리되기는 힘든 점이 있다.
Ⅳ. 결론
본고에서는 양질의 데이터 수집의 문제에 맞추어 데이터 결측치 처리에 관한 문제에 대해서 결측치의 종류, 그리고 결측치 처리 연구 동향에 대하여 기술 테마별로 정리해 보고 살펴보았다. 결측치 처리에 관한 연구는 지속적으로 진행되어 간단한 통계적인 기법부터 시작되어 머신러닝 그리고 최근에는 딥러닝의 최신 기술까지 응용되어 효과적인 결측치 처리 기술에 관하여 다양하게 소개되었다.
또한, 불규칙적으로 결측치가 발생하는 상황에서도 정확하게 대치 가능한 방법에 관한 연구와 개발이 활발하게 진행되었다. 그림 8에서는 데이터에 따라 방법들의 성능을 비교하여 가장 우수한 모델들을 소개한다.
그림 8
시계열 결측값 대치 기술 Benchmarks[265]
출처 https://paperswithcode.com/task/multivariate-time-series-imputation, CC-BY-SA.
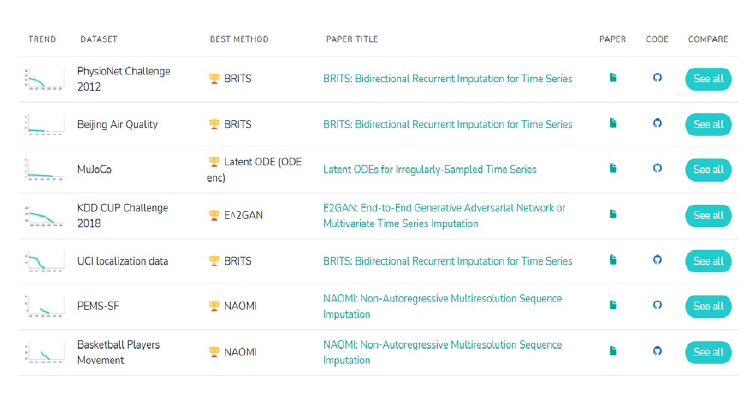
대부분의 경우 최근의 딥러닝 모델의 성능이 높은 것을 볼 수 있다. 하지만 딥러닝 기반 대치 방법은 모델을 훈련하거나 처리하는 시간이 많이 소요되는 점이 아직 실제상황 속에서 실시간으로 수집되고 있는 데이터에 적용하기에는 한계가 분명하다. 따라서 실상황에서 결측치 처리가 적용되기 위해서는 실시간적인 기능이 결합된 우수한 성능의 결측값 대치 방법이 필요하다. 앞으로는 다음과 같은 방향으로 결측치 처리 연구가 이루어질 필요성이 있다.
약어 정리
AI
Artificial Intelligence
AR
AutoRegressive
ARIMA
AutoRegressive Integrated Moving Average
Bi-GAN
Bi-directional Generative Adversarial Network
BRITS
Bidirectional Recurrent Imputation for Time Series
CDSA
Cross-Dimensional Self-Attention
E2GAN
End-to-end Generative Adversarial Network
GAIN
Generative Adversarial Imputation Network
GAN
Generative Adversarial Network
GRU
Gated Recurrent Unit
LATC
Low-Rank AutoRegressive Tensor Completion
MAR
Missing At Random
MCAR
Missing Completely At Random
MF
Matrix Factorization
MI
Multiple Imputation
MICE
Multiple Imputation using Chained Equations
MNAR
Missing Not At Random
M-RNN
Multi-directional Recurrent Neural Network
NAOMI
Non-Autoregressive Multiresolution Sequence Imputation
ODE
Ordinary Differential Equation
PSMF
Probabilistic Sequential Matrix Factorization
RNN
Recurrent Neural Network
SSIM
Sequence-to-Sequence Imputation Model
TRMF
Temperal Regularization Matrix Factorization
VAE
Variational AutoEncoder
A. Donders et al., "A gentle introduction to imputation of missing values," J. Clin. Epidemiol., vol. 59, no. 10, 2006, pp. 1087-1091.
S. Moritz et al., "ImputeTS: Time series missing value imputation in R," R J., vol. 9, no. 1, 2017, p. 207.
D.B. Rubin et al., "Multiple imputation for nonresponse in surveys," vol. 81, Wiley, Hoboken, NJ, USA, 2004.
B.N. Eskelson et al., "The roles of nearest neighbor methods in imputing missing data in forest inventory and monitoring databases," Scand. J. For. Res., vol. 24, no. 3, 2009, pp. 235-246.
I.R. White et al., "Multiple imputation using chained equations: Issues and guidance for practice," Stat. Med., vol. 30, no. 4, 2011, pp. 377-399.
A. Mnih et al., "Probabilistic matrix factorization," Adv. Neural Inf. Process. Syst., vol. 20, 2007, pp. 1257-1264.
H. Yu et al., "Temporal regularized matrix factorization for high-dimensional time series prediction," in Proc. Int. Conf. Neural Inf. Process. Syst., Barcelona, Spain, Dec. 2016, pp. 847-855.
A. Agarwal et al., "Model agnostic time series analysis via matrix estimation," in Proc. ACM Meas. Anal. Comput. Syst., vol. 2, no. 3, 2018, pp. 1-39.
Ö.D. Akyildiz et al., "Probabilistic sequential matrix factorization," arXiv preprint, CoRR, 2019, arXiv:1910.03906
Z. Zhang, "Missing data imputation: Focusing on single imputation," Ann. of transl. med., vol. 4, no. 1, 2016.
G.E. Box et al., "Time series analysis: Forecasting and control," Wiley, Hoboken, NJ, USA, 2015.
X. Chen et al., "Low-rank autoregressive tensor completion for multivariate time series forecasting," arXiv preprint, CoRR, 2020, preprint arXiv:2006.10436
J. Yoon et al., "Estimating missing data in temporal data streams using multi-directional recurrent neural networks," IEEE Trans. Biomed. Eng., vol. 66, no. 5, 2018, pp. 1477-1490.
Z. Che et al., "Recurrent neural networks for multivariate time series with missing values," Sci. Rep. vol. 8, no. 1, 2018, pp. 1-12.
W. Cao et al., "Brits: Bidirectional recurrent imputation for time series," arXiv preprint, CoRR, 2018, arXiv:1805.10572
Y.F. Zhang et al., "SSIM—A deep learning approach for recovering missing time series sensor data," IEEE Internet Things J., vol. 6, no. 4, 2019, pp. 6618-6628.
Y. Rubanova et al., "Latent odes for irregularly-sampled time series," arXiv preprint, CoRR, 2019, arXiv:1907.03907
J. Ma et al., "CDSA: Cross-dimensional self-attention for multivariate, geo-tagged time series imputation," arXiv preprint, CoRR, 2019, arXiv:1905.09904
J. Yoon et al., "Gain: Missing data imputation using generative adversarial nets," in Proc. Int. Conf. Mach. Learn. (PMLR), Stockholm, Sweden, July 2018, pp. 5689-5698.
Y. Luo et al., "Multivariate time series imputation with generative adversarial networks," in Proc. Int. Conf. Neural Inf. Process. Syst., 2018, pp. 1603-1614.
Y. Luo et al., "E2gan: End-to-end generative adversarial network for multivariate time series imputation," AAAI Press, 2019, pp. 3094-3100.
Y. Liu et al., "Naomi: Non-autoregressive multiresolution sequence imputation," arXiv preprint, CoRR, 2019, arXiv:1901.10946
M. Gupta et al., "Time-series imputation and prediction with bi-directional generative adversarial networks," arXiv preprint, CoRR, 2020, arXiv:2009.08900
그림 1
(a) GRU의 구조, (b) GRU-D의 구조, (c) GRU-D의 전체 모델 아키텍처[16]
출처 Z. Che et al., “Recurrent neural networks for multivariate time series with missing values,” Scientific Reports, vol. 8, no. 1, 2018, pp. 1-12, CC BY 4.0,
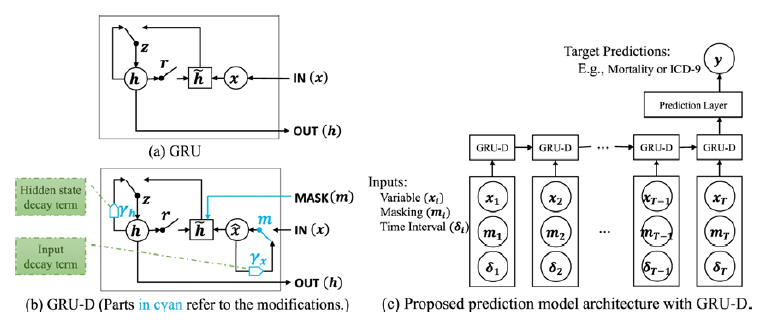
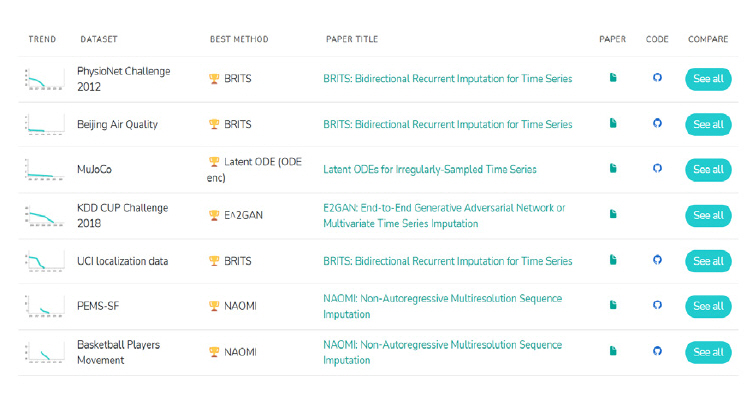
그림 8
시계열 결측값 대치 기술 Benchmarks[265]
출처 https://paperswithcode.com/task/multivariate-time-series-imputation, CC-BY-SA.
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.