김현우 (Kim H.W.)
오유리 (Oh Y.R.)
나중찬 (Na J.C.)
Ⅰ. 서론
동형암호 기술은 양자컴퓨터의 공격에도 안전한 격자 문제(Lattice Problem) 기반 암호 체계이면서 기반 난제로 R-LWE(Ring-Learning with Error)를 적용하여 강도 높은 보안성을 갖추고 있다. 뿐만 아니라 동형암호는 동형연산(Homomorphic Operation)이라는 수학적 특성을 활용하여 암호화된 데이터에 대해서도 결합 및 연산 처리를 가능하게 한다. RSA(Rivest, Shamir, and Adleman), ECC(Elliptic Curve Cryptography), AES(Advanced Encryption Standard) 등과 같은 기존 암호 시스템은 데이터의 결합 및 연산 처리를 위해 암호 데이터를 복호하여 재식별해야 하므로, 이 과정에서 민감한 정보가 노출될 수밖에 없는 기술적 한계가 있었다.
동형암호 기술은 데이터를 암호화된 상태로 저장, 전송, 결합 및 연산 처리하여 전체 데이터 흐름에서 재식별화 처리가 불필요하다는 특성을 갖추고 있다. 따라서 동형암호 기술은 데이터의 높은 보안성 제공과 민감한 데이터의 안전한 활용성 제공이라는 상충된 요구사항을 모두 충족하는 기술로 각광받고 있다.
동형암호 기술에는 BGV(Brakerski, Gentry, and Vaikuntanathan), BFV(Brakerski, Fan, and Vercauteren), CKKS(Cheon, Kim, Kim and Song) 등 다양한 암호 스킴(Scheme)이 있다. 이러한 동형암호 기술들은 기반 난제인 R-LWE 정의에 의해 메시지를 암호화하는 과정에서 메시지를 n차 다항식 쌍으로 매핑하고, Error 다항식이라 불리는 노이즈 값을 더하며, 암호키 다항식을 메시지 다항식에 포함시키는 등의 암호화 연산 처리 과정을 통해서 암호문을 생성하게 된다. 따라서 동형암호는 메시지의 안정성을 크게 향상시키지만, 암호화 과정에서 암호문들의 사이즈가 매우 커지며 암호문에 추가된 노이즈 값 등이 암호문 간의 연산을 반복할수록 원래의 메시지를 침범하게 되므로 이를 막기 위한 부가적인 연산들도 추가로 필요하게 된다. 이러한 이유로 연산량이 대폭 늘어나는 탓에 느린 연산 처리 문제를 해결하여 실용적 수준으로 빠르게 연산 처리 결과를 제공해야 하는 기술 개발의 숙제도 가지고 있다.
동형암호의 결과를 얻기까지 긴 연산 시간, 즉 느린 연산 처리 문제를 해결하기 위한 연구로는 수학적으로 연산량을 줄여 연산의 효율성을 향상시키는 기법을 도입하거나 고안하는 연구들과 동형 암호 전용 연산 처리 가속 하드웨어 기술에 대한 연구들이 있다. 인공지능의 연산 처리 가속 하드웨어 연구 분야에서 GPU(Graphics Processing Unit)를 활용하거나 ASIC(Application Specific Integrated Circuit)를 개발하여 연산 처리 가속에 적용하는 등의 연구가 활발한 것과 비슷하게 동형암호의 경우도 연산 처리 가속 하드웨어 기술 연구가 급부상하고 있다.
따라서 본고에서는 다양한 동형암호 스킴을 위한 연산 처리 가속 하드웨어 기술 연구 동향과 집중 연구되고 있는 동형암호의 주요 연산 처리 가속 하드웨어 기술에 대해서 고찰해 본다. Ⅱ장에서는 다양한 동형암호 스킴들을 위한 연산 처리 가속 하드웨어 기술 연구 동향을 소개한다. Ⅲ장에서는 한국전자통신연구원의 동형암호 연산 처리 가속 하드웨어 기술 연구 방향에 대해서 소개하고, Ⅳ장을 결론으로 하여 완전 동형암호 하드웨어 가속기 기술에 대해서 소개한다.
Ⅱ. 동형암호 연산 가속 하드웨어 기술
1. BGV 스킴을 위한 연산 하드웨어
가. BGV 스킴 소개
BGV 동형암호 시스템은 암호문 상위비트에 노이즈 값이 추가되는 특성으로 인해 암호문들의 다수 연산 처리에도 불구하고 사이즈가 커진 노이즈 값이 메시지 값을 쉽게 침범하지 않는다. 그러나 암호문들의 거듭되는 연산으로 인해 모듈러스가 축소되므로 지속 연산이 가능한 수준의 모듈러스 한계, 즉 관리 가능한 수준의 모듈러스 최대값에 노이즈 값의 크기가 도달하고 있는지를 추적하고, 한계에 도달한 암호문 모듈러스를 회복시키는 모듈러스 스위칭(Modulus Switching)이라는 부가적인 연산을 수행해야 한다. 물론 이 과정에서 동형암호의 특성인 암호화된 상태의 연산 보장을 위해 암호키 변경(Key Switching)이라는 과정도 필요하게 된다. BGV 동형암호 스킴의 연산에는 Key Generation(Secret Key, Public Key, Evaluation Key), Encryption, Decryption, Homomorphic Evaluation(Homomorphic Mult./Add./Sub.), Key Switching, Modulus Switching이 있다.
• ParamGen(λ, P, K, B) → Params
- P, p > 1 : integer, plaintext modulus
- K ≥ 1 : integer, vector length
- B : multiplicative depth
- λ : security level
- n : degree parameter
- q : ciphertext modulus
- ∝ : standard deviation
• SecKeygen(params) → SK, EK
- SK : secret key, an element “s” chosen from key distribution “D1” ring R
- EK : there is no evaluation key.
• PubKeygen(params) → SK, PK, EK
- SK : secret key, an element “s” chosen from key distribution “D1”, an element “s” that belong to the R.
- PK : chooses a uniformly random elements a from the ring R/pR and outputs the pair of ring elements.
ex, PK = (a, b) = (-a, a×s + p×e)
- e : is chosen from the error distribution “D2”.
• SecEncrypt(SK, M) → C
- First, maps the message M which comes from the plaintext space
- Second, samples a uniformly random element a from the ring R/pR and outputs the pair of ring elements.
(c0, c1) = (-a, a×s + p×e +
- e : is chosen from the error distribution “D2”.
• PubEncrypt(PK, M) → C
- First, maps the message M which comes from the plaintext space
- Second, samples three uniformly random elements r from distribution “D1 ” and f and f' from the error distribution “D2” and outputs the pair of ring elements.
(c0, c1) = (-a×r + p×f, b×r + p×f' +
• Decrypt(SK, C) → M
- First, computes the ring element c0×s + c1 over R/pR.
- Second, interprets it as an element c' in the ring R.
- It them computes c'(mod p), an element of R/pR, which it outputs → M.
SecEncrypt는 Secret Key SK를 사용하여 메시지 M을 암호문으로 변환하는 과정이다. 첫 번째로 메시지 M은 정수
Decrypt는 메시지 M을 복호화하는 과정이며, 우선 암호문을 이용하여 c0×s + c1을 계산하고, 그 결과를 Ring의 원소로 c' 변환한다. 그 후 c'와 p의 모듈로 연산(c' mod p)을 수행하면, 메시지 매핑 과정에서 사용한 Plaintext Modulus p로 정의되는 Ring R/pR 의 원소로 변환되어 출력된다. 이 결과를 메시지 매핑의 역순으로 변환하면 원래의 메시지 M이 된다. 이러한 과정에서
더불어 암호문의 연산(Homomorphic Evaluation)에는 Ciphertext Modulus Switching, Key Switching 등의 부가적 연산 또한 필요하게 된다. 예를 들어 n차 다항식들 간의 곱셈 연산은 연산 복잡도가 O(n2) 수준의 Polynomial Complexity를 갖으며, 이러한 연산 복잡도를 갖는 동형암호 스킴들을 쉼 없이 연산 처리해야 하는 부담이 있으므로 이를 해결할 방법이 필요하다.
나. BGV 시스템 연산 가속 하드웨어 기술
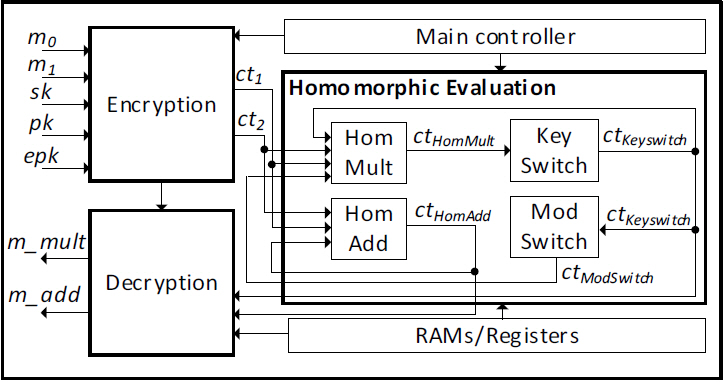
동형암호 시스템의 긴 연산 처리 시간을 단축하기 위해 그림 1과 같이 Yang 등[1]은 FPGA를 활용한 BGV 스킴용 동형암호 연산 처리 가속 하드웨어 기술을 제안하였으며, 하드웨어 블록도 수준으로 구조를 소개하였다.
동형암호 시스템은 일반적으로 Key Generation, Encryption, Decryption 등의 연산 유닛을 갖추고 암호키 생성, 데이터 암호화 및 복호화 역할을 수행하는 Client와 Homomorphic Evaluation 연산 유닛을 갖추고 암호 데이터의 연산 처리 역할을 수행하는 Cloud Computation 도메인으로 분리하여 구조를 설계하지만, 그림 1에서는 분리하지 않고 통합된 구조를 보여주고 있다.
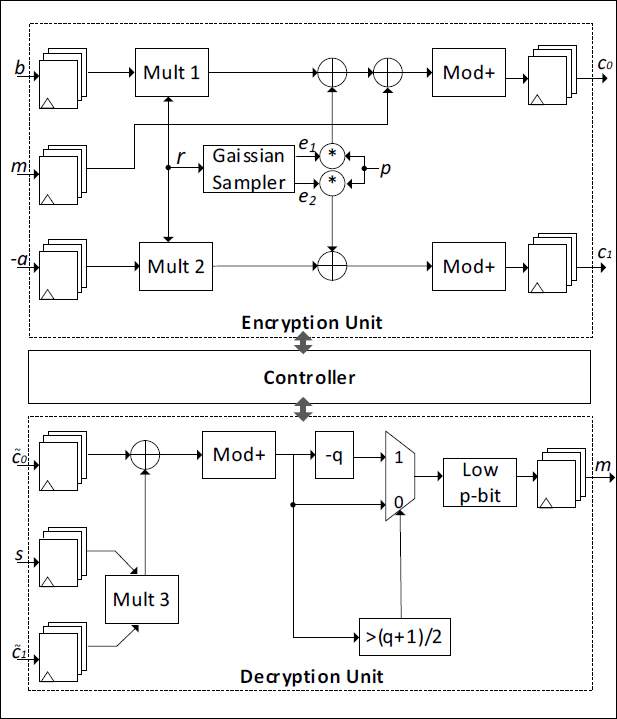
그림 1에서의 Encryption Unit과 Decryption Unit의 상세구조도를 그림 2에 나타내었다. Encryption Unit은 앞서 소개했던 BGV 스킴의 연산들 중 “Pub Encrypt(PK, M) → C”에 대응하며, 그림에 보이는 바와 같이 메시지 m과 Gaussian Sampler를 통해 추출된 노이즈 값 r, e1, e2 에 plaintext modulus p가 곱해진 p × e1 가 더해져서 메시지 상위 워드에 노이즈 값이 추가된 암호문 (c0, c1) = (-a×r + p×f, b×r + p×f' +
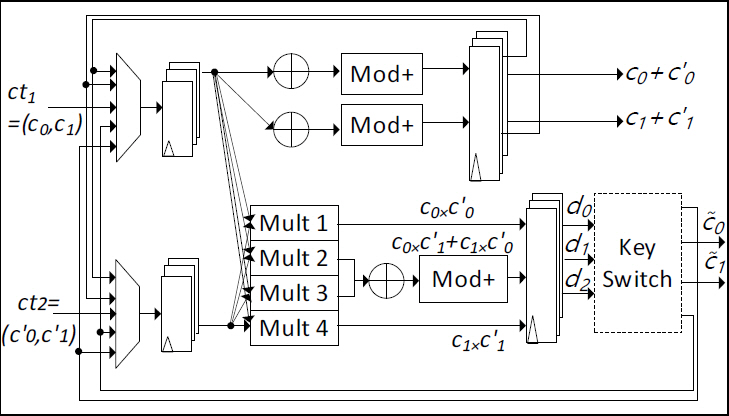
그림 1에서의 Homomorphic Evaluation을 구성하는 HomMult, HomAdd의 상세구조도는 그림 3에 나타내었고, KeySwitch의 상세구조도는 그림 4에 나타내었다.
HomAdd는 Homomorphic Addition을 처리하는 Unit이며, 암호문 ct1=(c0, c1)과 암호문 ct2=(c'0, c'1) 간의 덧셈을 수행한다. 이를 통해 암호문 ct1과 ct2를 구성하는 좌측 다항식(c0, c'0) 간의 덧셈과 우측 다항식(c1, c'1) 간의 덧셈에 대한 결과 다항식 ct=(c0+c'0, c1+c'1)을 얻게 된다.
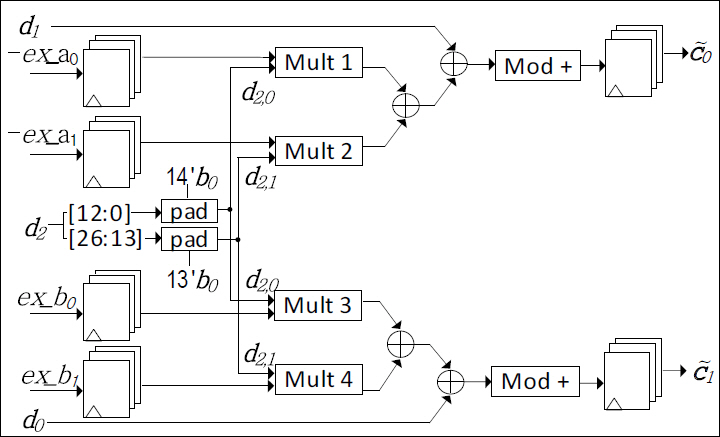
HomMult는 Homomorphic Multiplication을 처리하는 Unit이며, 암호문 ct1=(c0, c1)과 암호문 ct2=(c'0, c'1) 간의 곱셈을 수행한다. 이를 통해 암호문 ct1과 ct2 간의 곱셈 결과 ctHomMult=(d0, d1, d2)=(c0×c'0, c1×c'1, c0×c'1+c1×c'0)를 얻는다. 그림 4의 Key Switch Unit을 통해 EK(Evaluation Key)=(ek0, ek1)=(-ex_a, ex_b)와 ctHomMult 간의 연산을 수행하고, 지속적인 암호문 간의 연산을 위한 수단인 ctKeySwitch=(
2. BFV 스킴을 위한 연산 하드웨어
가. BFV 스킴 소개
BFV 동형암호 시스템은 암호문 하위비트에 노이즈 값이 추가되는 특성으로 인해, 암호문들에 대해 반복 연산을 수행하면 사이즈가 커진 노이즈 값이 메시지 값을 침범하게 된다. 그러므로 암호문들의 반복되는 연산으로 인한 노이즈 값이 메시지 값을 침범하지 않는 수준까지만 연산을 수행하도록 연산 횟수를 제한해야 한다. 이는 노이즈 값의 크기를 추적하고 한계에 도달한 암호문의 노이즈 크기를 축소하는 Reboot 또는 Bootstrapping, 또는 Relinearization이라고 부르는 부가적인 연산을 통해 수행된다. 물론 이 과정에서 BGV와 마찬가지로 동형암호의 특성인 암호화된 상태의 연산 보장을 위해 암호키 변경이라는 과정도 필요하게 된다. BFV 동형암호 스킴의 연산에는 Key Generation(Secret Key, Public Key, Evaluation Key), Encryption, Decryption, Homomorphic Evaluation(Homomorphic Mult./ Add./Sub.), Key Switching, Relinearization이 있다.
• ParamGen(λ, P, K, B) → Params
- P, p > 1 : integer, plaintext modulus
- K ≥ 1 : integer, vector length
- B : multiplicative depth
- λ : security level
- n : degree parameter
- q : ciphertext modulus
- T, L : integer, L = logTq, T is the bit- decomposition modulus.
- W : integer W=⌊q/p⌋
- ∝ : standard deviation
• SecKeygen(params) → SK, EK
- SK : secret key, an element “s” chosen from key distribution “D1” ring R.
- ai : sample a random ai from R/pR, i = 1,...,L.
- ei : sample a error ei from D2.
- EK : (EK1,..., EKL) EKi = (-(ai × s + ei)+ Ti × s2, ai)
• PubKeygen(params) → SK, PK, EK
- SK : secret key, an element “s” chosen from key distribution “D1”, an element “s” that belong to the R.
- PK : chooses a uniformly random elements a from thering R/pR and outputs the pair of ring elements.
ex, PK = (-(a×s + e), a)
- e : is chosen from theerror distribution “D2”.
- ai : sample a random ai from R/pR, i = 1,...,L.
- ei : sample a error ei from D2.
- EK : (EK1,..., EKL)
EKi = (-(ai × s + ei)+ Ti s2, ai)
• PubEncrypt(PK, M) → C
- First, maps the message M which comes from the plaintext space
PK=(-(a×s + e), a)=(pk0, pk1)
- Second, samples secret u random element from distribution D1 and e1, e2 from theerror distribution D2 and outputs the pair of ring elements.
(c0, c1) = (pk0 ×u+e1+W×
• SecEncrypt(SK, M) → C
- C(s ) = W×
• Decrypt(SK, C) → M
- First, The message
- Second, rounding each coefficient to the nearest integer, and reducing each coefficient modulo p.
- It them computes c'(mod p), an element of R/pR, which it outputs → M.
BFV 스킴의 연산들 또한 이전에 소개한 BGV 스킴의 연산들과 같이 다항식들 간의 연산이라는 점은 동일하지만, 연산 방식은 다소 차이가 있다. BFV와 BGV의 주요한 차이점으로는 암호문을 구성할 때 노이즈 값을 추가하는 위치가 다르다는 점이며, BGV는 메시지의 상위에 노이즈 값을 추가하고 BFV는 하위에 노이즈 값을 추가한다. 또한 암호문 간의 곱셈을 수행하는 방식에 있어 BGV는 Mod q 공간상에서 연산을 수행하지만, BFV는 정수(Integers) 공간상에서 연산을 수행한 후 Round 연산 및 Mod q 연산을 통해 결과 암호문 C를 얻는다(
나. BFV 스킴 연산 가속 하드웨어 기술
BFV 스킴을 FPGA를 활용하여 구현한 Rashmi Agrawal 등[2]은 Client와 Cloud Computation의 역할로 분할하여 동형암호 연산 처리 가속 하드웨어 구조를 설계하였다.
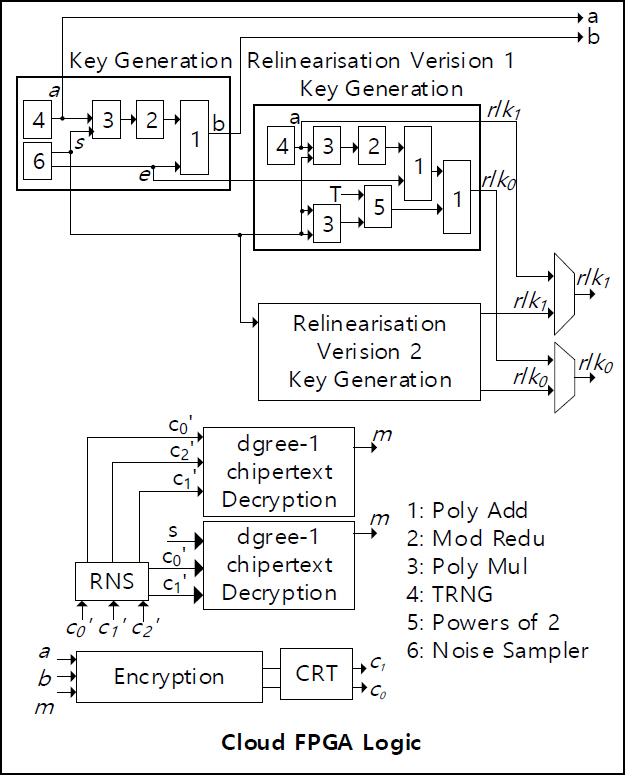
그림 5에서는 Client용 동형암호 연산 처리 가속 하드웨어의 구성들을 볼 수 있다. Client 가속 하드웨어는 Key Generation, Encryption, Decryption 등의 연산 유닛을 갖추고 암호키 생성, 데이터 암호 및 복호 처리를 수행한다.
그림 5의 Key Generation Unit은 앞서 소개했던 BFV 스킴 연산들 중 PubKeygen(params) → SK, PK, EK 연산을 수행하는 PK Key Generation Unit이다. Key Generation Unit은 PK=(-(a×s+e), a)=(pk0,pk1) 연산을 수행하기 위해 TRNG(True Random Number Generator)를 통해 a를 생성하고, Noise Sampler를 통해 Secret Key s와 e 노이즈 값들을 획득한다. Poly MUL을 통해 a×s Polynomial Multiplication(a×s+e)을 수행하고, Poly Add를 통해 e를 더함으로써 PK를 생성한다.
Relinearisation Version 1 Key Generation Unit은 EKi = (-(ai × s + ei)+ Ti s2, ai), EK : (EK1,..., EKL)의 연산을 수행하기 위해 TRNG를 통해 ai를 생성하고, PK Key Generation Unit에서 Noise Sampler를 통해 Secret Key s와 ei 노이즈 값들을 획득한다. 그 후 생성 및 획득된 값들을 이용하여 (ai × s + ei)+ Ti s2 연산을 처리하고 EK를 생성한다. Encryption Unit과 Ciphertext Decryption Unit에 대한 설명은 생략한다.
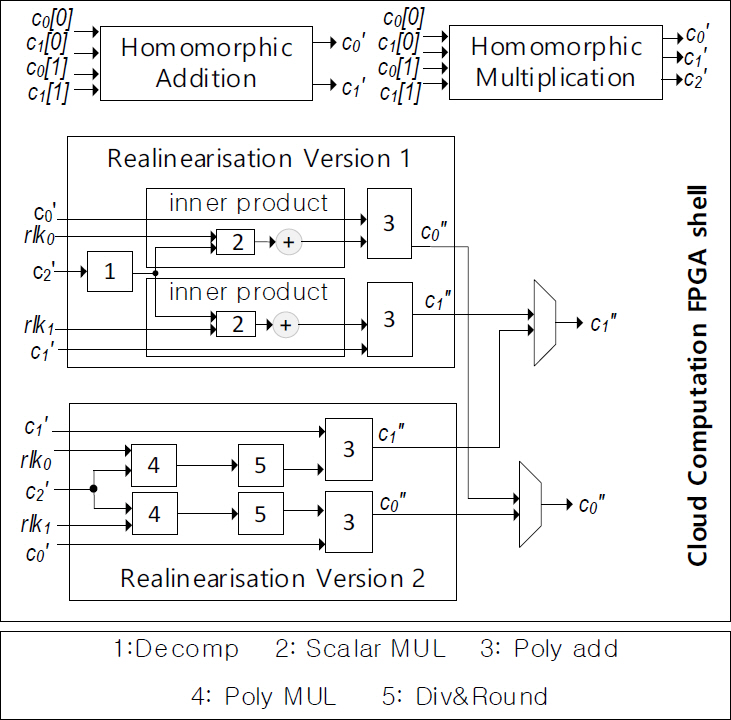
그림 6은 Cloud Computation의 Homomorphic Evaluation 연산 처리 가속을 위한 구성들을 나타낸다. 구성 Unit에는 Homomorphic Multiplication Unit, Homomorphic Addition Unit, Relinearisation Unit이 있다. Relinearisation Unit은 암호문 상태의 연산을 지속하기 위해, 반복된 연산을 통해 커진 노이즈 값을 축소하는 연산을 수행한다.
Relinearisation Version 1과 2 Unit은 앞서 소개한 Client를 구성하는 Relinearisation Version 1과 2, 그리고 Key Generation Unit에서 생성한 EK : (EK1,..., EKL), EKi = (rlk0i, rlk1i) = (- (ai × s + ei)+ Ti s2, ai)를 이용하여 R/pR Ring상에서
3. CKKS 스킴을 위한 연산 하드웨어
가. CKKS 스킴 소개
CKKS 동형암호 스킴[3]은 암호문 하위비트에 노이즈 값이 추가되는 특성으로 인해, 암호문들의 반복 연산 횟수가 누적되면 사이즈가 커진 노이즈 값이 메시지 값을 침범하게 되는 성질은 BFV 스킴과 유사하다. 그러므로 BFV 스킴과 같이 암호문들의 반복되는 연산으로 인해 노이즈 값이 메시지 값을 침범하지 않는 수준까지만 반복 연산이 수행되도록 연산 횟수를 제한해야 한다. 따라서 CKKS 스킴 역시 노이즈 값의 크기를 추적하고, 한계에 도달한 암호문의 노이즈 크기를 축소하는 부가적인 Bootstrapping 또는 Relinearization 연산을 수행해야 한다.
BGV나 BFV 스킴은 암호문에 대해 거듭된 연산이 수행되더라도 암호문에 추가된 노이즈 값은 정밀하게 관리된다. 즉, 암호문 모듈러스가 설정된 값 미만으로 유지되도록 암호문 반복 연산 횟수를 관리하거나, 노이즈 값이 암호문의 메시지 값 영역까지 침범하지 않을 연산 횟수 미만으로 관리하게 되므로 반복되는 연산 횟수에 제한이 있었다. 그러나 CKKS 스킴에서는 반복 연산 횟수를 크게 늘리기 위해 Rescaling이라는 연산을 추가로 고안하였다. 모듈러스 크기를 증가시킨 암호문 메시지 하위비트에 Security Level을 유지할 수 있는 크기의 작은 노이즈 값을 추가하고, 반복된 연산을 수행하면서 메시지 값과 노이즈 값이 Security Level을 취약하게 하지 않는 수준에서 암호문을 근사치 계산, 즉 Rounding 연산을 수행하여 암호문의 사이즈를 낮추는 방법이다. Rescaling은 BFV의 Modulus Switching과 유사해 보이지만 용도는 다르다. 예를 들어, 메시지 m의 암호문 c를 <c, sk>, = m + e (modq) 라 하면, Rescaling의 출력 값인 암호문 c'은 ⌊p-1 ∙ c⌉ (mod q/p)이 된다. 즉 노이즈 값 e/p를 갖는 유효한 암호문 m/p가 되어, 암호문의 모듈러스 크기를 줄임과 동시에 노이즈 값의 위치를 메시지의 LSB 쪽으로 이동시키게 된다. 이것은 마치 고정 또는 부동 소수점 산술 연산의 Rounding 과정과 유사하다. 메시지에 추가된 노이즈 값은 메시지의 크기에 비해 미미한 크기이므로 차후 메시지를 복호화할 때는 가장 가까운 거리의 값을 취하는 방식을 적용한다. 이런 근사치 계산을 고안함으로써 반복되는 연산 횟수를 BFV 스킴보다 증가시킬 수 있다는 점으로 인해 CKKS 스킴은 인공지능과 같이 암호문에 대해 반복 연산 횟수가 많은 응용 분야에서 프라이버시를 보장하는 수단으로 선호되고 있다.
CKKS 동형암호 스킴의 연산에는 Key Generation(Secret Key, Public Key, Evaluation Key), Encryption, Decryption, Homomorphic Evaluation(Homomorphic Mult./Add./Sub.), Key Switching, Rescaling, Relinearization이 있다.
CKKS 동형암호 스킴의 연산에는 Key Generation(Secret Key, Public Key, Evaluation Key), Encryption, Decryption, Homomorphic Evaluation(Homomorphic Mult./Add./Sub.), Key Switching, Rescaling, Relinearization이 있다.
• ParamGen(λ, n, q, p) → Params
- λ : security level
- n : ring size
- q : ciphertext modulus
- p : special modulus p coprimeto q
- χ : key distribution
- Ω : error distribution Ω over R
• SecKeyGen() → SK
- SK : secret key, an element “s” chosen from key distribution “χ.” ring R.
• PubKeyGen() → SK, PK
- SK : secret key, an element “s” chosen from key distribution “χ.” ring R=Rqp.
- PK : chooses a uniformly random elements a from thering R/pR =U(Rqp) and outputs the pair of ring elements.
ex, PK = (-(a×s + e), a)
- e : is chosen from theerror distribution “Ω”.
• SymEnc(m, SK)
-
- SK : secret key, an element “s” chosen from key distribution “χ.” ring R=Rqp.
- PK : chooses a uniformly random elements a from thering R/pR =U(Rqp) and outputs the pair of ring elements.
ex, PK = (-(a×s + e), a)
- e : is chosen from theerror distribution “Ω”.
- C : return the ciphertext ct = (c0, c1) = (b, a).
• EvalKeygen() → SK, PK, EK
- SK : secret keys, elements s, s' chosen from key distribution “χ.” ring R=Rqp.
- g : gadget vector g = Zd
- EK :
• HomAdd(ct0, ct1)
- Given ciphertexts
• Mod(x, p)
- For a modulus p with at most w bits, given an integer x ∈ [0, (p - 1)2 ]
- Precompute u = ⌊22w/p⌋, and compute z = x (mod p).
- Mod(a, p) performs Mod(ai, p) for all i = 0, 1,..., n - 1.
• MulRed(x, y, y', p)
- For w-bit words and a modulus p < 2w-2, given x, y ∈ Zp and precomputed y'= ⌊y ∙ 2w/p⌋, compute x · y (mod p).
나. CKKS 스킴 연산 HW 가속 기술
CKKS 스킴을 FPGA를 활용하여 구현한 M. Sadegh Riazi 등[4]은 Cloud Computation을 위한 CKKS 스킴용 동형암호 연산 처리 가속 하드웨어 구조를 설계하였다.
그림 7은 Cloud Computation을 위한 동형암호 연산 처리 가속 System 구성들을 보인다. Homomorphic Evaluation은 Homomorphic Mult./Add./Sub., Key Switching, Rescaling, Relinearization이 주요 연산들이며, 특히 암호문의 Polynomial들 간 연산을 위한 MULT, NTT, INTT Unit들과 Relinearization 연산을 위한 KeySwitch Unit들을 FPGA에 구현하였다.
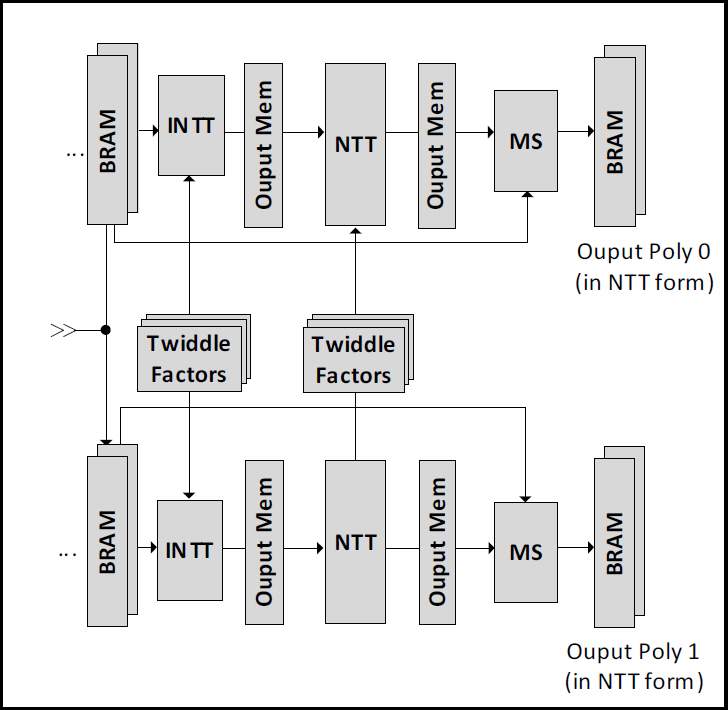
CKKS 스킴에서 대표적으로 중요한 연산이 Rescaling이며, 그림 8의 MS Unit: Modulus Switching에 포함되어 있다. 암호문 간의 Homomorphic Multiplication과 Modular 연산을 고속·병렬 처리하기 위해 수학적 기법인 NTT(Number Theoretic Transform)과 RNS(Residue Number System)을 도입하여 변환을 통해 분할된 계수들을 독립적으로 병렬 연산이 가능하게 하였다. MS Unit에서는 연산한 결과 암호문
그림 8의 INTT→NTT→MSUnit으로 이어지는 연산은 NTT와 RNS 변환 및 분할된 다항식의 계수들 간의 Modulus Switching 연산을 수행하며, 이를 통칭하여 Flooring 연산이라 한다. Flooring 연산의 입력과 출력은 각각
• Floor(
- INTT :
-
-
Ⅲ. ETRI 완전동형암호 가속 기술
1. FHE 시스템을 위한 연산 하드웨어
가. 주요한 성능 목표 소개
기존 CPU, GPU, FPGA가 내장하고 있는 ALU나 연산기들은 LAWS(Large Arithmetic Word Size) 연산, 고차 다항식들 간 연산, Modular 연산 등과 같이 완전동형암호(FHE: Fully Homomorphic Encryption) 시스템에 요구되는 연산들과 다양한 완전동형암호 스킴들에 호환적으로 적용될 수 있는 연산기를 구현하는 데 구조적 한계가 있어 동형암호 연산 처리에 부적합하였다. 한국전자통신연구원에서는 이러한 한계를 극복하기 위해 대량 데이터의 결합 연산 등 막대한 연산량을 요구하는 Cloud Computation 전용 완전동형암호 ASIC과 프리미티브 라이브러리 및 SW를 포함하는 완전동형암호 가속 기술을 개발하고 있다. 뿐만 아니라 완전동형암호 가속 기술을 적용한 인공지능 실증 사례 구축을 위해, 클라우드 서버상에서 HW 가속 기술을 지원하는 프라이버시 보장 암호데이터 인공지능 고속 처리 기술까지를 목표로 기술 개발을 수행하고 있다.
나. 기술 소개
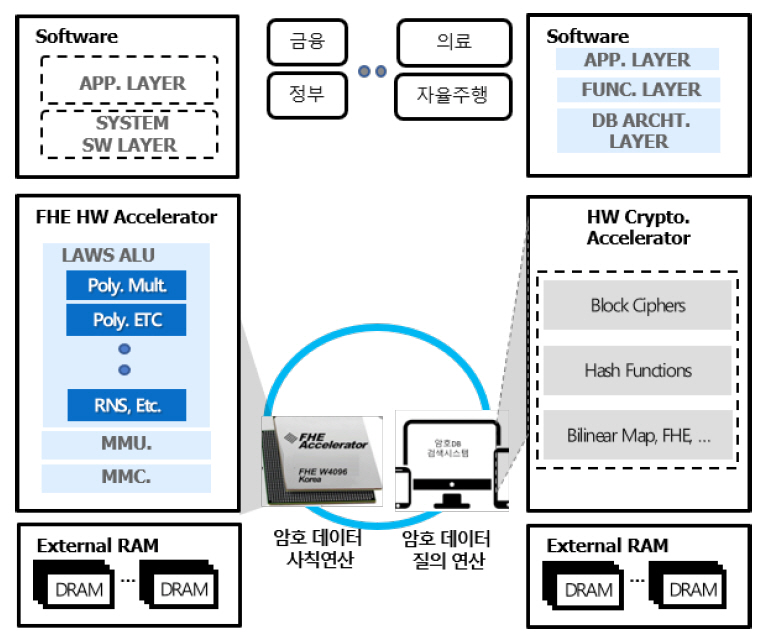
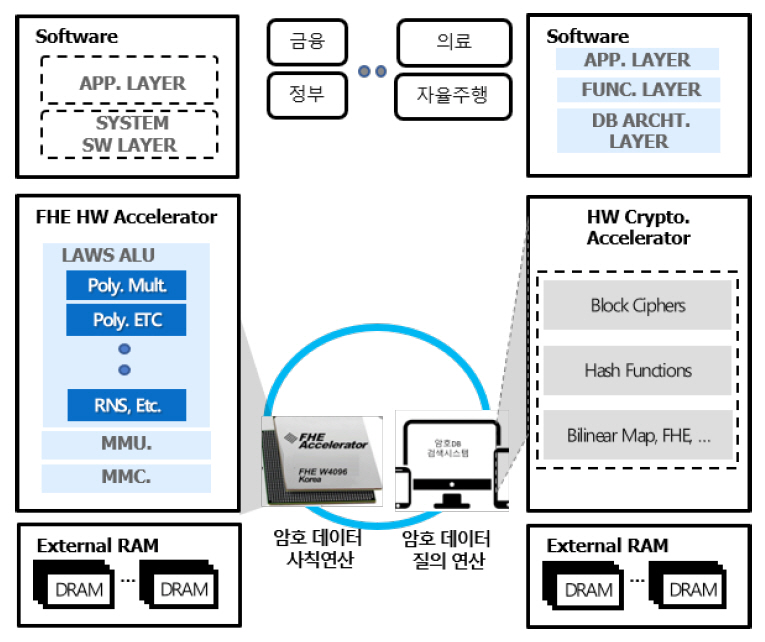
그림 9의 FHE Accelerator는 앞서 주요한 성능 목표 소개를 통해 제시한 완전동형암호 스킴에 최적화된 전용 연산기를 탑재한 HW 가속기 칩셋으로써 동형암호화된 데이터, 즉 암호문 연산 시간이 기존 CPU나 GPU가 암호화되지 않은 데이터를 연산하는 데 소요하는 시간 수준으로 연산 가속 성능을 달성하게 된다.
Ⅳ. 결론
BGV, BFV, CKKS 등 다양한 동형암호 스킴들이 소개되었다. 동형암호는 큰 워드 사이즈 데이터들의 연산, 고차 다항식들 간의 사칙연산, 모듈러 연산과 같이 높은 복잡도를 갖는 연산들로 인해 연산 결과를 얻기까지 긴 시간이 소요되는 특성을 가지며, 이는 실용화를 더디게 하는 주요한 이유이다. 이러한 긴 연산 시간을 단축하기 위해 병렬 연산 구조를 통한 연산 가속 처리와 NTT, RNS 등 수학적 연산 효율화 기법들을 활용하여 구현한 동형암호 연산 하드웨어 기술들이 활발하게 연구되고 있다.
DNA(Data-Network-AI)로 이어지는 4차산업혁명, 그리고 일명 “데이터3법”, “마이데이터법” 등이 제정된 상황 속에서 양자컴퓨터의 공격에도 안전한 수준의 민감 데이터 보호와 인공지능 등의 서비스에 데이터 활용이라는 상충된 요구사항을 동시에 수용할 수 있는 동형암호 기술은 향후에도 지속적으로 주목받을 수밖에 없다. 동형암호를 실용적 수준으로 끌어올리기 위해서는 범용성을 갖고 다양한 응용에 적용될 수 있도록 다양한 동형암호 시스템들을 호환적으로 구현하는 동형암호 하드웨어 연산 가속 기술 연구와 이를 구동하는 소프트웨어와 API(Application Program Interface)에 관한 연구가 중요하다.
약어 정리
AES
Advanced Encryption Standard
ASIC
Application Specific Integrated Circuit
BFV
Brakerski-Fan-Vercauteren
BGV
Brakerski-Gentry-Vaikuntanathan
CKKS
Cheon-Kim-Kim-Song
ECC
Elliptic Curve Cryptography
FHE
Fully Homomorphic Encryption
GPU
Graphics Processing Unit
LAWS
Large Arithmetic Word Size
NTT
Number Theoretic Transform
R-LWE
Ring-Learning With Error
RNS
Residue Number System
RSA
Rivest-Shamir-Adleman
참고문헌
그림 1
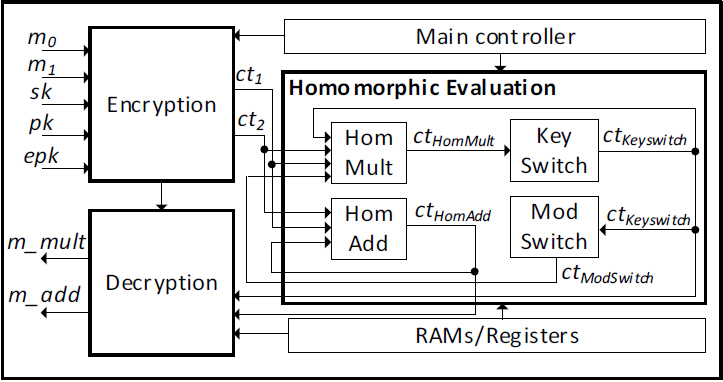
그림 2
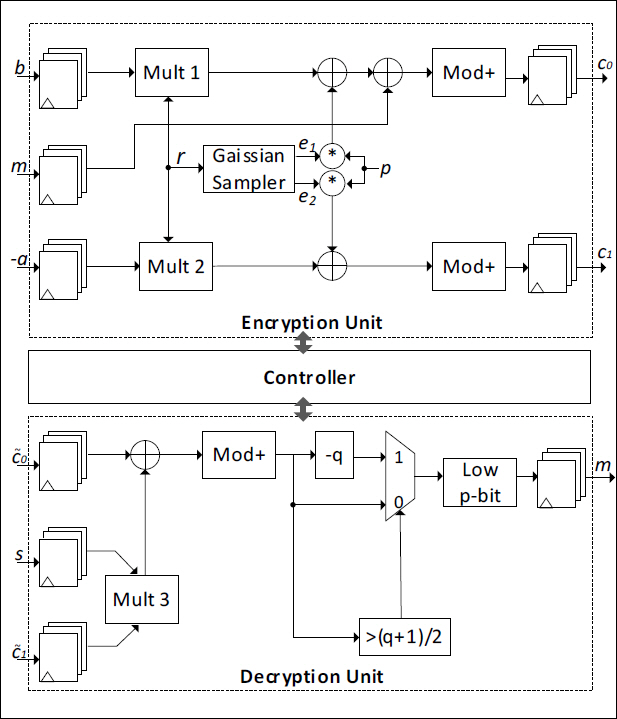
그림 3
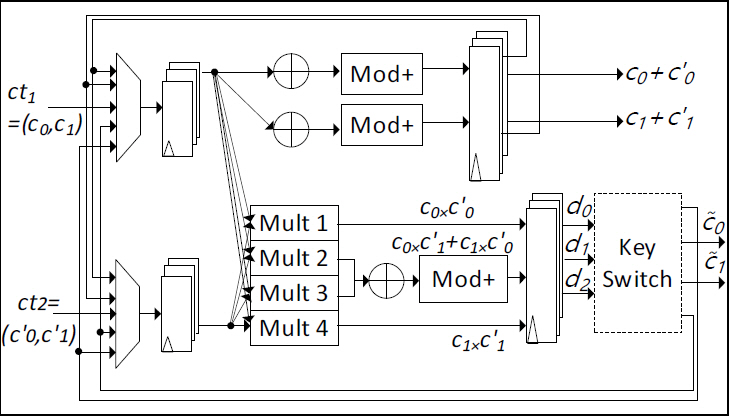
그림 4
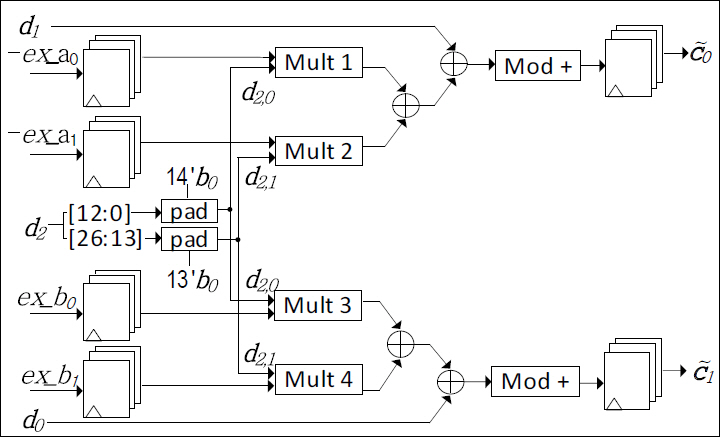
그림 5
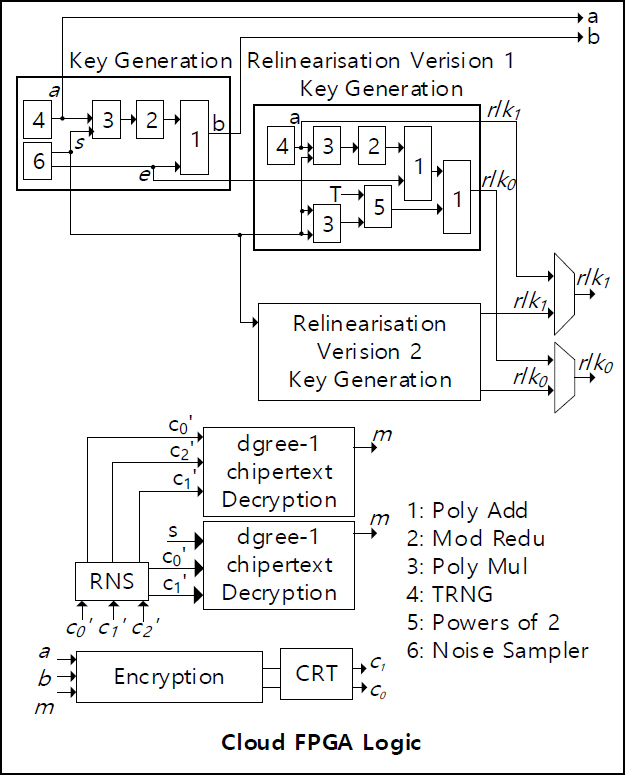
그림 6
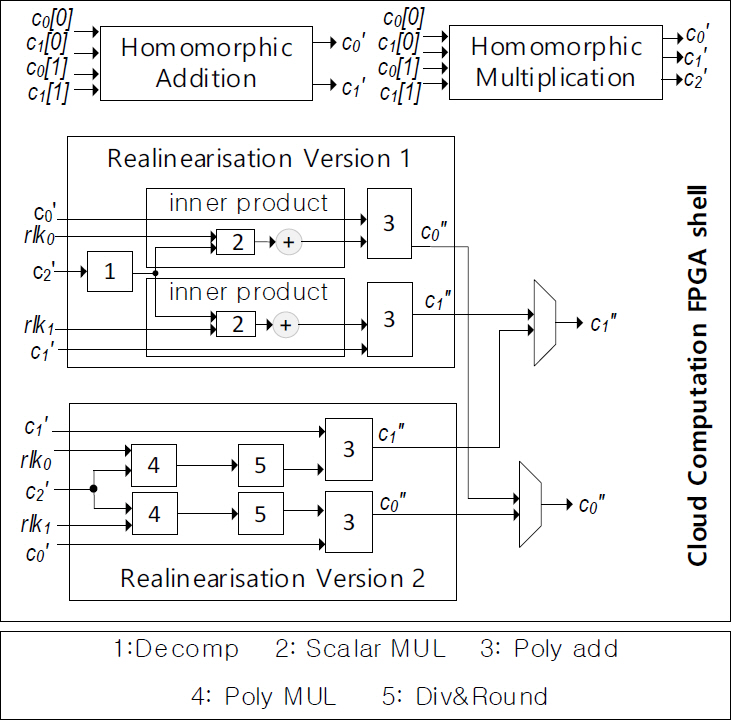
그림 7
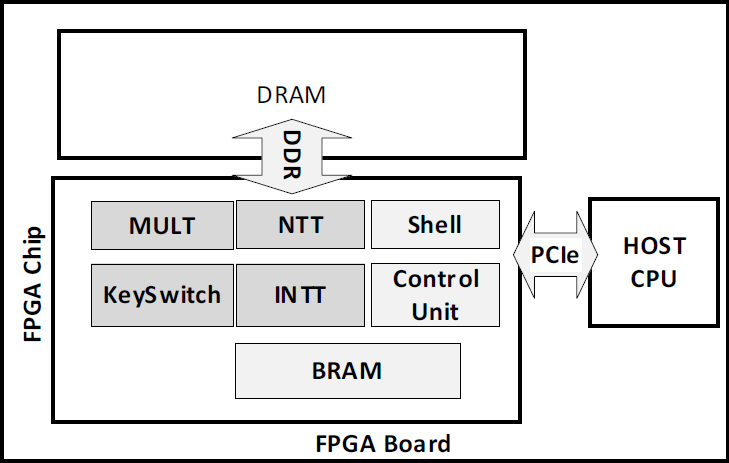
그림 8
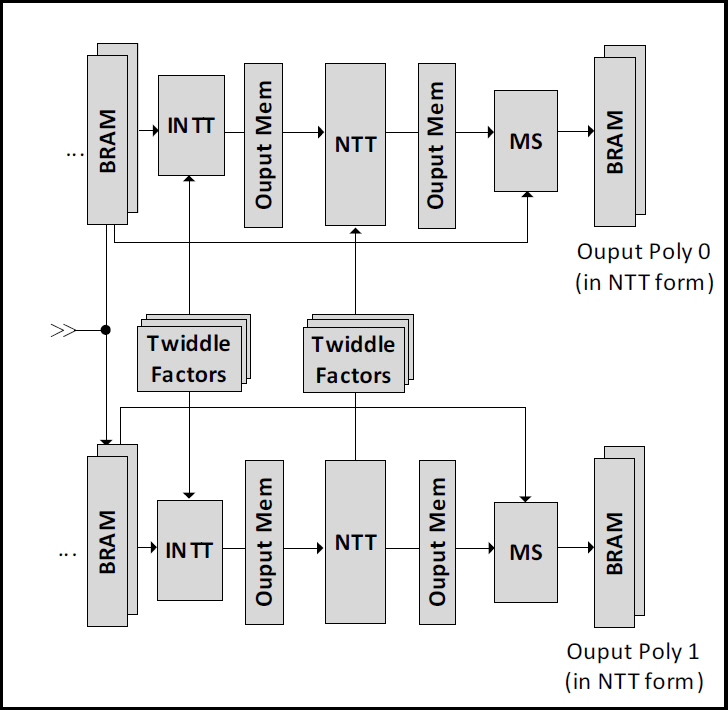
그림 9