NPU 반도체를 위한 저정밀도 데이터 타입 개발 동향
Trends of Low-Precision Processing for AI Processor
- 저자
-
김혜지인공지능프로세서연구실
한진호인공지능프로세서연구실
권영수지능형반도체연구본부
- 권호
- 37권 1호 (통권 194)
- 논문구분
- 인공지능 서비스 및 인프라 기술
- 페이지
- 53-62
- 발행일자
- 2022.02.01
- DOI
- 10.22648/ETRI.2022.J.370106
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- With increasing size of transformer-based neural networks, a light-weight algorithm and efficient AI accelerator has been developed to train these huge networks in practical design time. In this article, we present a survey of state-of-the-art research on the low-precision computational algorithms especially for floating-point formats and their hardware accelerator. We describe the trends by focusing on the work of two leading research groups-IBM and Seoul National University-which have deep knowledge in both AI algorithm and hardware architecture. For the low-precision algorithm, we summarize two efficient floating-point formats (hybrid FP8 and radix-4 FP4) with accuracy-preserving algorithms for training on the main research stream. Moreover, we describe the AI processor architecture supporting the low-bit mixed precision computing unit including the integer engine.
Share
Ⅰ. 서론
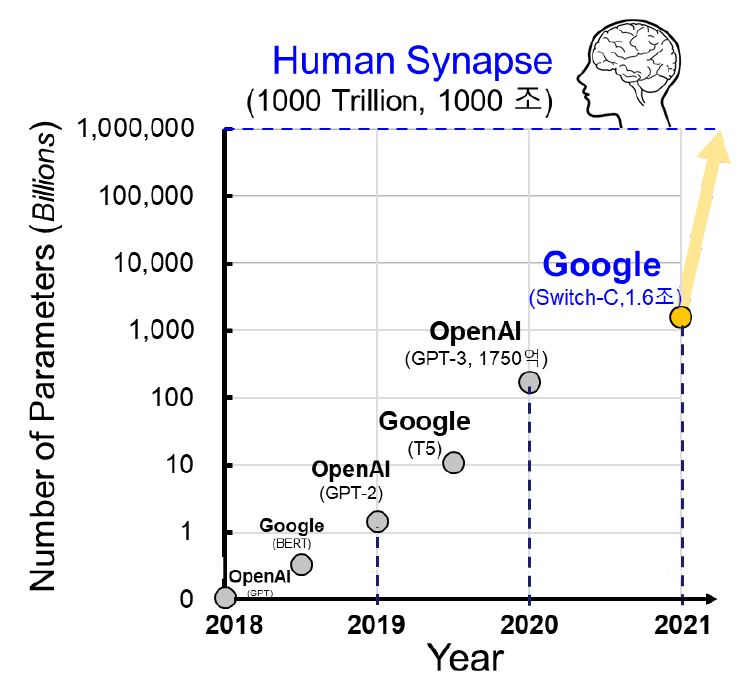
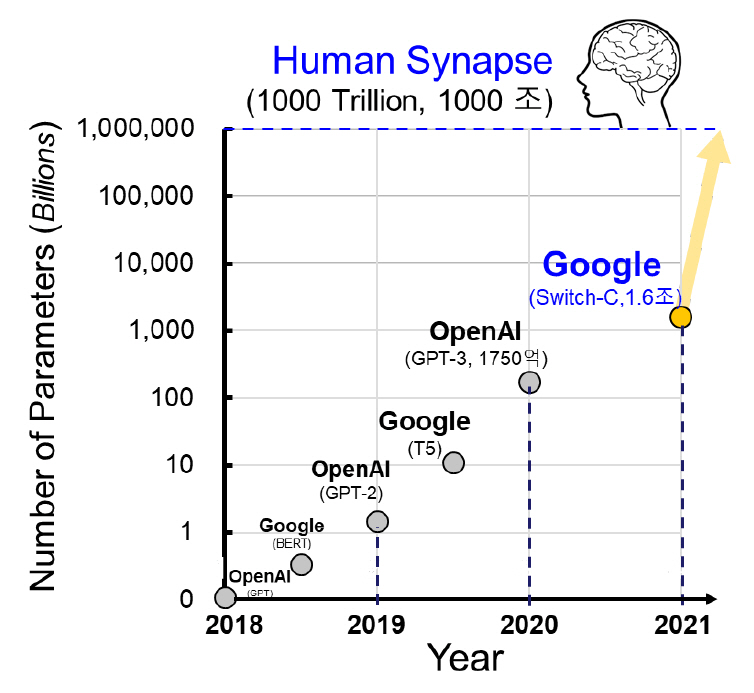
초거대 신경망[1-6]의 등장으로 영상과 언어를 포함한 모든 인공지능 활용분야의 인식 성능이 비약적으로 증가했다. 특히 2018년 OpenAI의 GPT [1] 구조를 시작으로 자연어처리 분야는 무한한 가능성을 맞이하고 있다. 2021년 기준 인공지능 기반 자연어처리 모델의 학습 규모는 1.6조[6]에 육박한다. 이는 매년 10배씩 신경망 구조가 커지고 있으며, 현재와 같은 추세를 따르면 3년 후 초거대 신경망은 사람의 시냅스 수에 도달할 것으로 예상되는 정도다(그림 1 참조). 그뿐만 아니라 영상 처리 분야도 초거대 신경망의 구조를 따라가고 있다. ImageNet 사물 인식 대회의 2021년 기준 상위 3 개의 신경망 모델은 모두 초거대 인공신경망의 핵심 구조(Transformer) [7]를 차용하면서 인식 성능을 경신하는 중이다[8].
이제 신경망의 학습 규모와 관계없이 종국엔 높은 인식 성능으로 잘 학습된 신경망을 만들 수 있다. 신경망은 더욱 전문적이고 구체적인 대답을 하게 될 것이다. 하지만 문제는 하드웨어이다. 잘 만든 신경망이 서비스 수준까지 이어지려면 가능한한 짧은 학습시간과 빠른 처리속도, 그리고 낮은 메모리사용량이 요구된다. 하지만 이 모든 것을 오롯이 하드웨어의 발전에만 맡기기에는 개발 시간과 비용이 많이 든다. 결국 신경망의 경량화 알고리즘 연구가 같이 수반되어야 진정한 고속/저비용 학습 반도체를 구현할 수 있다.
본고에서는 경량화 알고리즘의 한 종류인 양자화를 통한 저정밀 데이터 타입 및 학습 기법의 연구 동향과 이를 지원하는 AI 반도체 연구 동향에 대해 소개한다.
Ⅱ. 저정밀도 학습의 배경
1. 신경망에서의 저정밀도 연산
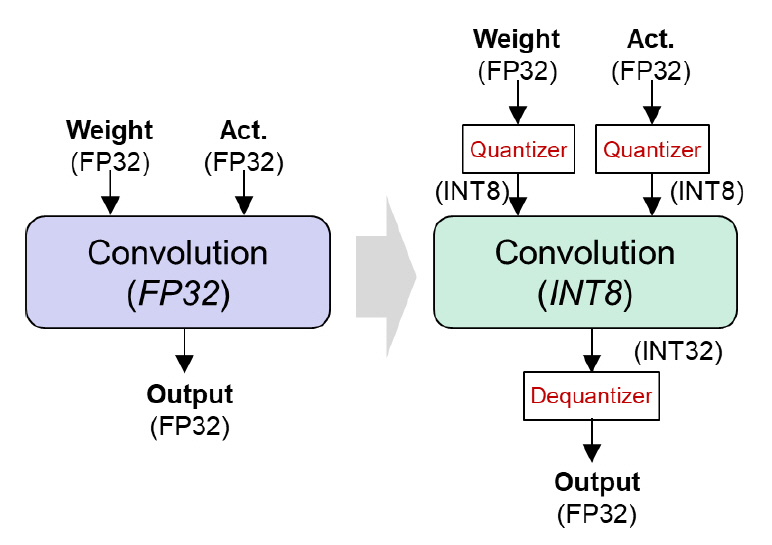
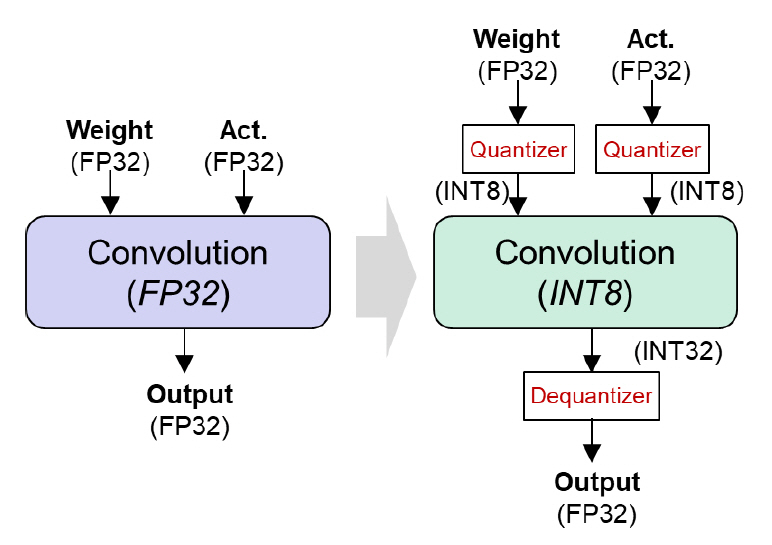
신경망의 경량화 연구는 다양한 방식으로 진행되고 있다. 신경망의 불필요한 파라미터를 제거하는 기법(Pruning), 비슷한 정확도를 내면서 보다 소규모의 신경망 구조로 재학습하는 기법(Knowledge Distillation), 신경망 연산을 저정밀 데이터 타입으로 수행하는 기법(Quantization) 등이 널리 연구되고 있다. 이 중에 가령 GPU와 같은 실제 연산 하드웨어와 직접적으로 연결되는 경량화 기법은 양자화(Quantization)이다. 일반적으로 신경망의 연산함수 입출력에 양자화 모듈을 추가하여 데이터의 포맷을 변환한다. 그리고 전용 연산함수를 호출한 뒤 출력 데이터 타입을 캐스팅하는 방식으로 신경망에 구현된다(그림 2).
양자화 기법의 전제 조건은 하드웨어에 해당 저정밀도 데이터 타입으로 연산 가능한 연산기능이 탑재되어 있어야 한다는 것이다. 또한 이러한 저정밀 데이터 연산기는 기존의 단정밀도(FP32) 연산기보다 월등히 높은 초당 연산량과 낮은 전력사용량 특성을 가져야 한다. 이에 기반하여, NVIDIA A100 GPU의 Tensor Core는 총 5가지의 저정밀도 데이터 연산기를 탑재하고 있다[9]. 부동소수점 연산으로 FP16과 BF16을 지원하고, 정수 연산으로 INT8, INT4, 그리고 Binary 타입을 지원한다. 따라서 양자화 분야를 연구하는 많은 연구자는 INT8 또는 INT4 연산기를 활용하여 제안하는 초저정밀도 양자화 학습 알고리즘을 직접 구현하여 실제 동작속도 및 전력사용량을 확인할 수 있다.
2. 저정밀도 데이터 타입의 개요
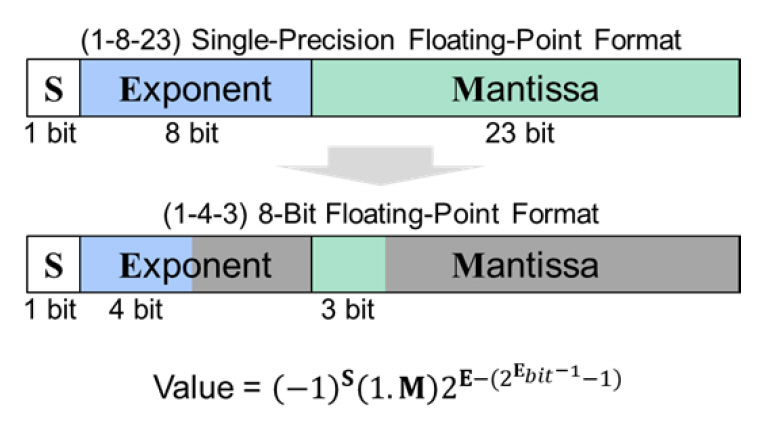
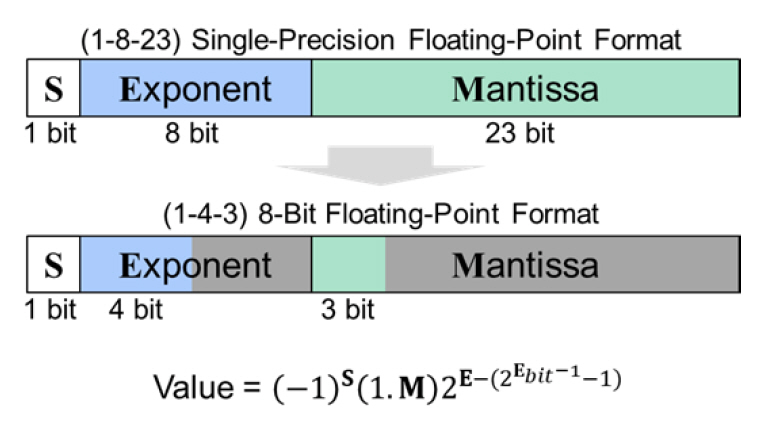
일반적인 신경망 연산에 활용되는 데이터 타입은 부동소수점 기반의 32-bit 단정밀도(FP32) 포맷이다. 그림 3과 같이 부동소수점 포맷은 부호(S), 지수(E), 그리고 가수(M)으로 구성된다. 각 부분이 몇 bit의 크기를 가지는지에 따라 부동소수점 포맷이 결정된다. 본고는 부동소수점 데이터 포맷을 설명할 때 (S-E-M) 형태로 표현한다. 즉 단정밀도의 경우 (1-8-23)이다.
부동소수점 포맷에서 부호는 양수 또는 음수를 표현하며, 지수의 bit 크기는 데이터의 표현범위를 의미한다. 일반적으로 2의 지수값을 포맷에 기재한다. 가수의 bit 크기는 수의 정밀도를 표현하는 데 사용된다. 즉 지수의 할당량이 크고 가수 부분이 작다면, 넓은 범위의 수를 듬성듬성 표현하는 포맷이다. 반대로 지수가 작고 가수가 많이 할당되었다면, 좁은 범위의 수를 미세하게 표현하는 포맷을 의미한다.
Ⅲ. 저정밀도 데이터 타입 기술
1. Hybrid FP8
IBM 연구진은 2018 NeurlPS 학회에서 8-bit 부동소수점 데이터 타입과 정밀도 보상 알고리즘을 제안하여 CNN 계열의 애플리케이션에서 성공적으로 학습할 수 있음을 보였다[10]. 그러나 신경망의 규모가 작아질수록 단일 데이터 타입만으로 정확도 성능을 유지하면서 학습하기에 한계가 있었다. 나아가 추론과 학습 두 가지 상황에서 더욱 안정적인 인식 성능을 달성하기 위해 2019 NeurlPS 학회에서 이종 데이터 타입을 활용한 학습 알고리즘을 제안하였다[11]. 전반적인 학습 연산 패스별 데이터 타입의 종류는 표 1에 정리되어 있다.
표 1 HFP8 연산 패스별 데이터 타입
가. 데이터 타입
신경망의 학습은 입력층에서 출력층으로 전개되는 순방향(Forward-pass) 연산과 출력층에서 입력층으로 전개되는 역방향(Backward-pass) 연산으로 나뉜다. 특히 역방향 연산은 기울기(Gradient)와 손실(Loss)을 연산의 입력으로 사용하며 그 값은 0에 극도로 가깝다. 이러한 특성에 기인하여 8-bit 부동소수점 포맷에서 지수의 가용범위를 넓히고 가수의 정밀도를 낮추는 (1-5-2) 포맷을 사용하고 있다[10].
본 연구는 순방향 연산 데이터의 분포를 보다 세밀하게 관찰했다. 순방향 연산은 가중치(W)와 특징값(A)으로 구성된다. 이 값은 신경망의 계층이 얕을수록 4-bit 지수 범위에 들어오면서 세밀한 데이터의 분포를 보이는 (1-4-3) 포맷에 적합하며, 계층이 깊어질수록 보다 0에 가까운 값들로 구성 되어 (1-5-2) 포맷을 사용해야 양자화에 의한 손실을 줄일 수 있다[11]. 다만, 계층의 깊이에 따라 연산 포맷을 조절하는 것은 부수적인 알고리즘을 요구하게 되어 전체 연산 복잡도를 증가시킨다. 본연구는 넓은 표현범위와 세밀한 정밀도를 모두 만족하기 위해 순방향 연산에서 전역적으로 (1-4-3) 포맷을 사용하면서도 지수에 편향성을 추가하여 상대적으로 큰 값보다 작은 값을 잘 표현하는 비대칭 연산 포맷을 제안하였다.
나. 양자화 손실 보상 기법
행렬 곱은 대표적인 신경망 연산의 한 종류이다. 그 내부는 반복적인 누적 연산으로 구성되어 있다. 신경망의 규모가 커질수록 행렬곱에 의한 누적량은 많아지고 그 결과값은 8-bit로 표현 가능한 범위를 초과할 수 있다. 저정밀도 데이터에서 정보의 손실은 좁은 표현범위와 낮은 정밀도에 기인한다. 본 연구는 행렬 곱 연산에서 낮은 정밀도에 의한 양자화 오차를 극복하는 분할 누적 기법(Chunk-based Accumulation)과 신경망 데이터 분포에 맞게 표현범위를 조절하는 기법(Exponent Bias Shifting)을 제안하였다.
1) Chunk-based Accumulation
누적 연산은 (1-6-9) 포맷을 사용한다. 단정밀도(FP32)는 23-bit의 가수를 활용하는 것과 비교하면 매우 낮은 정밀도로 데이터를 누적한다. 저정밀도 누적에 의한 문제는 부동소수점 덧셈을 할 때 발생한다. 부동소수점 덧셈은 연산자의 지수를 동일하게 맞춘 상태에서 가수 정보를 더하는 방식으로 연산한다. 따라서 한쪽 연산자의 지수 값이 상대적으로 크다면 나머지 연산자는 지수값을 키우고 가수를 낮추는 과정에서 가수 정보를 상당 부분 잃어버리게 된다. 최종적으로 누적된 값은 큰 양자화 오차를 가진다. 이러한 현상을 “swamping”이라 부른다[12].
Swamping은 누적값이 연산 정밀도로 표현 가능한 임계치를 넘거나 순차적인 누적 과정에서 급격히 큰 값이 입력되는 경우 그 현상이 심해진다. 해결 방법은 입력 연산자가 비슷한 범위의 값을 갖게 하여 부동소수점 덧셈을 수행하면 된다. 누적된 값이 임계치를 넘지 않도록 누적 단계를 “chunk” 단위로 분할 연산하는 방식으로 구현하였다. 이는 높은 확률로 swamping에 의한 누적 오차가 커지는 상황을 피할 수 있다.
2) Exponent Bias Shifting
신경망 순방향 연산의 입력 데이터는 전역적으로 (1-4-3) 포맷을 사용한다. 이 경우 신경망의 계층이 깊어질수록 4-bit 지수 정보로는 더 작은 값을 표현하기에 부족하다. 본 연구는 실험적으로 학습 과정에서 깊은 계층의 데이터는 주로 0에 가까운 작은 값들로 구성되므로 상대적으로 큰 값보다 작은 값을 잘 표현할 수 있다면 양자화에 의한 오차를 줄일 수 있음을 확인했다. 따라서 지수에 고정된 편향값 4를 추가하여 기존보다 24배 더 작은 값들을 표현하였다. 이러한 경우 최댓값 또한 24배 줄어들었으나, 학습 데이터는 작은 값 위주로 구성되므로 전체 인식 정확도 성능에 큰 이득을 얻었다.
2. Radix-4 FP4
앞서 소개한 연구를 통해 8-bit 부동소수점 포맷은 신경망을 학습하는 데 충분한 정보량을 가지고 있음을 알 수 있었다. 사실 기존 연구에 따르면 신경망의 추론연산은 정수형 2-bit에서 4-bit 사이의 정보만으로도 정확도의 손실 없이 처리할 수 있다[13-15]. 다만 이러한 초저정밀도 포맷으로 정확도의 손실 없이 신경망을 학습하는 것이 어려웠다. IBM은 2020 NeulPS 학회에서 4-bit의 정보만으로 신경망을 학습할 수 있는 데이터 포맷과 양자화 손실 보상 알고리즘을 제안하였다[16]. 이 방식은 4-bit 정수형 데이터와 새로 제안된 부동소수점 기반의 4-bit 지수형 포맷을 혼합하여 학습한다. 전반적인 학습 연산 패스별 데이터 타입의 종류는 표 2에 정리되어 있다.
표 2 Radix-4 FP4 연산 패스별 데이터 타입
가. 데이터 타입
가중치(W)와 특징값(A)을 4-bit 정수형으로 양자화하며, 그 과정에서 기존에 연구된 기법[13]을 활용하여 양자화 손실을 최소화하였다. 대신 정수형 포맷으로 극복하기 어려웠던 역방향 연산의 기울기 값을 4-bit로 표현하는 새로운 데이터 타입을 제안했다.
예를 들어 CNN 계열의 이미지 분류 네트워크 (ResNet18)를 학습하는 경우, 기울기 값은 2-8에서 26 사이의 분포를 나타낸다[16]. 대부분 데이터는 0에 가까운 값에 집중되어 있으면서도 지수적으로 넓은 가용범위를 요구한다. 이러한 분포도 형태는 정수형 포맷으로 표현하기에 적합하지 않다. 확실한 것은 기울기 값은 지수적으로 넓은 범위에 분포하므로 지수형 데이터 타입을 가져가는 것이 정보 손실을 최소화할 수 있었다. 따라서 본 연구는 부동소수점 기준으로 (1-3-0) 포맷을 사용하여 가수의 정보는 제거하고 지수를 통해 값을 표현한다. 이때, 더욱 넓은 범위의 수를 표현하기 위해 2의 n승을 따르지 않고 4의 n승을 따르는 Radix-4 FP4 포맷을 정의하였다. 이 형태는 Radix-2보다, 그리고 가수 정보가 존재하는 경우보다 월등히 높은 학습 성능을 보이며 단정밀도(FP32) 학습 성능과 거의 유사하다.
나. 양자화 손실 보상 기법
4-bit 포맷으로 표현 가능한 정보는 16개에 지나지 않는다. 이렇게 작은 경우의 수로 데이터를 표현하면서도 단정밀도(FP32)의 학습 성능을 유지하기 위해서는 양자화에 의한 손실을 보상하는 학습 알고리즘이 동반되어야 한다. 본 연구는 데이터의 표현범위를 신경망의 계층마다 별도의 스케일링 펙터로 조절하는 기법(GradScale)과 낮은 정밀도에 의한 양자화 손실을 보상하기 위해 데이터를 서로 다른 방향성으로 근사화하는 기법(Two-phase Rounding)을 제안하였다.
1) GradScale
스케일링은 입력 데이터를 저정밀도 포맷의 가용범위로 이동하는 기법이다. 특히 데이터 포맷의 bit 수가 작아질수록 표현범위는 상당히 제한적이므로 적절한 데이터 스케일링 펙터를 정의하는 것은 매우 중요하다.
실험적으로 모든 신경망 계층에 공통으로 하나의 스케일링 펙터를 사용하는 것은 4-bit 포맷에 적합하지 않았다. 다양한 계층의 데이터에 대해 공통된 단일 스케일링 펙터를 정의하는 것은 학습 성능 저하를 야기한다. 이를 해결하기 위해 스케일링 펙터를 각 계층의 학습 파라미터로 추가하여, 신경망이 학습되는 동시에 연산 데이터를 4-bit 범위로 표현하는 최적의 스케일링 펙터 또한 동시에 계산한다. 이는 신경망의 학습과 스케일링 펙터의 최적화 과정을 통합하여 추가적인 보상 알고리즘을 간략화하였다.
2) Two-phase Rounding
Radix-4는 4의 n승으로 수를 표현한다. 기존 부동소수점의 지수는 2의 배수인 것에 비해 4의 배수는 그보다 2배 더 커서 데이터 표현범위는 넓지만, 연산 정밀도가 2배 낮아진다. 본 연구는 radix-4 체계를 짝수형과 홀수형으로 나누어 서로 다른 방향으로 근사화를 수행하도록 하였다. Radix-4는 다르게 보면 radix-2 체계에서 짝수만 존재하는 경우로 해석할 수 있다. 여기서 가상으로 홀수도 존재한다고 생각하면 임의의 수를 radix-4 짝수형과 홀수형, 두 가지 수체계로 확장할 수 있다. 이는 마치 연산 정밀도를 2배 높이는 것과 같은 효과를 얻는다. 근사화의 기준점은 데이터 간격의 중간값이 아닌 4의 n승 체계에 근거하여 1.6배를 중심으로 값을 올리거나 내림한다.
신경망 학습 과정에서 손실 기울기는 가중치 기울기를 구하면서 특징값 기울기를 구하는 목적으로 동시에 사용된다. 따라서 하나의 손실 기울기를 서로 다른 차원의 수체계로 할당하여 각각 근사화 기법을 적용한 별도의 연산을 수행하면, 최종적으로 보다 양자화 손실이 감소된 학습 결과를 얻을 수 있다.
Ⅳ. 저정밀도 연산 AI 반도체 기술
저정밀도 연산의 궁극적인 목표는 신경망의 추론 및 학습 시간을 단축하고 메모리 사용량과 에너지 소모량을 감소하는 데 있다. 실제 동작 환경에서 자원과 시간의 이득을 얻기 위해선 저정밀도 알고리즘 개발과 더불어 AI 반도체 기술 연구가 동반되어야 한다. 저정밀도 AI 반도체는 낮은 복잡도의 연산기를 고집적 설계하여 높은 병렬성을 이용해 초당 연산량을 극대화하는 것이 특징이다. 이를 위하여 고대역폭 데이터 전송기술, 메모리와 연산기의 효율적인 구조 기술, 그리고 저전력 연산을 위한 전력 제어기술이 연구되고 있다.
1. IBM RaPiD
IBM은 2021 ISSCC [17]와 ISCA [18] 학회에서 8-bit 부동소수점 기반의 이종 데이터 타입으로 신경망을 학습하고 4-bit 이하의 정수형 데이터 타입으로 추론연산을 수행하는 AI 반도체(RaPiD)를 공개하였다. 데이터 타입의 타당성과 저정밀도 타입의 학습 알고리즘은 앞선 연구[11]를 근거로 제안되었다.
가. AI 반도체 구조
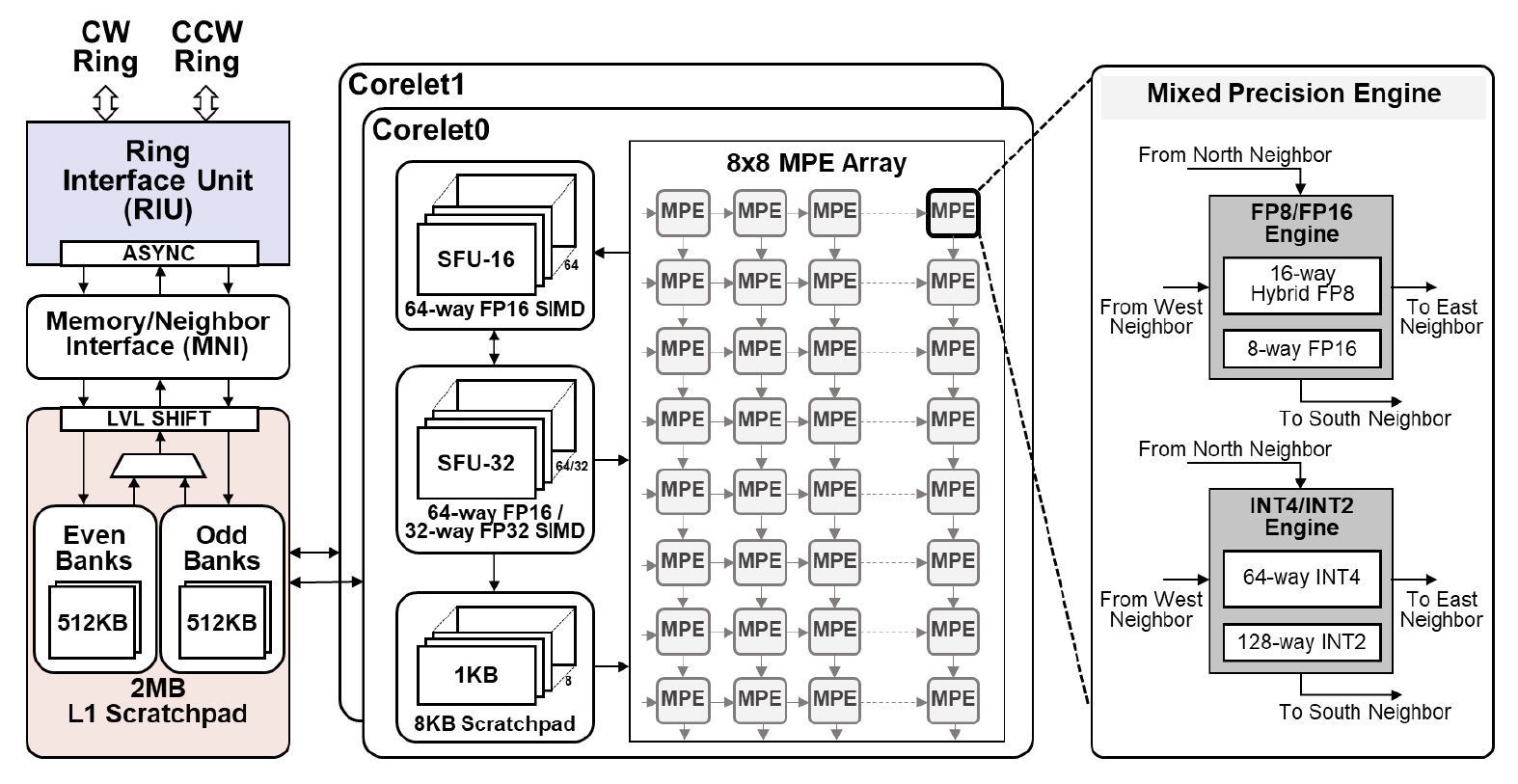
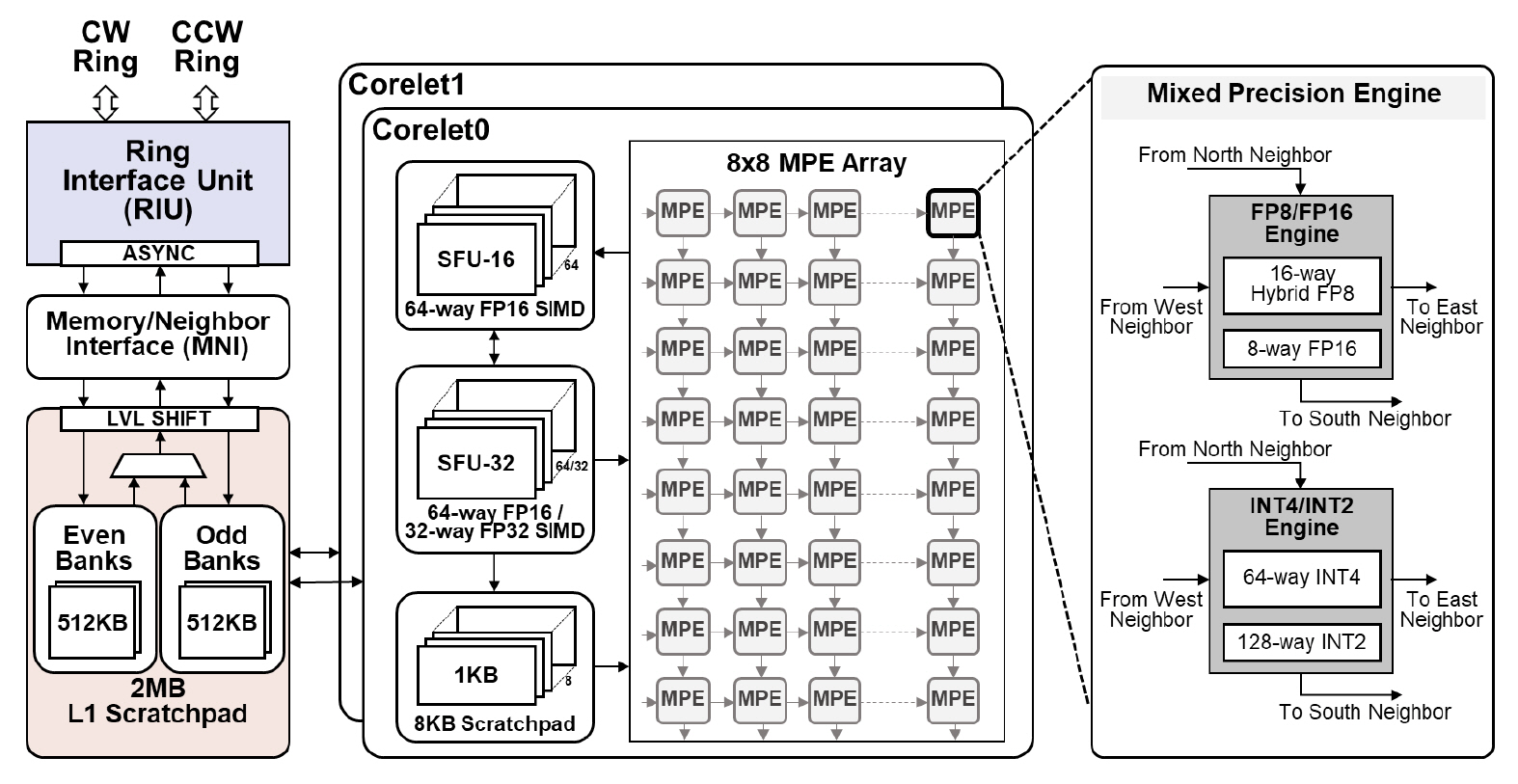
RaPiD는 칩당 4개의 저정밀도 연산 코어가 양방향(Bi-directional) 이중 링버스로 연결되어 있다. 이러한 구조는 코어 또는 칩의 개수를 확장하여 연산 성능을 조절하는 데 적합하다. 두 개의 링버스와 연산 코어는 비동기(Asynchronous) 클락 도메인에서 동작하며 각각 별도의 위상동기회로(PLL)를 가진다. 링버스는 클락 사이클당 128바이트의 데이터를 전송하여 고대역폭 환경을 제공한다.
1) Core
Core는 저정밀도 데이터 타입을 지원하는 2개의 Corelet과 모든 연산모듈이 공유하는 2MB L1 메모리(Scratchpad), 메모리 간 데이터 이동과 링버스로 데이터 전송을 제어하는 인터페이스(MNI), 그리고 양방향 이중 링버스에 비동기 도메인으로 연결되어 링버스와의 데이터 전송을 제어하는 인터 페이스 유닛(RIU)으로 구성된다(그림 4). 링버스에 의한 전송 지연시간 완화를 위해 L1 메모리는 이중 버퍼링 구조를 사용하였다.
2) Corelet
Corelet은 8 × 8 구조의 시스톨릭 기반 복합 데이터 타입 연산 어레이(MPE Array), 비선형 함수 연산 유닛(SFU), 그리고 8KB L0 메모리(Scratchpad)로 구성되어 있다(그림 4). 시스톨릭 기반 MPE 어레이는 행렬연산을 가속하는 데 활용되며, SFU는 신경망의 특징값 계산용 비선형 함수를 비롯하여 정규화, 풀링 등 다양한 함수 계산에 사용된다. 각 연산기에서 지원하는 저정밀도 데이터 타입은 표 3에 정리되어 있다.
표 3 Corelet 연산기에서 지원하는 데이터 타입
| 연산기 | 입력 데이터 타입 |
|---|---|
| MPE | 정수형(INT4, INT2) |
| 부동소수점형(DLFloat16, HFP8) | |
| *DLFloat16: (1-6-9) | |
| *HFP8: fw(1-4-3)&bw(1-5-2) | |
| SFU | 부동소수점형(FP32, DLFloat16) |
| *FP32: (1-8-23) | |
| *DLFloat16: (1-6-9) |
8 × 8 MPE 어레이는 MPE마다 16바이트의 행과열 방향 데이터를 각각 L0와 L1 메모리에서 공급 받는다. 따라서 MPE 내부의 연산기는 8-bit 부동 소수점 연산에서 동시에 16개 데이터를 처리한다. SFU모듈은 총 MPE 어레이의 출력과 직접 연결되어 사이클당 128바이트 정보를 처리한다. 16-bit 부동소수점의 경우 64개 데이터를 병렬로 처리함을 의미한다.
3) Mixed Precision Engine
MPE는 정수형 연산과 부동소수점 연산을 지원한다. 특히 RaPiD는 신경망 학습에서 순방향과 역방향에서 서로 다른 8-bit 부동소수점 포맷을 사용 한다. 연산기 내부에서 모든 포맷을 지원하기 위해 별도의 연산기를 두는 것은 부수적인 하드웨어 자원을 요구한다. 본 연구는 내부적으로 통합형 포맷(1-5-3)으로 변환하여 MAC연산을 수행한다. 즉 실제 메모리에는 8-bit 데이터를 저장하되, 연산기 내부에서 9-bit 포맷으로 자동 변환하여 사용한다. 내부적으로 덧셈 연산은 16-bit를 포맷을 사용한다. 따라서 입력 bit 수에 관계없이 최종적으로 16-bit 부동소수점 데이터를 출력한다.
2. Seoul National University
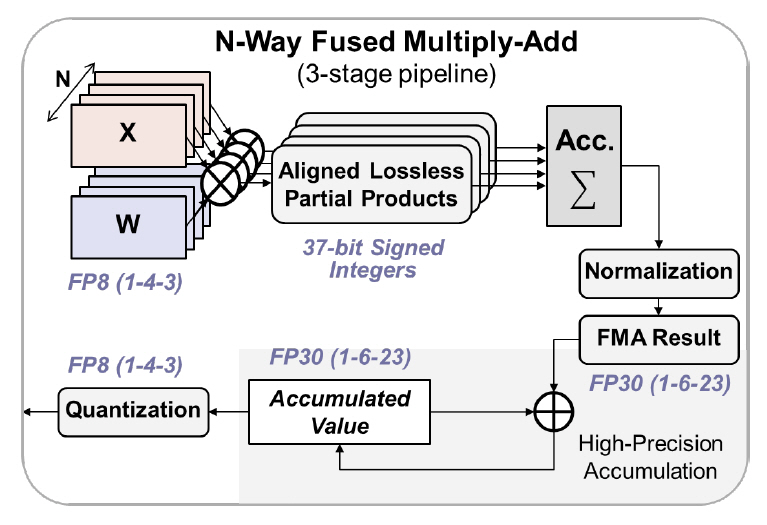
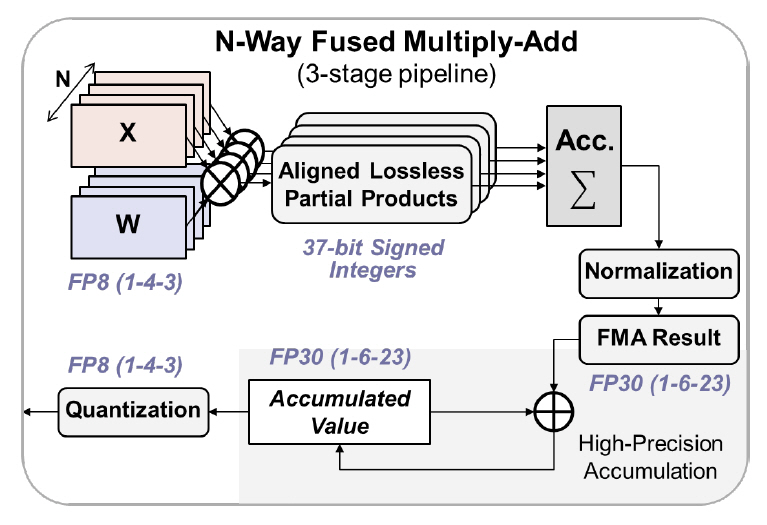
서울대학교 연구진은 2021 ISSCC 학회에서 마찬가지로 8-bit 부동소수점 포맷을 사용한 학습용 AI 반도체를 공개하였다(그림 5) [19]. 저정밀도 연산기 면에서 IBM 연구와의 차이점은, 전체 신경망 연산에서 한 가지 8-bit 데이터 타입만 사용한다는 것이다. 서울대는 부동소수점 (1-4-3) 포맷을 선택했다.
기존 저정밀도 학습 알고리즘의 연구 결과에 따르면, (1-4-3) 포맷은 학습용 역방향 연산에서 기울기 정보를 표현하기에는 지수의 가용범위가 부족하다[11]. 본 연구는, 이 문제를 해결하기 위해 8-bit 포맷에 지수 편향정보를 추가했다. 각 입력 텐서(Tensor)에 공통으로 적용되는 지수 편향 값을 학습 과정에서 추적하여, 연산기에 실시간으로 반영한다. 해당 기법을 활용하면 단일 포맷으로 신경망 학습 연산이 가능하여 연산기를 보다 간단하게 구현할 수 있다.
가. 저정밀도 연산기 구조
연산기는 24개의 8-bit 입력 세트를 동시에 처리하는 24-way 구조를 지원한다. 특히 저정밀도 데이터 누적에 의한 “swamping” [12] 현상을 방지하기 위해 누적 연산은 총 2단계로 나누었다. 1단계는 24세트 데이터를 무손실 정수형으로 변환하여 곱셈을 수행한 후 덧셈을 Tree 구조로 구현하였다. 이어서 단정밀도(FP32)를 간략화한 FP30(1-6-23) 포맷을 새로 정의하여 2단계 누적 연산에 사용하였다. 최종 결과는 입력과 같은 8-bit 부동소수점 포맷으로 양자화하여 출력한다. 최종적으로 단일 8-bit 포맷에 지수편향 기법을 적용하고 FP30 포맷으로 이중 누적하는 연산기 구조는 8-bit/16-bit 포맷의 혼합 구조[20]보다 약 43% 메모리 접근이 감소한다. 또한 학습 정확도 성능은 단정밀도 (FP32)와 근사함을 실험적으로 보였다.
Ⅴ. 결론 및 맺음말
이제 인공신경망은 부동소수점 4-bit로 충분히 학습 가능하다. 즉 단정밀도 대비 학습 파라미터의 메모리 저장용량만 단순 계산해도 1/8로 감소하였다. 더불어 저정밀도 연산 기능이 탑재된 AI 반도체는 성공적으로 연구되고 있다. 연산기는 행렬곱 연산에 최적화되어 초당 연산량이 급격히 증가하였다. 따라서 앞으로 행렬연산은 더 이상 신경망의 최대 병목 부분이 아닐 수 있음을 시사한다.
양자화와 관련된 향후 연구는 새로운 수 체계를 정의하는 데에 있다고 예상한다. 최근 연구에서 부동소수점 4-bit 포맷은 가수가 사라지고 지수만 남았다. 심지어 2의 승수가 아닌 4의 승수다. 이는 기존의 부동소수점 포맷을 벗어나서 보다 학습에 적합한 새로운 데이터 표현구조가 존재할 수 있음을 의미한다. 실제로 posit을 이용한 연구[21]가 진행 되고 있는 것도 같은 의미이다. 이러한 복합 데이터 타입을 AI 반도체에서 낮은 복잡도로 구현하여 집적도를 최대화하는 기법, 다양한 데이터 타입의 변환 과정에서 불필요한 지연시간을 최소화하는 기법, 그리고 고집적 고속연산 구조에서 최대 대역폭으로 데이터를 전송하는 기법 등의 연구가 성숙되어 AI 반도체의 혁신을 이루길 기대한다.
용어해설
Scratchpad 프로세서 연산 과정의 데이터를 저장하는 고속 내부 메모리 구조
약어 정리
A. Radford et al., "Improving language understanding by generative pre-training," OpenAI Blog, 2018.
J. Devlin et al., "Bert: Pre-training of deep bidirectional transformers for language understanding," arXiv preprint, CoRR, 2018, arXiv: 1810.04805.
C. Raffel et al., "Exploring the limits of transfer learning with a unified text-to-text transformer," arXiv preprint, CoRR, 2019, arXiv: 1910.10683.
T.B. Brown et al., "Language models are few-shot learners," arXiv preprint, CoRR, 2020, arXiv: 2005.14165.
W. Fedus, B. Zoph, and N. Shazeer, "Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity," arXiv preprint, CoRR, 2021, arXiv:2101.03961.
A. Vaswani et al., "Attention is all you need," in Proc. Conf. Neural Inf. Process. Syst., (Long Beach, CA, USA), Dec. 2017, pp. 5998-6008.
N. Wang et al., "Training deep neural networks with 8-bit floating point numbers," in Proc. Int. Conf. Neural Inf. Proc. Syst., (Montreal, Canada), Dec. 2018, pp. 7686-7695.
X. Sun et al., "Hybrid 8-bit floating point (HFP8) training and inference for deep neural networks," in Proc. Int. Conf. Neural Inf. Proc. Syst., (Vancouver, Canada), Dec. 2019, pp. 4900-4909.
N.J. Higham, "The accuracy of floating point summation," SIAM J. Sci. Comput., vol. 14, no. 4, 1993, pp. 783-799.
J. Choi et al., "Pact: Parameterized clipping activation for quantized neural networks," arXiv preprint, CoRR, 2018, arXiv: 1805.06085.
S.K. Esser et al., "Learned Step Size Quantization," in Proc. Int. Conf. Learn. Represent., (Addis Ababa, Ethiopia), Feb. 2020.
D. Zhang et al., "Lq-nets: Learned quantization for highly accurate and compact deep neural networks," in Proc. Eur. Conf. Comput. Vis. (ECCV), (Munich, Germany), Sept. 2018, pp. 365-382.
X. Sun et al., "Ultra-low precision 4-bit training of deep neural networks," in Proc. Conf. Neural Inf. Process. Syst., (Vancouver, Canada), Dec. 2020.
A. Agrawal et al., "A 7nm 4-core AI chip with 25.6 TFLOPS hybrid FP8 training, 102.4 TOPS INT4 inference and workload-aware throttling," in Proc. IEEE Int. Solid-State Circuits Conf. (ISSCC), (San Francisco, CA, USA), Feb. 2021, pp. 144-146.
S. Venkataramani et al., "RaPiD: AI accelerator for ultra-low precision training and inference," in Proc. ACM/IEEE Annu. Int. Symp. Comput. Archit. (ISCA), (Valencia, Spain), June 2021, pp. 153-166.
J. Park, S. Lee, and D. Jeon, "A 40nm 4.81 TFLOPS/W 8b floating-point training processor for non-sparse neural networks using shared exponent bias and 24-way fused multiply-add tree," in Proc. IEEE Int. Solid-State Circuits Conf. (ISSCC), (San Francisco, CA, USA), Feb. 2021, pp. 1-3.
J. Lee et al., "LNPU: A 25.3 TFLOPS/W sparse deep-neural-network learning processor with fine-grained mixed precision of FP8-FP16," in Proc. IEEE Int. Solid-State Circuits Conf. (ISSCC), (San Francisco, CA, USA), Feb. 2019, pp. 142-144.
표 1 HFP8 연산 패스별 데이터 타입
출처 Reproduced from [11].
표 2 Radix-4 FP4 연산 패스별 데이터 타입
출처 Reproduced from [16].
표 3 Corelet 연산기에서 지원하는 데이터 타입
| 연산기 | 입력 데이터 타입 |
|---|---|
| MPE | 정수형(INT4, INT2) |
| 부동소수점형(DLFloat16, HFP8) | |
| *DLFloat16: (1-6-9) | |
| *HFP8: fw(1-4-3)&bw(1-5-2) | |
| SFU | 부동소수점형(FP32, DLFloat16) |
| *FP32: (1-8-23) | |
| *DLFloat16: (1-6-9) |
출처 Reproduced from [17].
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.