결함허용 양자컴퓨팅 시스템 기술 연구개발 동향
Technology Trends of Fault-tolerant Quantum Computing
- 저자
-
황용수양자컴퓨팅연구실
김태완양자컴퓨팅연구실
백충헌양자컴퓨팅연구실
조성운양자컴퓨팅연구실
김홍석양자컴퓨팅연구실
최병수양자컴퓨팅연구실
- 권호
- 37권 2호 (통권 195)
- 논문구분
- ICT 창의연구, 양자에서 우주까지
- 페이지
- 1-10
- 발행일자
- 2022.04.04
- DOI
- 10.22648/ETRI.2022.J.370201
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- Similar to present computers, quantum computers comprise quantum bits (qubits) and an operating system. However, because the quantum states are fragile, we need to correct quantum errors using entangled physical qubits with quantum error correction (QEC) codes. The combination of entangled physical qubits with a QEC protocol and its computational model are called a logical qubit and fault-tolerant quantum computation, respectively. Thus, QEC is the heart of fault-tolerant quantum computing and overcomes the limitations of noisy intermediate-scale quantum computing. Therefore, in this study, we briefly survey the status of QEC codes and the physical implementation of logical qubit over various qubit technologies. In summary, we emphasize 1) the error threshold value of a quantum system depends on the configurations and 2) therefore, we cannot set only any specific theoretical and/or physical experiment suggestion.
Share
Ⅰ. 서론
양자컴퓨터는 양자 역학적 현상을 적용하여 다수의 정보를 병렬 연산을 통해 처리하기 때문에 기존 컴퓨터를 월등히 뛰어넘는 연산 처리 능력을 가지고 있다. 따라서 양자컴퓨팅은 빅데이터, AI, 암호 등에 적용하여 의료, 금융, 물류, 항공우주, IT 등 방대한 데이터 처리를 요구하는 사회 전 분야에 활용할 수 있어 본격적으로 4차 산업혁명을 이끌 수 있는 핵심기술로서 그 파급력은 크다고 할 수 있다.
양자컴퓨팅에서 가장 기본적인 연산인 유니타리(Unitary) 양자 게이트를 정확하게 수행하기 위해서는 큐비트의 결맞음(Coherence) 시간과 게이트의 신뢰도(Fidelity)가 중요하다. 기본적으로 큐비트는 물리 시스템이므로 결맞음 시간과 게이트 신뢰도를 무한히 향상시키더라도 큐비트 제어과정에서 오류가 발생할 가능성은 항상 존재한다. 실생활 난제를 해결하는 양자 알고리즘(예: 소인수분해, 데이터 검색, 시뮬레이션 등)은 크기(큐비트 수, 알고리즘 길이)가 매우 크기 때문에, 해당 알고리즘을 높은 신뢰도로 실행하기 위해서는 큐비트와 게이트의 신뢰도가 매우 높아야 한다. 현재까지 개발된 큐비트의 성능은 물론이고, 향후 새로운 큐비트가 개발될지라도, 그 성능은 현 양자 알고리즘을 직접적으로 수행할 수 있을 정도(10-20~10-15 수준 오류율)가 되기는 어려울 것으로 예상된다.
이러한 문제점을 해결 및 보완하기 위해서 고전적으로 많이 사용되는 오류보정 방식을 양자정보에 적용하는 방법이 제안되었다[1]. 이는 1개의 물리 큐비트에 저장된 논리적 데이터를 N개의 물리 큐비트(Codeword)에 분배하여, 임의의 큐비트에 오류가 발생하더라도, 나머지 큐비트가 가지고 있는 정보들을 기반으로 원래의 데이터를 복원하는 방식으로 양자오류보정(Quantum Error Correction)이라고 부른다.
양자오류보정은 부호화(Encoding) 과정을 통해서 1개의 물리 큐비트가 가지고 있던 양자정보 데이터를 N개의 물리 큐비트가 나누어 가지게 되는데, 이 N개가 얽힌 물리 큐비트 묶음을 오류보정된 논리 큐비트(Error-Corrected Logical Qubit)라고 부른다(이하 ‘논리 큐비트’라고 함). 양자오류보정이 정확하게 동작하게 되면, 논리 큐비트는 물리 큐비트가 가지는 결맞음 시간을 능가하는 논리적 결맞음 시간을 가지게 된다. 즉, 양자정보 데이터를 물리 큐비트에 저장하는 것보다 논리 큐비트에 저장하는 것이 더 오랜 시간 유지된다는 의미이다.
양자정보를 논리 큐비트에 저장하고 주기적으로 양자오류보정을 인가함으로써 임의의 오랜 시간 동안 유지하는 것에 더해, 논리 큐비트에 저장된 양자 상태를 조작하기 위해 논리 큐비트 맞춤형 논리 게이트를 구현할 수 있다. 그리고 논리 큐비트에 논리 게이트를 인가한 이후/또는 인가하는 중간에 양자 오류보정을 적용하여, 물리 게이트의 신뢰도를 능가하는 논리 게이트 구현이 가능하고, 따라서 물리 큐비트/게이트 대비 고신뢰도의 논리 큐비트/게이트 기반 양자컴퓨팅이 가능하다. 그 결과 실생활 난제를 풀어낼 수 있는 수준의 양자컴퓨팅이 가능해진다.
이러한 양자오류보정이 적용된 양자컴퓨팅을 결함허용 양자컴퓨팅(FTQC: Fault-Tolerant Quantum Computing)이라고 부르는데, 이는 논리 큐비트로 연산하는 양자컴퓨팅 기술로 모든 알고리즘에 활용할 수 있으며 빅데이터, 머신러닝 및 암호체계 분야 등에 혁신적인 변화를 가져올 수 있다. 그러나, 세계적으로 현재의 기술 수준이 높지 않아 기술 성숙이 더욱 요구되고 있다. 또한, 논리 큐비트를 만들 수 있을 만큼 물리 큐비트의 에러율이 충분히 낮아야 하며, 여러 개의 물리 큐비트가 필요하여 확장성과도 연계되어 있어 높은 기술 수준을 요구하고 있다. 그리고 이를 실제로 구현하기 위해서는 부호화, 복호화 등의 과정에서 오류가 발생하더라도 논리 큐비트의 오류보정이 가능하도록 설계해야 하며 이를 결함허용적 설계라고 한다[2].
실제로 작동하는 결함허용 양자컴퓨팅 구현을 위해서는 컴파일러, 합성기, 운영체제, 결함허용 처리기, 제어기 및 논리 큐비트 등 여러 계층적 구조와 구성기술들이 결함허용적 설계에 따라 최적화되어 구현되어야 한다. 따라서 본고에서는 결함허용적 설계 관점에서 진행되고 있는 결함허용 양자컴퓨팅 연구개발의 전반적인 내용 및 구체적인 연구개발 동향과 향후 연구개발 이슈들에 대해서 살펴보고자 한다.
II. 결함허용 양자컴퓨팅 구성요소
결함허용 양자컴퓨팅은 오류보정 소프트웨어 기술로 하드웨어에 발생하는 양자오류를 억제하면서 알고리즘을 수행하는 기술이다. 오류보정 소프트웨어 기술을 적용하여 다수의 물리 큐비트를 얽힘 상태(논리 큐비트)로 만들고, 물리 큐비트에 발생한 양자오류가 전체 양자컴퓨팅 수행에 영향을 미치는 것을 최대한 억제한다.
오류보정 소프트웨어 기술은 양자오류보정 관점에서 크게 오류보정이 적용된 논리 큐비트 구동 파트와 논리 큐비트 구동 지원 파트로 구성된다. 논리 큐비트 구동 파트는 물리 큐비트에 발생한 오류를 탐지(Syndrome Measure), 복호화(Decoding) 및 수정(Recovery)하는 양자오류보정과 논리 큐비트의 양자 상태를 초기화(Preparation), 조작(Manipulation) 및 측정(Measurement)하는 논리 게이트(Logical Gate)로 구성된다. 오류보정과 논리 게이트의 구체적인 프로토콜은 양자오류보정부호에 의해 정의된다.
논리 큐비트 구동 지원 파트는 논리 큐비트 구동 파트가 원활하게 수행될 수 있도록 하는 양자컴퓨팅 구성요소들을 지칭한다. 예를 들어, 논리적 수준의 양자 컴파일은 사용자가 작성한 양자 알고리즘이 결함허용적으로 구동되는 데 매우 필수적인 요소이다. 양자 알고리즘은 큐비트의 위상각(θ)에 대한 회전 게이트(Rz(θ))가 포함될 수 있는데, 이론적으로 임의각도에 대한 회전 게이트를 결함허용적으로 구현하는 것은 매우 어렵다. 따라서 일반적인 접근법은 해당 게이트를 결함허용적으로 구현 가능한 게이트들의 조합으로 분해하는 것인데, 이를 수행하는 양자컴퓨팅 구성요소가 논리적 수준의 양자 컴파일이다[3,4]. 또한, 양자오류보정 부호에 따라 구현 가능한 횡단(Transversal)게이트1) 형태의 결함허용 논리 게이트가 다르기 때문에[5], 사용자가 작성한 양자 알고리즘을 양자오류보정부호에 따라 다르게 분해할 필요가 있다.
이외에도 양자 알고리즘의 흐름에 따라 논리 큐비트의 상위 계층에서 논리 큐비트/게이트의 구동을 관리하는 시스템 수준에서의 논리 큐비트 제어 및 관리 기술과 논리 큐비트 수준에서 물리 큐비트/게이트의 오류보정을 위한 구동을 관리하는 개별 논리 큐비트 수준에서 물리 큐비트 제어 및 관리 기술은 결함허용 양자컴퓨팅을 효과적으로 수행하는 데 필수적인 요소들이다.
물리적 양자컴퓨팅 하드웨어는 근본적으로 일정 정도의 노이즈를 가지고 있기 때문에 양자오류보정을 실행하는 과정 중에도 양자오류는 지속적으로 발생하고, 논리 큐비트에 오류가 누적될 수 있다. 당연히, 누적된 오류의 양이 양자오류보정부호의 오류보정 능력을 벗어나면, 오류보정이 정확하게 수행될 수 없다. 따라서, 양자오류보정이 성공적으로 오류제어를 할 수 있는 양자오류 가능 영역이 존재한다. 이를 나타내는 것이 Accuracy Threshold 법칙[6]으로 임계 오류율 이하의 양자오류가 발생하면, 양자오류보정이 성공적으로 오류를 제어할 수 있다. 임계 오류율은 양자오류보정부호, 오류 복호화 알고리즘, 결함허용 양자컴퓨팅 프로토콜 등 다양한 요소들에 의해 결정된다. 결함허용 양자컴퓨팅 수행에 요구되는 오류 임계값은 규모가 가장 큰 CNOT 게이트 프로토콜을 기준으로 계산한다[6].
다음에서 살펴보겠지만, 연접(Concatenated) 양자 부호의 경우, 오류 임계값이 10-5 이하 정도로 보고되고 있고, 위상학적 양자부호는 상대적으로 높은 10-3~10-2 수준이다. 하지만, 이러한 수치들은 실생활 난제 해결에 요구되는 큐비트의 오류율 10-15 이하 수준과는 그 차이가 큰데, 그 간극을 concatenation level을 높이거나(Concatenated Code) 또는 code distance(위상학적 부호)를 높이는 것으로 메우고 있다.
앞서 언급한 바와 같이 Accuracy Threshold 등 결함허용 양자컴퓨팅의 이론적 성능을 결정하는 것은 양자오류보정부호(복호화 알고리즘 포함) 및 관련 결함허용 프로토콜이다. 범용 결함허용 양자컴퓨팅 실현을 위해서 그동안 다양한 연구개발이 진행되어 왔는데, 본고에서는 대표적인 양자오류보정부호에 대해서만 살펴보도록 한다.
비트 오류 (| 0 >↔| 1 >) 와 위상오류(a|0>+b|1>↔a|0>-b|1>)가 동시에 발생하는 양자 오류로부터 양자정보를 보호하기 위해, 양자컴퓨팅 연구개발 초기 단계에서는 기존 디지털 통신에서 활용되고 있는 고전 선형부호가 적용되었다. ((9,1,3)) Shor 부호[7]의 경우 3-큐비트 반복 부호를 적용한 것이고, ((7,1,3)) Steane code[8] 경우 (7,4,3) Hamming 부호를 적용하여 개발한 부호이다. 그 외에도 선형부호에서 잘 알려져 있는 리드뮬러(ReedMuller) 부호, 리드솔로몬(Reed-Solomon) 부호, Golay 부호, 터보부호, LDPC 부호를 적용하여 양자오류를 보호하기 위한 시도들이 지속되었다[9].
이러한 부호들은 재귀적 부호화를 통해서, 오류 보정의 세기(Strength)를 높일 수 있기 때문에 연접(Concatenated) 부호라고 불린다. 최근 들어서는 상대적으로 높은 하드웨어 요구사항(낮은 오류 임계값)으로 인해서 주목도가 덜하지만, 효과적인 오류 복호화 등 결함허용 양자컴퓨팅 실현에 요구되는 장점을 갖추고 있는 부호이다.
Surface code[10,11], color code[12] 등으로 대표되는 위상학적 양자부호(Topological Code)는 높은 오류 임계값을 갖고 있어, 결함허용 양자컴퓨팅 실현 측면에서 주목받고 있다. 현재 보고되고 있는 양자컴퓨팅 하드웨어의 오류율이 위상학적 양자부호가 효과적으로 동작할 수 있는 하드웨어 안정성 기준에 도달하고 있기 때문에, 양자컴퓨팅 하드웨어 벤치마크 실험의 대상으로 해당 부호들이 활용되고 있다. 반면, 부호이론 자체가 하드웨어의 구조적 특성에 종속적이어서 해당 부호를 실현하기 위해 요구되는 양자컴퓨팅 하드웨어 구조(예: 2D 격자구조)가 정해져 있는데, 그러한 하드웨어를 개발하는 것이 쉬운 일은 아니다. 이외에도 높은 오류 복호화 복잡도 등 실시간 결함허용 양자컴퓨팅 실현을 위해 해결해야 할 점들이 아직은 많이 존재한다.
앞서, 결함허용 양자컴퓨팅은 하드웨어에 발생하는 양자오류를 소프트웨어 요소들로 극복해서 오류 효과가 컴퓨팅 결과에 제한적으로 영향을 미치는 기술이라 언급하였다. 그리고, 관련 소프트웨어 요소들에 대해서 간략하게 나열하였다. 하지만, 이러한 소프트웨어 요소들이 잘 갖춰져 있다고 해서 양자오류에 대한 억제가 무조건적으로 효과적인 것은 아니다. 소프트웨어에서 요구하는 내용들이 하드웨어적으로 잘 구현될 수 있어야 한다. 예를 들어, 양자오류보정의 회복(Recovery)연산은 오류신드롬 측정 결과에 따라 달라지고, 일부 결함허용 프로토콜은 비결정론적으로 구성되기도 한다. 즉, 소프트웨어적으로 결정되는 차기 양자연산이 하드웨어적으로 신속하게 실행될 수 있도록 큐비트 상태 조정(Feedback Control) 등이 고속으로 실행될 수 있어야 한다. 양자컴퓨팅에서의 데이터 처리 지연은 컴퓨팅 소요 시간이 오래 걸리는 것에 머무르지 않고, 컴퓨팅 결과의 오류를 의미한다.
Ⅲ. 논리적 큐비트 구현 동향
게이트 기반 양자컴퓨팅을 위해서는 각 큐비트의 양자 상태를 제어하고 읽어 낼 수 있어야 한다. 큐비트의 두 양자 상태 (|0>과 |1>)는 에너지 차이를 의미하고, 그 차이에 해당하는 에너지(포톤)를 큐비트에 인가함으로써 임의의 큐비트의 상태를 조절할 수 있게 된다. 따라서, 큐비트가 열적 잡음이 높은 환경에 놓여 있는 경우 양자 상태를 임의로 조절하거나 관측할 수 없기 때문에 작게는 수 켈빈에서 밀리켈빈에 이르는 온도환경에 큐비트를 설치하여 큐비트의 기저상태를 만들고 이와 더불어 각 큐비트 제어용 신호선(고주파 혹은 광 채널)을 상온에 설비된 고주파 전자기 장비와 연결해 큐비트 시스템을 운영하고 있다.
현재까지 핵자기공명(NMR: Nuclear Magnetic Resonance)[13,14], 포획이온(Trapped Ion)[15,16], 초전도 큐비트(Superconducting Qubit)[17-19], 그리고 반도체 양자점 기반 스핀 큐비트(Quantum Dot Spin Qubit)[20] 시스템들을 이용해 결함허용 양자컴퓨팅 기술 구현을 위한 기초 실험들과 그 가능성 증명에 대한 실험들이 진행되고 있다(그림 1)[21-23].
그림 1
주요 개발 큐비트 시스템: (a) Quantum dot spin qubit, (b) Superconducting qubit, (c) Trapped ion qubit
출처 (a) Reprinted with permission from [21], CC-BY 4.0. (b) Reprinted with permission from [22], CC-BY 4.0. (c) Reprinted with permission from [23], CC-BY 4.0.

포획이온 큐비트 시스템은 앞서 열거한 큐비트 시스템 중 가장 낮은 오류율을 선보였으며 큐비트 간 높은 연결성 등이 강점으로 제시되고 있다. 한편, 반도체 스핀 큐비트의 경우 현재까지 산업에서 개발되었던 공정을 사용할 수 있는 점과 높은 집적도를 구현할 가능성이 있으나, 현재까지 초전도 큐비트 시스템이 큐비트를 집적시키는 데 앞서 있다. 이어지는 절에서 각 큐비트 시스템에서 보고된 대표적인 QEC 구현사례와 개략적인 현황을 소개한다.
1. 초전도 큐비트 시스템
최근 Google은 자체 개발한 초전도 53-큐비트 양자칩 Sycamore 프로세서[24]를 이용하여 현재까지 보고된 최대 규모의 QEC 실험을 수행하였고, 결함 허용 양자컴퓨팅의 핵심이론인 Accuracy Threshold가 실제 상황에서도 성립할 수 있음을 일부 보여 주었다[19].
Accuracy Threshold는 앞서 살펴본 바와 같이 결함허용 양자컴퓨팅의 근간을 이루는 이론으로 일정 수준 이하의 오류가 발생하는 환경에서 논리 큐비트의 규모(물리 큐비트 개수)를 증가시킬수록 더욱 안정적인 논리 큐비트 연산이 가능함을 보여준다. 그동안 QEC의 효과에 관해서는 여러 실험 결과들이 보고된 적이 있지만, Accuracy Threshold를 입증할 수 있는 실험 결과는 보고된 적이 거의 없는데, 양자칩 규모가 그러한 실험을 지원할 수준이 되지 못한 점도 있지만, 주기적인 QEC 실험을 수행하는 과정에서 발생할 수 있는 leakage 오류 등을 온전히 제어하는 것이 어려웠기 때문이다.
Google은 앞서 발표한 leakage 오류 제어기술[25]을 적용해서, leakage 오류를 통제하는 가운데 반복 부호의 논리 큐비트 블록의 크기를 5에서 21로 점진적으로 증가하며, 논리 큐비트의 오류율 측정 실험을 수행하였다. 비록, Bit-Flip(또는 Phase-Flip) 오류만을 대상으로 하는 부분적인 양자오류보정 실험이지만, 데이터 블록의 크기가 증가하면, 논리 큐비트의 오류율이 지수적으로 감소함을 보였다(그림 2).
그림 2
Repetition code의 Data Block 길이 증가에 따른 Logical Error Rate 감소
출처 Reprinted with permission from [19], CC-BY 4.0.
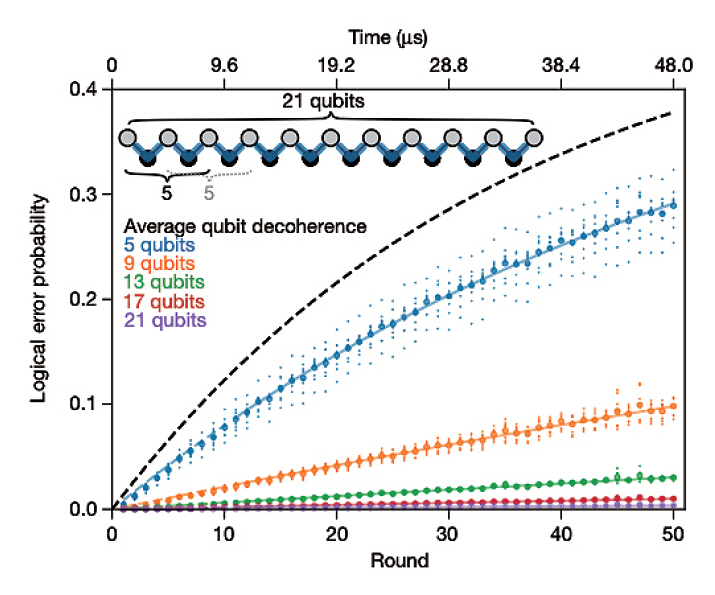
이러한 내용은 이론적으로는 당연하게 믿어지는 것이지만, 실험으로 보고된 것은 거의 첫 번째 사례이며, 논리 큐비트의 블록 크기가 증가함에 따라 논리 큐비트 오류율 감소 정도에 대한 수치도 제시하였다. 해당 수치는 Google 연구팀이 자체적으로 예측한 이론적 수치와 거의 유사하게 나타나 Accuracy Threshold가 실험적으로도 성립함을 보여 준 매우 중요한 사례라 할 수 있다.
2. 이온트랩 큐비트 시스템
Google 연구팀이 보여 준 Accuracy Threshold에 대한 실험적 입증 외에 중요한 결함허용 양자컴퓨팅 관련 실험적 milestone은 주기적으로 QEC를 수행하면서 양자 알고리즘의 논리적 게이트를 실행하는 것이다. 즉, 실시간 QEC가 실현 가능함을 보이는 것이 중요한 일인데, 그동안 주로 보고된 결과들은 QEC 또는 논리 게이트 각각에 대한 개별적 실험 결과들이 주를 이루었다.
2021년 Honeywell에서는 10큐비트 이온트랩 양자컴퓨터를 이용해서 ((7,1,3)) Steane code(그림 3 참조) 논리 큐비트 한 개를 대상으로 논리 큐비트 부호화, 논리 게이트와 QEC를 순차적으로 수행한 실험 결과를 보고하였다[26]. 특히, 논리 큐비트 부호화 및 QEC 수행과정에서 일부 과정의 생략 없이 표준적인 QEC 절차(반복적인 신드롬 측정, 실시간 복호화 및 Pauli 프레임 테이블 업데이트)를 모두 수행함으로써 실시간 QEC가 가능함을 보인 것이 매우 중요한 결과이다(그림 4).
그림 3
((7,1,3)) Steane code 구조 (순서가 매겨진 노드가 데이터 큐비트를 의미하고, 그렇지 않은 노드는 신드롬 큐비트를 의미함)
출처 Reprinted with permission from [26], CC-BY 4.0.
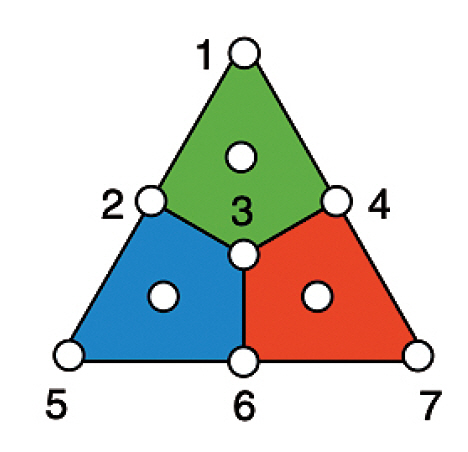
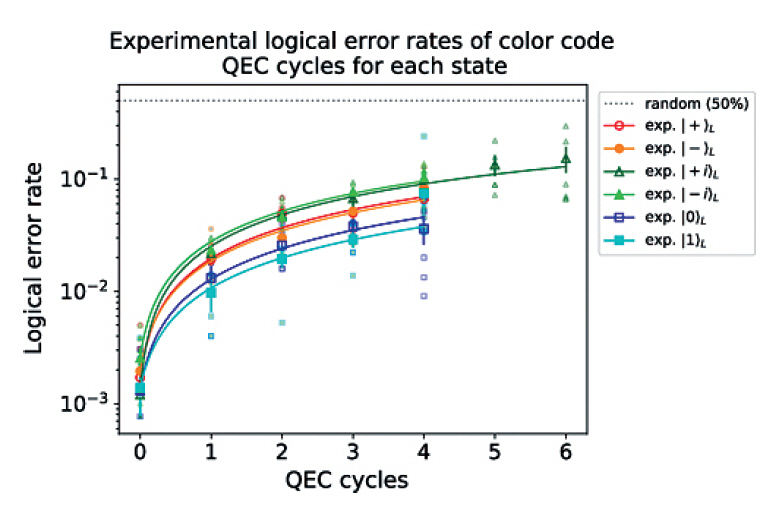
그림 4
QEC 사이클을 반복하여 측정한 logical state에 대한 오류율과 시뮬레이션 결과의 비교
출처 Reprinted with permission from [26], CC-BY 4.0.
3. 반도체 큐비트 시스템
반도체 양자점 큐비트 시스템 또한 다른 큐비트 시스템에 견줄만한 수준의 양자 게이트 신뢰도가 속속 보고되고 있다. 네덜란드 QuTech에서는 99.65%의 CZ 게이트를 구현하여 세계 최고의 양자점 큐비트의 게이트 신뢰도를 구현한 바 있으며[21], 호주 UNSW에서는 98.0%의 CZ 게이트를 구현하였으며[27], 일본 RIKEN에서는 2큐비트 얽힘 상태를 94.1%의 신뢰도로 구현하였다(표 1)[28].
한편, 오류 정정 회로 구현 상황으로는 최근 RIKEN에서 보고한 3-스핀 큐비트 위상 오류 정정 회로 구현의 예를 들 수 있다[20]. 논리 큐비트를 만드는 부호화 과정의 경우 CNOT 게이트가 두 개 사용되게 되는데, RIKEN은 CZ/2 게이트를 네 개 사용하여 논리 큐비트의 초기화 과정을 구현하였다. 복호화가 완료된 초기화 상태를 양자상태 토모그래피를 이용하여 분석한 결과 86.6%의 인코딩 신뢰도로 75%의 기준 구분점을 넘어섰다.
양자오류 발생 시 오류를 정정하는 게이트는 3- 큐비트 iToffoli 게이트를 사용하였다. 보고된 논문에서는 iToffoli 게이트를 사용하여 기존 Toffoli 게이트와 동등한 연산 결과를 갖는 회로를 적용할 수 있었고. 양자상태 토모그래피 방법을 이용하여 게이트 신뢰도가 96%에 해당함을 보고하였다.
논리적 큐비트를 형성한 뒤 신뢰도를 두 가지 방법으로 평가하였다. 첫 번째로, 그림 5의 결풀림(Dephasing) 과정에서 양자 오류를 발생시켜 양자오류보정 회로의 정확성을 평가하였다. 결풀림 과정에서는 반도체 큐빗비트 시스템에서 자연적으로 발생하는 오류에 대응하여 양자 상태를 얼마나 잘 보존할 수 있는지를 평가하는 과정이다. 논리적 큐비트로 부호화한 후에, 연산을 수행하지 않는다면 자연 발생 오류가 인가되고, 그 후에 복호화하여 발생한 오류를 정정한다. 최근 보고된 결과[25]에서는, 양자점 큐비트로 구성된 논리적 큐비트가 물리적 큐비트에 비교하여 우수한 구간은 없었다.
그림 5
양자 오류 정정 회로 순서. 부호화-결풀림-복호화-회복(오류 정정)-상태 측정 과정을 거침
출처 Reprinted with permission from [29], CC-BY 3.0

본 평가 방법은 물리적 큐비트에 비하여 논리적 큐비트의 신뢰도가 높은 구간이 없어서 일견 효용성이 없다고 판단할 수 있다. 그러나 본 평가 방법은 다음과 같은 중요한 의의를 갖는다. 첫 번째로, 이 평가 방식의 경우, 임의의 오류를 발생시킨 것이 아니므로 양자컴퓨팅을 구동하는 경우와 더 유사한 상황이라고 할 수 있다. 그 결과, 양자회로의 구성 및 최소 게이트 구동 신뢰도 요구조건 등에 따라 실제적 양자컴퓨팅의 구동 성능을 얼마나 향상해야 하는지 판단 지표로 사용할 수 있다. 두 번째, 자연 발생 오류 정도를 판단할 수 있다. 논리적 큐비트를 형성하는 것은 어떠한 구간에서라도 효과를 입증할 수 있는 것은 아니다. 앞서 임의의 오류를 인가하여 평가한 경우에서처럼, 오류 정도가 크지 않은 경우에는 논리적 큐비트를 구성하더라도 신뢰도 측면에서 손실을 입을 수 있다. 이에 따라, 본 평가 결과 자연 발생 오류가 충분히 적다는 점을 확인할 수 있었다.
두 번째 논리적 큐비트 신뢰도 평가방법은 각 큐비트에 위상 오류 한 개를 임의 발생시켜 오류보정 신뢰도를 확인하는 방법이다. 그림 5의 결풀림 과정을 양자 위상 오류를 인위적으로 발생하는 과정으로 변경하였다. 그 결과[25], 위상 오류가 매우 작은 경우에는, 물리적 큐비트가 논리적 큐비트보다 우수한 성능을 보였다. 위와 같은 인위적 오류를 삽입하여, 양자점 큐비트[25]와 초전도 큐비트[17] 모두 3-큐빗 양자 오류 정정 코드를 적용하였을 때 위상 오류의 크기에 따라 유사한 결과를 보였다.
오류의 크기가 매우 작을 때에 논리적 큐비트는 부호화, 복호화, 오류 보정 과정을 거치기 때문에, 부정확한 게이트 구동에 따라 오류가 누적될 수 있지만, 물리적 큐비트는 연산 자체의 오류만 반영된다. 이에 물리적 큐비트가 논리적 큐비트의 신뢰도에 비하여 더 높은 신뢰도를 보일 수 있다.
Ⅲ. 결론 및 제언
본고에서 결함허용 양자컴퓨팅 연구개발의 소개와 전반적인 연구개발 동향과 현황들에 대해 살펴보았다. 현재까지 개발된 QEC 프로토콜은 실질적인 결함허용 양자컴퓨터 구현을 위한 기준을 제시하고 있으며, 최근 초전도, 이온트랩 그리고 반도체 양자점 큐비트 등 다양한 양자컴퓨팅 플랫폼에 대하여 QEC 프로토콜을 적용하려는 결함허용 양자컴퓨팅의 실험적 노력이 지속적으로 이어지고 있다. 초전도 큐비트의 경우 Google에서 큐비트 증가당 논리적 오류율 감소율을 실험적으로 구현하고 이론적 예상치로 검증하여 결함허용 이론이 실제 물리적 실험을 통해서도 실현 가능함을 보고하고 있다. 또한 허니웰의 이온트랩 양자컴퓨터에서 주기적으로 QEC를 수행하면서 양자 알고리즘의 논리적 게이트를 실행함으로써 실시간 QEC가 실현 가능함을 보여 주는 결과를 보고하였다. 그리고, 반도체 양자점 큐비트에서는 3-큐비트 양자오류보정 회로를 구성하여 그 기본적인 특성을 시연하여 한 걸음 더 나아가고 있다. 이렇듯 전 세계적으로 활발히 연구가 진행 중에도 불구하고 상용화 단계로 가기 위해서는 현재의 기술 수준의 기술 성숙이 더욱 요구되고 있다.
결함허용 양자컴퓨팅은 기본적으로 논리적 큐비트를 만들 수 있을 만큼 물리적 큐비트의 오류율이 충분히 낮아야 한다. 또한 많은 수의 물리적 큐비트 수를 요구하고, 이에 동반하여 큐비트 제어 자원도 증가하여 이를 간단하고 신속하게 제어할 수도 있어야 한다. 그리고 시스템 전반에 걸쳐 오류가 있더라도 원하는 오류 보정이 가능한 결함허용적 설계에 따라 최적화되어 구현되어야 하기 때문에 결함 허용 컴퓨팅은 높은 기술 수준을 요구하고 있다. 그럼에도 불구하고 결함허용 양자컴퓨팅은 궁극적인 양자컴퓨팅 기술로 모든 알고리즘에 활용할 수 있고 사회 전반에 걸쳐 혁신적인 변화를 가져올 수 있기 때문에 그 파급효과가 크다. 결과적으로 미래의 양자컴퓨팅 기술은 현재의 NISQ 시대의 한계를 뛰어넘어 궁극적으로 결함허용 양자컴퓨팅 기술의 시대로 도약할 것으로 보인다. 따라서 이에 대비하여 결함허용 양자컴퓨팅 전반에 걸친 기초 및 원천 기술 연구개발이 이루어져야 하며, 미래 우리나라 양자컴퓨팅 연구개발에 있어 그 필요성과 중요성은 날로 커지고 있다.
용어해설
큐비트(Qubit) 0과 1의 양자 상태를 중첩과 얽힘 현상을 이용하여 표현하는 양자컴퓨팅 연산의 기본 단위로 Quantum bit의 줄임 표현
물리적 큐비트(Physical Qubit) 물리적으로 구현된 개별적 큐비트
논리적 큐비트(Logical Qubit) 다수의 물리적 큐비트로 구성된 한 개의 오류가 보정된 큐비트 그룹으로 시간에 따라 양자 상태를 안정적으로 보존하며 연산 진행 가능. 데이터를 인코딩한 큐비트 부근에 보조 큐비트를 배치하여, 데이터 큐비트를 직접 측정하지 않고 보조 큐비트로만 측정하여 오류를 찾아내고 보정하게 구성됨
양자오류정정(QEC) 양자 정보 처리용 큐비트에 발생한 양자 오류를 정정하는 기술
얽힘 게이트(Entangled Gate) 2개 이상의 큐비트의 상태가 서로 의존적인 (얽힌) 상태로 만드는 양자 게이트
GHZ 상태 3큐비트에 대한 특정 유형의 얽힌 양자 상태
Toffoli 게이트 Controlled-Controlled-Not(CCNOT) 게이트로 범용 가역 논리 게이트라 부르며 처음 두 비트가 모두 1로 설정되면 세 번째 비트가 반전되고, 그렇지 않으면 모든 비트가 동일하게 유지됨
약어 정리
A. Steane, "Introduction to quantum error correction," Phil. Trans. R. Soc. A., vol. 356, 1998, pp. 1739-1758.
J. Preskill, "Fault-tolerant quantum computation," in Introduction to Quantum Computation and Information, World Scientific Publishing, Singapore, Singapore, 1998, pp. 213-269.
N.J. Ross and P. Selinger, "Optimal ancilla-free Clifford+T approximation of z-rotation," Quantum Inform. Comput., vol. 16, no. 11-12, 2016, pp. 901-953.
V. Kliuchnikov et al., "Fast and efficient exact synthesis of single qubit unitaries generated by Clifford and T gates," Quantum Inform. Comput., vol. 13, no. 7-8, 2013, pp. 607-630.
T. Jochym-O’Connor et al., "Disjointness of stabilizer codes and limitations on fault-tolerant logical gates," Phys. Rev. X, vol. 8, no. 2, 2018, article no. 21047.
P. Aliferis et al., "Quantum accuracy threshold for concatenated distance-3 codes," Quantum Inform. Comput., vol. 6, no. 2, 2006, pp. 97-165.
P.W. Shor, "Scheme for reducing decoherence in quantum computer memory," Phys. Rev. A, vol. 52, no. 4, 1995, article no. R2493.
A. Steane, "Multiple-particle inteference and quantum error correction," Proc. R. Soc. Lond. A, vol. 452, no. 1954, 1996, pp. 2551-2577.
D.A. Lidar and T.A. Brun, Quantum Error Correction, Cambridge University Press, Cambridge, England, 2013.
A.Y. Kitaev, "Fault-tolerant quantum computation by anyons," Ann. Phys., vol. 303, no. 1, 2003, pp. 2-30.
R. Raussendorf and J. Harrington, "Fault-tolerant quantum computation with high threshold in two dimensions," Phys. Rev. Lett., vol. 98, no. 9, 2007, article no. 190504.
H. Bombin and M.A. Martin-Delgado, "Topological quantum distillation," Phys. Rev. Lett., vol. 97, no. 18, 2006, article no. 180501.
D.G. Cory et al., "Experimental quantum error correction," Phys. Rev. Lett., vol. 81, no. 10, 1998, pp. 2152-2155.
E. Knill et al., "Benchmarking quantum computers: The five-qubit error correcting code," Phys. Rev. Lett., vol. 86, no. 25, 2001, pp. 5811-5814.
P. Schindler et al., "Experimental repetitive quantum error correction," Science, vol. 332, no. 6033, 2011, pp. 1059-1061.
L. Egan et al., "Fault-tolerant control of an error-corrected qubit," Nature, vol. 598, 2021, pp. 281-286.
M.D. Reed et al., "Realization of three-qubit quantum error correction with superconducting circuits," Nature, vol. 482, 2021, pp. 382-385.
J. Kelly et al., "State preservation by repetitive error detection in a superconducting quantum circuit," Nature, vol. 519, 2015, pp. 66-69.
G.Q. AI, "Exponential suppression of bit or phase errors with cyclic error correction," Nature, vol. 595, 2021, pp. 383-387.
K. Takeda et al., "Quantum error correction with silicon spin qubits," arXiv preprint, CoRR, 2022, arXiv: 2201.08581.
X. Xue et al., "Quantum logic with spin qubits crossing the surface code threshold," Nature, vol. 601, 2022, pp. 343-347.
A.D. Corcoles et al., "Demonstration of a quantum error detection code using a square lattice of four superconducting qubits," Nat. Commun., vol. 6, 2015, article no. 6979.
K. Brown, J. Kim, and C. Monroe, "Co-designing a scalable quantum computer with trapped atomic ions," NPJ Quantum Inf., vol. 2, 2016, article no. 16034.
F. Arute et al., "Quantum supremacy using a programmable superconducting processor," Nature, vol. 574, 2019, pp. 505-510.
M. McEwen et al., "Removing leakage-induced correlated errors in superconducting quantum error correction," Nat. Commun., vol. 12, 2021, article no. 1761.
C. Ryan-Anderson et al., "Realization of real-time fault-tolerant quantum error correction," Phys. Rev. X, vol. 11, 2021, article no. 041058.
W. Huang et al., "Fidelity benchmarks for two-qubit gates in silicon," Nature, vol. 569, 2019, pp. 532-536.
A. Noiri et al., "A shuttling-based two-qubit logic gate for linking distant silicon quantum processors," arXiv preprint, CoRR, 2022, arXiv: 202.01357 [quant-ph].
그림 1
주요 개발 큐비트 시스템: (a) Quantum dot spin qubit, (b) Superconducting qubit, (c) Trapped ion qubit
출처 (a) Reprinted with permission from [21], CC-BY 4.0. (b) Reprinted with permission from [22], CC-BY 4.0. (c) Reprinted with permission from [23], CC-BY 4.0.

그림 2
Repetition code의 Data Block 길이 증가에 따른 Logical Error Rate 감소
출처 Reprinted with permission from [19], CC-BY 4.0.
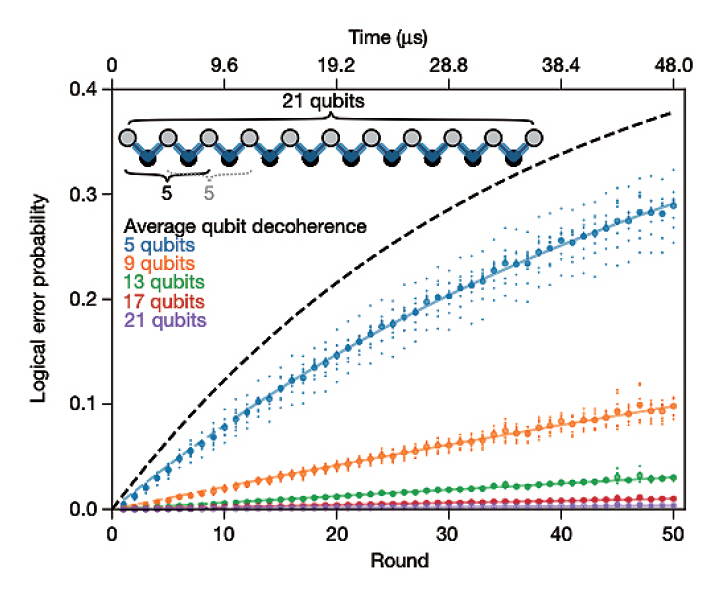
그림 3
((7,1,3)) Steane code 구조 (순서가 매겨진 노드가 데이터 큐비트를 의미하고, 그렇지 않은 노드는 신드롬 큐비트를 의미함)
출처 Reprinted with permission from [26], CC-BY 4.0.
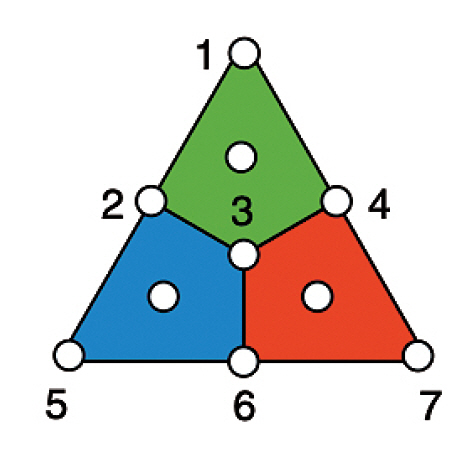
그림 4
QEC 사이클을 반복하여 측정한 logical state에 대한 오류율과 시뮬레이션 결과의 비교
출처 Reprinted with permission from [26], CC-BY 4.0.
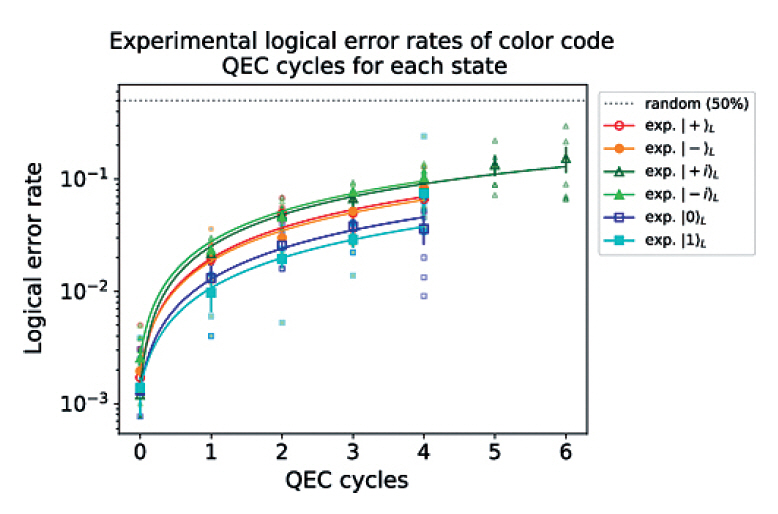
그림 5
양자 오류 정정 회로 순서. 부호화-결풀림-복호화-회복(오류 정정)-상태 측정 과정을 거침
출처 Reprinted with permission from [29], CC-BY 3.0

- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.