결함허용 양자 컴퓨팅을 위한 양자 오류 복호기 연구 동향
Research Trends in Quantum Error Decoders for Fault-Tolerant Quantum Computing
- 저자
-
조은영클라우드기반SW연구실 eycho@etri.re.kr 온진호클라우드기반SW연구실 onjinho@etri.re.kr 김재열클라우드기반SW연구실 gauri@etri.re.kr 차규일클라우드기반SW연구실 gicha@etri.re.kr
- 권호
- 38권 5호 (통권 204)
- 논문구분
- 인공지능컴퓨팅 기술 동향
- 페이지
- 34-50
- 발행일자
- 2023.10.01
- DOI
- 10.22648/ETRI.2023.J.380504
 본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.
본 저작물은 공공누리 제4유형: 출처표시 + 상업적이용금지 + 변경금지 조건에 따라 이용할 수 있습니다.- 초록
- Quantum error correction is a key technology for achieving fault-tolerant quantum computation. Finding the best decoding solution to a single error syndrome pattern counteracting multiple errors is an NP-hard problem. Consequently, error decoding is one of the most expensive processes to protect the information in a logical qubit. Recent research on quantum error decoding has been focused on developing conventional and neural-network-based decoding algorithms to satisfy accuracy, speed, and scalability requirements. Although conventional decoding methods have notably improved accuracy in short codes, they face many challenges regarding speed and scalability in long codes. To overcome such problems, machine learning has been extensively applied to neural-network-based error decoding with meaningful results. Nevertheless, when using neural-network-based decoders alone, the learning cost grows exponentially with the code size. To prevent this problem, hierarchical error decoding has been devised by combining conventional and neural-network-based decoders. In addition, research on quantum error decoding is aimed at reducing the spacetime decoding cost and solving the backlog problem caused by decoding delays when using hardware-implemented decoders in cryogenic environments. We review the latest research trends in decoders for quantum error correction with high accuracy, neural-network-based quantum error decoders with high speed and scalability, and hardware-based quantum error decoders implemented in real qubit operating environments.
Share
Ⅰ. 서론
상용 양자 컴퓨터 구축의 가장 큰 장벽은 결어긋남(Decoherence)과 외부 환경적 요인에 의해 발생하는 큐비트 오류이다. 양자 오류정정(QEC: Quantum Error Correction) 기술은 이 문제를 극복하고 신뢰성 있는 양자 컴퓨터를 구축하기 위한 선결 과제다. 현재까지는 고전적인 오류정정 개념을 차용하여 다양한 방식의 양자 오류정정부호가 제안[1,2]되어 왔다.
일반적으로 양자 오류정정부호에서 양자 오류 복호화(QED: Quantum Error Decoding) 시스템이 고려해야 할 몇 가지 요소가 있다. 첫째, 양자 컴퓨팅 기술은 큐비트 측정에 따른 상태 붕괴 특성으로 계산 과정에서 데이터 큐비트를 직접 접근하는 대신 얽힘 관계의 보조 큐비트(AQ: Auxiliary Qubit)를 사용하여 연산을 처리한다. 이런 이유로 양자 오류정정 주기에서 양자 오류 복호화에 요구되는 시공간 비용은 상당히 고가이다. 둘째, 양자 컴퓨터의 코드 규모가 증가함에 따라 신드롬(Syndrome) 측정 주기 내 오류 복호화 처리가 완료되지 못해서 신드롬이 누적되는 백로그 문제도 고려해야 한다. 마지막으로, 양자 오류 복호화는 하나의 신드롬 패턴이 다양한 오류 조합 상태로 해석될 수 있는 일대다 대응관계를 갖고 있어서 논리 큐비트 규모(즉, 코드 크기)가 증가하는 경우 오류 복호화 계산 복잡도가 기하급수적으로 증가하는 NP-hard 문제에 해당한다. 따라서 양자 오류 복호화 시스템에서 코드 규모 증가에 따른 확장성도 중요한 고려 요소가 된다.
최근 양자 오류정정부호 중 가장 인지도가 높은 기술은 표면코드(SC: Surface Code)다. 이 코드는 초전도체 양자 컴퓨터의 큐비트 연결성 제약을 효과적으로 극복하고 높은 오류 임계값 특성을 갖는다. 본고에서는 이 표면코드를 중심으로 양자 오류 복호화 요구사항을 간단히 살펴보고 구현 방식에 따라 주요 연구 사례를 분류한 최신 오류 복호기 기술 동향을 소개하고자 한다. 이를 위해, 먼저 Ⅱ장에서는 오류 복호기를 이해하기 위한 용어, 기술 개념 등 오류 복호기의 개요를 간략히 정리하여 주요 연구 사례에서 해결하고자 하는 문제를 파악하고자 한다. Ⅲ장에서는 물리 큐비트 또는 논리 큐비트 수준에서 오류를 식별하는 고전 알고리즘 방식의 오류 복호기를 소개한다. Ⅳ장에서는 2017년 이래 연구가 활발히 진행되고 있는 신경망 알고리즘 기반의 오류 복호기에 대한 최신 연구 동향을 살펴본다. Ⅴ장에서는 오류 복호화 처리 성능 향상과 극저온 환경에서 복호기의 저전력 성능 달성을 목표로 연구가 진행되고 있는 하드웨어 방식 오류 복호기의 최신 연구 사례를 정리하였다. 마지막으로 Ⅵ장은 오류 복호기의 연구 동향을 최종적으로 요약한다.
Ⅱ. 양자 오류 복호기의 개요
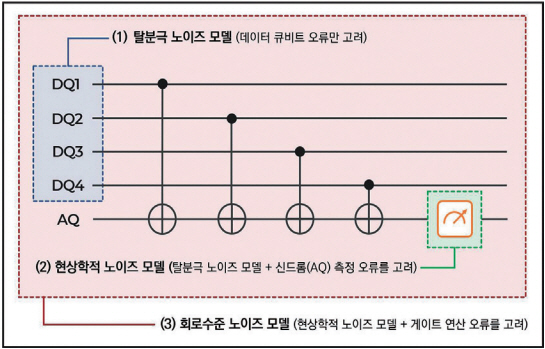
양자 컴퓨터는 큐비트 상태에 노이즈를 유발하는 다양한 요소가 존재한다. 양자 오류정정 분야의 다양한 문헌에서 사용되는 오류(Error)는 컴퓨팅 관점에서 계산 결과에 미치는 영향을 중심으로 규정한 용어인 반면, 노이즈(Noise)는 큐비트 상태 관점에서 의도치 않은 상태 변화를 규정하는 용어다. 그림 1은 표면코드상에서 Z 안정기(Stabilizer) 신드롬 측정에 사용되는 양자 회로를 중심으로 세 가지 유형의 노이즈 모델에 대해 설명한다.
(1) 탈분극 노이즈 모델(Depolarization Noise Model)은 데이터 큐비트(DQ: Data Qubit) 자체에 Pauli X, Y, Z 연산의 상태 변화가 동일 확률로 발생하는 모델이다. (2) 현상학적 노이즈 모델(Phenomenological Noise Model)은 탈분극 노이즈 모델에 더하여 보조 큐비트(AQ)상의 오류 신드롬 측정 오류가 추가된 모델이다. 마지막으로 (3) 회로수준 노이즈 모델(Circuit-level Noise Model)은 DQ와 AQ 등의 모든 큐비트에 대해 연산을 수행할 때 발생할 수 있는 게이트 연산 오류를 포함하는 모델이다. 일반적으로 이 모델이 실제 양자 컴퓨팅에서 노이즈를 설명할 때 사용할 수 있는 가장 현실에 근접한 모델이다.
양자 오류정정부호의 성능을 나타내는 두 가지 척도가 있다. 첫 번째는 양자 오류정정부호가 특정 물리 큐비트 오류율 한계 내에서 코드거리(d: Distance)가 길수록 논리 큐비트의 오류율이 낮아진다는 특징과 관련된다. 오류정정부호에서 이 특정 한계 물리 오류율을 오류 임계값(Error Threshold)이라 한다. 두 번째 척도는 오류정정을 통해 논리 큐비트 오류율이 물리 큐비트 오류율보다 낮아지는 지점의 물리 오류율로 의사 임계값(Pth: Pseudo threshold)이라 정의한다. 결함허용 양자 컴퓨팅(FTQC: Fault-Tolerant Quantum Computing) 환경에서 오류정정부호의 성능은 양자 오류 복호기의 성능과 직결된다. 이런 이유로 양자 오류 복호기의 성능은 이 두 가지 척도로 언급되는데, 문헌에서는 오류 임계값과 의사 임계값에 대한 구체적인 구분 없이 사용하는 경우가 있으므로 오류율 수치를 확인하는 경우 문맥에 따라 구별하여 참고하는 것이 필요하다.
양자 오류 복호기 연구 분야에서 고려해야 하는 핵심 성능 지표 요소는 정확성(Accuracy), 저지연성(Speed), 확장성(Scalability)이다. 최근에는 여기에 더하여 양자 하드웨어, 오류정정코드, 노이즈 모델 등의 다양한 시스템적 요인에 효과적으로 대응할 수 있는 오류 복호화 알고리즘의 유연성(Flexibility)도 오류 복호기 성능 평가 시 고려되고 있다. 이 성능 지표의 정의를 요약하면 표 1과 같다.
표 1 오류 복호기의 주요 성능 지표
본고에서는 오류 복호기의 최신 연구 사례를 해당 성능 지표를 중심으로 살펴볼 예정이다. 다만, 오류 복호기의 구체적인 연구 사례를 설명하기에 앞서 주요 오류 복호화 알고리즘을 세 가지 성능 지표를 기준으로 간략히 분류해 보면 표 2와 같다.
표 2 주요 복호화 알고리즘의 성능 지표 비교
| 알고리즘 | 정확성 | 저지연성 | 확장성 |
|---|---|---|---|
| LUT | 매우 높음 | 낮음 | 매우 낮음 |
| TN | 매우 높음 | 보통 | 보통 |
| MWPM | 높음~매우 높음 | 보통 | 보통 |
| UF | 높음 | 낮음 | 높음 |
| ML | 높음 | 낮음 | 보통 |
2006년 Caltech의 Poulin[4]은 양자 오류 복호화 문제를 다루기 위해 오류 E를 S(Stabilizer Product), P(Pure Error), L(Logical Error)의 곱관계, 즉 E=S·P·L로 분해할 수 있음을 보여 주었다. 여기서 S 요소는 물리 양자 상태의 위상과 불변성 표현에 사용하는 게이지 연산자(Gauge Operator)와 안정기의 곱, P 요소는 순수 오류(Pure Error), 마지막으로 L 요소는 논리 Pauli 연산자이다. 오류 E는 물리 큐비트에 대해 직접 저수준 복호화 방식으로 오류를 예측한다. 반면, 상기 분해법으로 오류 복호화 문제를 고려하면 논리 큐비트 대상의 고수준 복호화 방식으로 오류 예측을 가능하게 한다. 일반적으로 순수 오류 P는 신속한 결정이 가능하므로 논리 오류 L의 논리적 오류 식별에 효과적인 복호화 기법을 적용함으로써 오류 복호화의 효율성을 높일 수 있다. 이에 대한 사례는 Ⅳ장의 신경망 오류 복호화 동향에서 더 자세히 살펴본다.
Ⅲ. 고전 알고리즘 방식 양자 오류 복호기
가장 대표적인 고전 알고리즘 방식의 양자 오류 복호기는 오류 큐비트의 위치를 효과적으로 추론하기 위해 그래프 알고리즘을 기반으로 한다. 표면코드에 대해 사용할 수 있는 대표적 고전 방식 오류 복호화 알고리즘의 특성은 표 3과 같다.
표 3 주요 고전 방식 오류 복호화 알고리즘의 특징
| 사례 | 알고리즘 | 오류 임계값 | dmax | 계산 복잡도 |
|---|---|---|---|---|
| Caltech (2004) [6] | MWPM | 0.154 | 63 | O(n3)~O(d2.11) |
| Caltech/MS/ICL (2021) [7] | UF | 0.146 | 127 | O(n·α(n)), α(n)≤3 |
| UdeS (2010) [8] | RG | 0.164 | 128 | O(d2logd)~O(logd) |
| UdeS/ETHZ (2021) [9] | TN | 0.188 | 64 | O(nlogn + nχ3) |
일반적으로 고전 알고리즘 방식의 오류 복호기는 다항 시간(Polynomial Time) 내에 오류 예측을 보장하고 다양한 노이즈 모델에 대해 한계 임계값에 근접하는 것으로 알려져 있다. 그러나 많은 계산량을 동반하고 있어 시스템 확장성이 낮다.
고전 알고리즘 방식 오류 복호기를 하드웨어로 구현하는 경우에도 처리 속도 및 저전력에 대한 요구사항을 충족시키기 어렵다. 이론적으로 정확성 측면에서 최고 성능을 보이는 복호화 알고리즘으로 최대 가능성 복호화(MLD: Maximum Likelihood Decoding) 기법이 있지만, 이 기법은 계산 복잡도가 상당히 높아 실제 환경에 직접적으로 적용할 수 없는 단점을 가진다.
다음은 대표적인 고전 알고리즘 방식을 중심으로 양자 오류 복호기의 연구 동향을 살펴본다.
1. MWPM
MWPM(Minimum Weight Perfect Matching) 복호기는 오류 신드롬과 일치하는 최소 가중치 오류 집합을 검출하는 기법이다. 2004년 Caltech의 Harrington[7]은 Toric Code에 최초로 MWPM 복호기를 적용하였다. 2014년 캘리포니아대학의 Fowler[10]는 메모리에 모든 오류 조합을 로드하고 선택하는 방식으로 계산 복잡도가 O(1)을 보이는 복호화 기법을 발표하였지만, 실제 구현 사례는 없는 것으로 알려져 있다.
2021년 UCL에서 공개한 PyMatching[11]은 표준 MWPM 복호화 알고리즘과 개선된 국소사상(Local Matching) 복호화 알고리즘을 동시에 포함한 대표적인 MWPM 오류 복호기다. 개선된 국소사상 복호화 알고리즘은 표준 MWPM 복호화 알고리즘과 오류 임계치는 거의 동일하지만 계산 복잡도는 2차 다항함수로 감소한다. 또한, 단순 격자에 대해 Dijkstra 알고리즘 대신 Manhattan 거리 또는 변환 대칭(Translational Symmetry) 알고리즘을 사용하는 등 추가 최적화 기법을 제공하고 있다. 2023년 공개된 PyMatching v2[12]에서는 새로운 트리로 시공간에 대한 병렬화를 허용하여 부가적인 속도 향상을 달성하였다. 같은 시기에 대만국립칭화대학의 Yuan[13]은 X 오류(비트반전)와 Z 오류(위상반전)의 상관관계를 통해 탈분극 채널의 Y 오류를 효과적으로 처리하는 IRMWPM(Iteratively Reweighted MWPM)을 제안하였다.
2. UF
대규모 양자 컴퓨터를 구축하려면 큐비트 오류를 고속으로 수정할 수 있어야 한다. UF(Union-Find) 복호기는 정확성 측면에서 MWPM과 유사한 성능을 나타내면서도 저지연성 측면에서 O(n) ~ O(3n)의 선형적인 계산 복잡도를 갖는 실행 시간을 보인다. 오류 복호기의 핵심 기능은 데이터 큐비트와 X, Z 오류 확인용 보조 큐비트로 구성된 클러스터를 성장시키면서 서로 만날 때 합치는 방식이다. 모든 오류 위치는 개별 오류 복구 후보로 초기화되고 각 오류 위치는 고유한 집합으로 처리된다. 그러고 나서 Union-Find 데이터 구조를 사용하여 오류 위치를 그룹화하고 연결한다. 여기서 오류 위치가 동일한 그룹은 동일한 오류 이벤트를 의미한다. 그룹화 프로세스에서는 오류 위치 간의 Union 및 Find 함수를 사용한다. 그룹화 완료 후 각 그룹에서 가장 확률이 높은 오류 복구 후보를 선택하고 그룹의 모든 오류 위치에 동시에 적용한다. 이러한 2단계 UF 복호기의 장점은 저지연성과 유연성으로 다른 기하 및 차원에서도 즉각적인 적용이 가능하다는 것이다.
2020년 Microsoft의 Delfosse[14]는 표면코드에 대해 lazy UF 복호기를 제안하였는데 저지연성 측면에서 기존 UF에 비해 10배, MWPM에 비해 50배 성능 향상을 달성하였다. 또한, 마이크로 구조의 효과적인 설계로 사용되는 하드웨어가 1,500배 감소하는 성과를 보였다는 점도 주목할 필요가 있다. 그러나 지금까지 살펴본 UF 복호기는 일부 양자 코드에 대해서는 최적성이 보장되지 않을 수 있으며, 복잡한 오류 패턴에 대한 복구 성능이 제한될 수 있는 문제를 여전히 갖는다.
3. RG
RG(Renormalization Group) 복호기는 통계 물리학의 재정규화 그룹 개념을 차용해서 개발되었다. 복호화 알고리즘은 양자 큐비트 구조를 특정 형태의 계층 셀로 나눈 후, 하부 셀 정보를 통합해서 상위 셀을 형성하는 과정을 최종 셀 통합 시까지 반복하는 방식으로 논리 큐비트의 오류를 탐지 및 수정한다. RG 복호화 알고리즘은 셀 정보 통합 방식에 따라 일반적으로 Hard-Decision RG(HDRG)와 Soft-Decision RG(SDRG)로 구분[15]된다.
IBM의 Bravyi와 Caltech의 Haah[16]이 제안한 HDRG 복호기는 하부 계층에서 각 셀의 상태를 결정하여 상위 계층으로 전파한다. 이런 특징으로 복호기 구현이 간단하고 전체 과정을 수학적으로 분석할 수 있어 실행에 대한 정밀한 분석이 가능하다. UdeS의 Duclos-Cianci, Poulin[17]이 제안한 SDRG 복호기는 계층의 셀 통합 반복 과정에서 각 셀에 추정된 확률값을 할당하고 최종 단계에서 통합 확률을 기반으로 논리 큐비트의 최종 상태를 추정하는 방식을 사용한다. 이 방식은 HDRG 복호기에 비해 계산 복잡도가 높고 최종 상태 결과에 대해 정밀한 분석이 불가능해 임계값을 통한 수치적인 성능 증거만을 제공하는 제약이 있다. 그럼에도 불구하고 SDRG 복호기는 HDRG 복호기에 비해 더 좋은 오류 임계값과 오류억제가 가능하다.
RG 복호기는 계층의 각 셀에 대해 독립 연산이 수행되므로 복호화 병렬 처리가 가능해 O(d2logd ~ logd)의 계산 복잡도를 갖는다. 다수 오류가 발생하는 대규모 양자 시스템에서 이런 수준의 계산 복잡도는 빠른 복호화 실행 수준으로 다른 복호화 알고리즘에 비해 성능이 우수하다. 이런 이유로 RG 복호기는 다양한 다계층, 다단계 복호기 연구에서 전처리 또는 후처리 복호기로 광범위하게 활용[18]되고 있다.
4. TN
2014년 UdeS의 Ferris, Poulin[19,20]은 양자 오류정정과 Tensor Network 연산의 유사점을 파악하고, Tensor Network 연산 기법을 다양한 오류정정부호에 적용하였다. 이 과정에서 분할 방식 branching MERA(Multi-scale Entanglement Renormalization Ansatz)의 가능성을 확인하였고 이를 일반화하여 TN(Tensor Network) 복호기를 제안하였다.
2021년 ETH Zurich와 UdeS 연구진[21]은 TN 복호기를 물리 큐비트 오류 판단에 적용하였다. TN 복호기는 오류 복호화 최적화 문제를 TN 수축(Contraction) 문제로 변환 처리하는 기법을 사용하고 있으며, 한계 오류 임계값에 근접하는 높은 성능을 보이고 있다. 비트반전, 위상반전 오류를 갖는 탈분극 노이즈 모델을 대상으로 규칙 또는 불규칙 표면코드 및 색상 코드 등에서 성능을 확인하였다. 이 방식은 2D Pauli 코드에 대한 범용 복호기로서 작동할 수 있음이 입증되었으며 X/Z/Y 오류나 측정 오류, 고차원 LDPC(Low-Density Parity-Check) 코드 등으로의 확장이 가능하여 FTQC 환경에서 특히 정확성과 유연성 요소의 장점을 갖는다. 이 TN 복호기는 Toric Code에서 d=64까지 실험적으로 적용한 사례다.
Ⅳ. 신경망 알고리즘 기반 양자 오류 복호기
고전 복호화 알고리즘은 큐비트 오류 상황에 따라 복호화 계산 비용이 가변적으로 결정되므로 제한된 시간 내 복호화 처리가 완료되어야 하는 양자 컴퓨팅 특성상 확장성 측면에서 근본적 한계를 노출한다. 이런 상황에서 2017년부터 신경망(NN: Neural Network) 알고리즘 기술을 양자 오류 복호기에 적용한 연구 사례가 다수 등장하였다. 표 4에서는 순방향신경망(FFNN: Feed-Forward NN), 합성곱 신경망(CNN: Convolutional NN), 순환신경망(RNN: Recurrent NN) 등 다양한 신경망 알고리즘 기법을 적용한 신경망 기반 오류 복호기 연구 사례 현황을 간략히 정리하였다.
표 4 신경망 기반 오류 복호기 연구 사례
| 사례 | 알고리즘 | 오류정정부호 | 노이즈 모델 | 오류 임계값 | dmax | 계산 복잡도 |
|---|---|---|---|---|---|---|
| TU Delft(2017) [22] | FFNN | Surface Code | 탈분극 | ~0.15 | 7 | O(MWPM) |
| Waterloo Univ.(2017) [23] | Restricted BM | Toric Code | i.i.d. 비트반전 | ~0.110 | 6 | > O(MWPM) |
| Yale Univ.(2017) [24] | FFNN | Toric Code | 탈분극 | 0.164 | 11 | >> O(MWPM) |
| Waterloo Univ.(2018) [25] | LSTM+3DCNN | Surface Code | 회로수준 | ~7.11×10 | 5 | N/A |
| Leiden Univ./TU Delft(2019) [26] | RNN/LSTM | Color Code | 회로수준 | ~0.0023 | 7 | N/A |
| UdeS(2019) [27] | BP | Toric Code | i.i.d. X&Z | ~0.07 | 10 | N/A |
| Dusseldorf Univ.(2019) [28] | FFNN(+MWPM) | Toric Code | 탈분극 | N/A | 7 | O(MWPM) |
| TU Delft(2020) [29] | DL+RG | Toric Code | i.i.d. 비트반전 | ~0.103 | 64 | > O(RG) |
| UCM(2020) [30] | MLP+CNN | Semion Code | 탈분극 | ~0.105 | 13 | N/A |
| Melbourne Univ.(2021) [31] | CNN(+HDRG) | Surface Code | 탈분극, 편향 | 0.138 | 1,025 | > O(HDRG) |
| Cologne Univ.(2021) [5] | ML(+UF/MWPM) | Toric Code | 탈분극 | 0.167 | 255 | O(UF) |
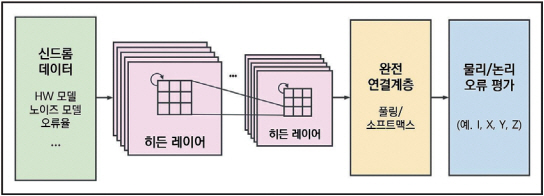
신경망 모델을 사용하는 기술 분야는 학습 데이터 집합의 구축이 매우 중요하다. 신경망 알고리즘 기반 오류 복호기의 경우에는 학습을 위한 데이터를 양자 노이즈 모델 기반의 모의 생성기를 통해 생성하거나 실제 물리 양자머신 시스템으로부터 수집하여 생성할 수도 있다. 여기에 덧붙여서 강화학습(RL: Reinforcement Learning) 기술을 생성된 학습 데이터에 적용해 학습용 데이터를 개선[32]하기도 한다. 한편 양자 컴퓨팅 시스템에서 논리 큐비트 부호화를 위한 코드 크기가 증가함에 따라 신드롬 발생 경우의 수가 기하급수적으로 늘어나고 학습 비용도 동시에 상승하는 문제를 극복하기 위해 신경망 기반 오류 복호기의 학습에 사용되는 데이터를 압축하거나 축소하는 연구도 시도되고 있다. 한 가지 예로 오류정정코드의 양자 데이터에 대칭성(Symmetry) 적용이 가능한 경우 학습 전처리 단계에서 학습 데이터를 축소하거나 확대하여 학습과 추론의 수행[28]을 효과적으로 처리하는 것이 가능하다.
많은 연구에서 신경망 알고리즘을 기존의 고전 복호화 알고리즘과 결합하여 정확성과 확장성 특성을 동시에 만족하는 양자 오류 복호기를 구성하는 방법을 제안하였다. 다양한 자료에서 이런 혼용 복호화 방식을 고수준/저수준 복호기(High/Low-level Decoder), 계층 복호기(Hierarchical Decoder) 혹은 이단계 신경망 복호기(Two-stage NN Decoder) 등으로 명명한다.
2021년 쾰른대학[5]에서는 d=255 규모의 2D 및 3D Toric Code에서 UF 복호기와 FFNN 복호기를 결합한 이단계 신경망 복호기를 제안하였다. 복호화 프로세스를 지역 오류 수정을 위한 신경망 전처리와 UF 복호기를 사용한 광역 오류 수정의 두 단계로 나누어 처리함으로써 UF 복호기만을 사용할 때 보다 초기 오류율을 2배 이상 줄여 후속 UF 복호화 단계의 처리 속도를 높이고 확장성과 논리 정확성 향상을 가져왔다.
향후 주의 깊게 살펴볼 또 다른 연구 방향으로는 메모리 공간 사용 효율을 극대화하기 위한 이진연산 CNN 기술이나 NEAT(NeuroEvolution of Augmenting Topologies) 기술을 적용한 사례가 있다. 또한, 작은 코드거리로 인코딩된 데이터를 학습하여 큰 코드거리의 오류 복호화 처리를 가능하게 하는 전이학습(TF: Transfer Learning) 기술[22]도 주목할 만하다.
일반적으로 신경망 기반 오류 복호기는 입력과 무관하게 추론 시간이 일정하고 높은 추론 정확성을 달성할 수 있는 장점이 있다. 또한, 병렬 처리 구조를 갖고 있어 파이프라이닝 기법 적용이 가능해 하드웨어 최적화에 적합한 측면도 있다. 그러나 신경망 기반 복호기는 아직은 대규모 큐비트 환경에서 연구 사례가 많지 않다. 다만 최근에는 제한적이 지만 d=255나 d=1,025 크기의 시스템 규모에서 신경망 기반 오류 복호기가 좋은 오류 임계값을 달성한 연구가 다수 등장하고 있어 FTQC 환경과 대규모 양자 컴퓨팅을 위한 확장성 관점에서 지속적으로 많은 기대를 받고 있다. 이후 절에서는 주요 신경망 알고리즘별로 상세한 오류 복호기의 연구 사례를 살펴본다.
1. FFNN 기반 신경망 오류 복호기
순방향신경망(FFNN: Feed-Forward NN)은 입력 계층에서 출력 계층 방향, 즉 순방향으로만 연산이 전개되는 가장 기본적인 신경망 모델이다. 최초의 FFNN 신경망 기반 복호기는 TU Delft[22], 워털루 대학[23], 예일대학[24]의 연구 사례가 있다. 본고에서는 TU Delft의 복호기 연구를 중심으로 살펴본다.
TU Delft 복호기는 E=S·P·L 분해기법을 사용하여 해당 오류를 L을 위한 분류 문제로 전환하고 FFNN 신경망을 통해 논리 수준 오류로 인식한다. 학습 데이터 집합은 단일 물리 오류 확률에서 직접 샘플링하여 MWPM 오류 임계값 수준으로 생성한다. d≤7의 표면코드는 가능한 전체 신드롬을 대상으로, d>7 이상의 표면코드는 최대 106개의 제한적 신드롬을 대상으로 학습 데이터를 샘플링한다. 이 연구에서 TU Delft는 양자 컴퓨터에서 발생하는 다양한 오류를 대상으로 FFNN 기반 신경망 복호기의 성능을 각 노이즈 모델에 대해 여러 코드거리로 나누어 분석하였다. 또한, 복호화 문제를 분류 문제로 변환 처리하기 위해 물리 수준의 오류 보정을 위한 저수준 복호기(LLD: Low-Level Decoder)와 논리 수준 오류 보정을 위한 ML 기반 고수준 복호기(HLD: High-Level Decoder)를 활용하였다. 이런 방식으로 TU Delft 복호기는 고전 알고리즘 오류 복호화 방식 대비 처리 지연 문제를 상당히 해소하였을 뿐만 아니라 오류 복호화 처리 성능도 MWPM 임계값 수준에 근접하였다. 균일한 추론 시간, 코드거리에 비례한 선형적 처리 시간의 장점을 보여 주고 있는 것이다. 그러나 학습 데이터 집합이 커질수록 단순 FFNN 알고리즘 기반 복호기는 학습 비용이 큰 폭으로 증가한다는 점도 분명히 하고 있다.
2. CNN 기반 신경망 오류 복호기
합성곱신경망(CNN: Convolutional NN)은 영상, 이미지 등의 처리에 최적화된 신경망 모델이다. 그림 2와 같이 오류 복호기는 I, X, Y, Z 오류 상태를 분류하게 되므로 합성곱신경망의 적용이 자연스러울 수 있다. CNN 기반 신경망 오류 복호기 기술 사례는 대규모 시스템을 위한 확장성이 고려된 멜버른대학의 연구[31]를 중심으로 살펴본다.
멜버른대학의 연구는 결함홀(Defect Hole)을 갖는 정방형 표면코드상에서 균질한 탈분극 노이즈, 이질적 공간분포 노이즈 및 편향성 노이즈와 같은 다양한 무작위 분포를 갖는 학습 데이터를 기반으로 학습된 오류 복호기의 성능을 검증하였다. 이 연구는 d=1,025 초과 논리 큐비트 형상에서도 작동하는 것으로 평가됨에 따라 전용 하드웨어에서도 큐비트 일관성 시간에 상응하는 O(μsec) 수준의 표면코드 복호화를 제공할 수 있을 것으로 전망되었다. 이 연구에서 구현된 오류 복호기는 지역적으로 오류를 신경망 알고리즘으로 복호화하고 광역적으로는 HDRG(Hard-Decision RG) 고전 알고리즘을 적용하는 이단계 신경망 복호화 방식을 사용하였다.
멜버른대학은 학습할 오류 데이터 유형을 독립된 X/Y/Z 오류, 다수가 인접한 X/Z 오류, 경계선상의 X/Z 오류 등 10가지의 오류 패턴으로 정의하고, 오류 인식률을 낮추는 특정 오류 패턴을 경험적 방식을 적용하여 다른 형태로 변형함으로써 학습 데이터의 오류 인식률을 향상시키도록 개선하였다. 오류 복호화 과정에서 지역 오류를 정정하기 위해 신경망 복호기를 잔여 오류가 10% 이하가 될 때까지 반복 실행하며, 넓은 영역에 걸쳐 있어 학습이 어려운 광역 오류는 대규모 코드거리에서 비교적 신속한 처리가 가능한 HDRG 알고리즘을 통해 오류정정을 진행한다.
이런 방식의 지역 오류정정을 지원하는 신경망 기반 복호화 단계는 원칙적으로 코드거리에 무관한 실행 시간 처리가 가능하지만, 광역 수준에서 최적 성능의 복호기를 제공하기 위해 지역 복호기를 반복 수행해야 하므로 처리 지연이 발생할 수 있다. 또한, 보조 큐비트 측정 오류 발생 상황에서 오류 복호기의 정상 작동 여부나 저지연성, 확장성 등의 복호화 성능 특성의 충족 여부도 아직 명확하지 않다.
3. RNN 기반 신경망 오류 복호기
순환신경망(RNN: Recurrent NN)은 시간적 순서를 갖는 시계열 데이터 처리 문제에 적합한 신경망 모델이다. 순환신경망은 학습과 추론에 더 많은 계산량이 요구되나 이전 순회 정보를 활용하여 다음 오류를 예측하므로 오류의 시간적 특성을 활용해 판단할 수 있는 장점이 있다.
2018년 워털루대학의 연구[25]는 저수준 복호기로 LUT(Look-Up Table) 또는 PED(Pure Error Decoder)를 고수준 복호기로, RNN 또는 3차원 CNN 알고리즘 복호기를 대상으로 여러 복호기 조합에 따른 성능 분석을 진행하였다. 본고에서는 워털루대학이 조합 복호기에 사용한 RNN 기반 복호기에 대해서 살펴본다.
RNN 기반 복호기는 측정 오류를 포함한 d=3 또는 d=5 표면코드를 대상으로 각각 X/Z 신드롬을 담당하는 격리된 2개의 LSTM(Long Short Term Memory) 네트워크로 구성된다. 각 LSTM 네트워크는 신드롬 시퀀스를 저수준 복호기의 출력과 함께 학습 데이터로 입력받는다. 이를 통해 측정 오류가 있는 신드롬에 대해 저수준 복호기의 오류정정 과정이 발생시키는 논리오류를 복원할 수 있도록 학습된다. 해당 연구는 LUT 또는 PED를 사용한 저수준 복호기와 RNN 또는 CNN 기반 고수준 복호기를 조합한 이 단계 신경망 복호기의 성능 및 고려사항을 조합별로 분석하여 특성을 제시하고 있어 고수준/저수준 복호기에 대한 의미 있는 연구 참조 사례로 보인다.
4. RL 기반 신경망 오류 복호기
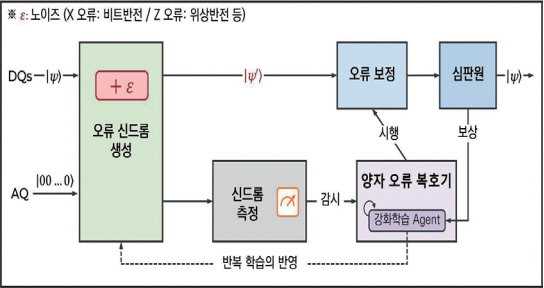
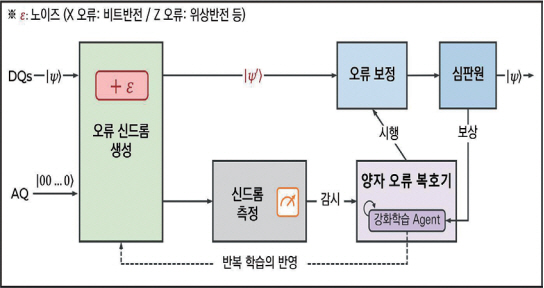
강화학습(RL: Reinforcement Learning)은 순차적 의사결정 문제를 해결하는 방법으로 시스템의 특정 상태는 바로 이전 상태에 의해서만 영향을 받는다는 전제에 의해 MDP(Markov Decision Process)로 환경 전이함수를 이용한다.
효과적인 양자 오류정정 목표를 달성하기 위해 그림 3과 같이 복호화의 시행과 착오 개선 과정에서 환경과 상호작용하는 강화학습 에이전트(RL Agent)가 재학습을 통해 오류 복호기의 성능을 개선한다. 또한, 강화학습 기법에서는 학습 데이터를 신경망 네트워크 자체를 사용하여 생성할 수 있는 특징이 있다. 표 5에서는 현재까지 강화학습 기법이 적용된 신경망 기반 복호기 연구 사례 현황을 간략히 정리하였다.
표 5 강화학습 기반 오류 복호기 연구 사례
| 사례 | 오류정정부호 | 노이즈 모델 | 오류 임계값 | dmax | 계산 복잡도 |
|---|---|---|---|---|---|
| Innsbruck Univ./Leiden Univ./Konstanz Univ./MS(2018) [32] | Surface Code | i.i.d. | N/A | 3, 5 | O(UF) |
| MPL(2018) [33] | Surface Code | 비트반전, 상관 노이즈 | N/A | N/A | N/A |
| Gothenburg Univ.(2019) [34] | Toric Code | i.i.d. 비트반전 | ~0.1 | 7 | >> O(n) (추정) |
| Chalmers Univ.(2019) [35] | Toric Code | 탈분극 | N/A | 5, 7 | > O(MWPM) |
| Chalmers Univ.(2020) [36] | Toric Code | 탈분극 | ~0.165 | 7(9) | >> O(n) (추정) |
| UAB(2020) [37] | Toric Code | i.i.d. 비트반전 | 0.103 | 9 | > O(MWPM) |
| FU Berlin/Copenhagen Univ.(2020) [38] | Surface Code | i.i.d. 비트반전 & 탈분극 | N/A | 5 | >> O(n) (추정) |
| Toulouse Univ./Copenhagen Univ.(2021) [39] | Toric Code | 비트반전 | N/A | 7(11) | > O(MWPM) |
현재 강화학습 기반의 오류 복호기 연구는 유럽연구기관을 중심으로 수행되고 있으나 아직 기술 완성도가 높지 않으며 많은 연구가 오류 임계값 자체를 제시하지 못하는 상황이다. 다만 소수의 연구[36]에서 작은 코드거리 규모에서만 MWPM과 같은 고전 알고리즘 대비 우수한 임계값을 달성한 수준이다.
정보 레이블이 달린 학습 데이터를 사용하여 높은 처리 학습량을 보이는 지도학습(Supervisor Learning)과 달리, 강화학습 기반 신경망 복호기는 학습 데이터를 네트워크 자체를 사용하여 생성하므로 코드거리가 커질수록 학습 수렴 속도가 상당히 제한된다. 이를 극복하기 위한 방법으로 하드웨어 자원 활용도를 높이면서 학습시간을 단축하기 위해 독립적으로 환경을 탐색하고 공유 메모리 버퍼를 채우는 분산 강화학습 기법[40]이 연구되고 있다. 다만, 이 방식은 큰 네트워크 크기로 인해 순방향 전파에 필요한 비용이 상승하여 오류 복호화 속도가 제한될 수 있다. 따라서 학습시간 단축과 복호화 속도 제한 문제에 대한 해결이 강화학습 연구의 핵심이다. 심층 잔류 신경망(Residual NN)[41]은 가장 적합한 네트워크 유형과 깊이를 체계적으로 탐색하는 것으로 d=9에서 학습 수렴 속도를 개선하는 것으로 알려져 있다. 또한, 복호기의 성능을 개선하기 위한 유망한 방법은 개념적으로는 단순하지만, 비효율적인 Q 학습 방법을 개선하는 것이다. 이 접근법의 단점은 복호화 과정 중에 추가적인 계산이 필요하다는 점이다. 이것을 극복하기 더 간단한 접근 방식은 재강화(RE-INFORCE) 알고리즘[42]과 같은 정책 기반 알고리즘을 사용하는 것이다. 이 알고리즘은 액션값을 계산하거나 트리 검색을 수행하지 않고 정책을 직접 최적화한다.
강화학습기반 복호기 성능에 대한 또 다른 중요한 요소는 보상체계다. 일반적으로 경험적 방법을 사용하여 보정 체인의 길이를 최소화하는데 이는 오류율이 0에 근접한 제한적인 경우에만 최적 성능을 갖는다. 더 큰 오류율과 편향된 노이즈에 대한 성능을 개선하기 위해 현재 각 신드롬에 대한 오류 체인의 몬테카를로(Monte Carlo) 생성 분포에 기반한 보상체계를 모색하는 연구[43,44]도 진행 중이다.
Ⅴ. 하드웨어 기반 양자 오류 복호기
이 장에서는 극저온 운영 환경에서 전력효율과 실시간 실행을 고려한 하드웨어 기반 양자 오류 복호기의 연구를 정리한다.
하드웨어 기반 큐비트 오류 보정을 위해 사전 계산 정보를 활용하는 LUT 방식 오류 복호기는 d=5 수준 이하에서만 정상 동작이 가능하여 코드 규모 확장성에 제약이 따른다. 또한, 모든 신드롬 측정 후에 복호화 과정을 진행하는 기존 batch QEC 기법은 코드거리의 세제곱에 비례하는 방대한 오류 정보가 사용되므로 오류정정 처리 지연을 가중시켜 오류 처리가 지속적으로 누적될 가능성을 내포한다. 이런 경우 대규모 저장 메모리를 사용하므로 복호기 구현에 필요한 하드웨어 비용도 그에 따라 상승한다. 이를 해결하기 위해 신드롬 측정과 복호화를 동시에 수행함으로써 신드롬 측정 오류에 효과적으로 대응하는 online QEC 기법이 제안되었다. 이 방식은 표면코드의 측정 신드롬을 신속히 해독함으로써 오류 처리 누적을 피할 수 있고 코드거리와 무관하게 일정한 양의 메모리만으로 하드웨어 방식 오류 복호기를 구현하는 것이 가능하다. 주요 연구 사례를 중심으로 하드웨어 면적, 전력 소모량, 처리 지연 시간 등을 간단히 비교해 보면 표 6과 같다.
표 6 주요 극저온 환경 하드웨어 복호기의 메트릭 비교
| 복호기 | NISQ+ [46] | PED+NN [49] | QULATIS [51] | NEO-QEC [52] | Clique [53] |
|---|---|---|---|---|---|
| 플랫폼 | SFQ | Cryo-CMOS | SFQ | SFQ | SFQ |
| 측정 오류 | - | - | ✓ | ✓ | ✓ |
| 격자 연산 | - | - | ✓ | ✓ | - |
| 면적(mm2) | 369 | 10 | 16.4 | N/A | 14.4 |
| 전력(µW) | 3,780 | 20,000 | 417.4 | 614.9 | 99 |
| 지연(ns) 최대/평균 | 19.2/3.8 | 28 | 82/2.12 | N/A | 0.24 |
※ 면적, 전력 소비 및 지연은 d=9 논리 큐비트 기준임.
CMOS: Complementary Metal-Oxide-Semiconductor
SFQ: Single Flux Quantum
출처 Reproduced from [45], CC BY 4.0.
표 7에서는 최근 진행된 초전도 환경에서 저전력, 실시간 실행을 지원하는 대표적인 하드웨어 방식 오류 복호기 연구 사례 현황을 간략히 정리하였다. 상세 내용은 이후 각 절에서 자세히 살펴본다.
표 7 하드웨어 기반 오류 복호기 연구 사례
| 사례 | 연구기관 | 특징 | 달성치 |
|---|---|---|---|
| NISQ+ [46] | Chicago Univ./USC(2020) | AQEC(Approximate QEC) 방법 / MWPM에 근사 / 확장성을 위한 SFQ 모듈의 2차원 배열 / 전력 절감을 위한 ERSFQ(Energy-efficient Rapid SFQ) 라이브러리 / (문제점) 리소스 병목 현상, 확장성 제약, 측정 오류 반영 미흡 | d=3, 5, 7, 9 / 평균 지연: 20ns / 최초 SFQ 칩 |
| QECOOL [47] | Tokyo Univ./NTT(2021) | 오류정정 주기 단축을 위한 3D 격자 기반의 온라인 QEC / 극저온 환경에서도 작동 / 2,500 논리 큐비트 / 오류 임계값을 소폭 낮춰 확장성 향상 / 면적 효율적인 소형 레지스터 기반 분산 구조 / NISQ+ 이상의 성능 달성(지연 지표는 제외) | d=5, 7, 9, 11, 13 / SFQ |
| LILLIPUT [48] | Google(2021) | 단기 양자 HW를 위한 실시간 복호화 / 가장 가능성이 높은 오류 이벤트 데이터만 저장하여 3레벨 압축 LUT(CLUT) 유지 / 백만 번의 무작위 시도를 통해 몬테카를로 시뮬레이션 인프라 검증 | d=3, 4, 5 / 평균 지연: 21ns (최대, ≤42ns) |
| PED+NN [49] | TU Delft(2022) | 저수준 PED 복호기와 고수준 FFNN 복호기로 2단계 신경망 복호기 구현 / 복호화 성능(오류율, 연산 지연)과 HW 비용(면적, 전력) 간의 절충 평가 / 모든 오류 체인 등거리 라우팅 최소화 및 회전 대칭성 활용으로 빠른 HW 복호화 달성 | d=3, 5, 7, 9 / 지연: ASIC (< 30ns), FPGA (< 90ns) 극저온 Cryo-CMOS |
| AFS [50] | Georgia Tech/Caltech/MS(2022) | 저장공간 및 대역폭 요구 스케일링과 관련한 도전 요인 분석 / 측정 오류 반영 / CDA(Conjoined Decoder Architecture)를 사용하여 저장소 부하 경감 / 희소 데이터 특성을 활용하여 신드롬 데이터 30배 압축 | d=11 / 평균 지연: 42ns, 99.9%의 지연: 150ns |
| QULATIS [51] | Tokyo Univ./NTT(2022) | 실용적인 복호화 회로로 격자 연산을 지원하는 온라인 QEC 알고리즘 / 병합 과 분할을 위해 유연한 경계 제어 / NISQ+ 및 QECOOL보다 향상된 확장성 / MWPM 복호기보다 낮은 성능 | d=5, 7, 9, 11 / SFQ & Cryo-CMOS |
| NEO-QEC [52] | Tokyo Univ./NTT(2022) | 합성곱신경망과 기존 온라인 그리드 복호기를 결합하여 측정 오차가 있는 표면 코드 및 격자 연산을 복호화하기 위한 신경망 기반 온라인 QEC 알고리즘 | d=5, 7, 9, 11, 13 / SFQ |
| Clique [53] | Chicago Univ./USC/IBM(2023) | SFQ 로직 극저온 도메인을 위한 경량 복호기 / 오프칩 복호화 대역폭(BW) 할당을 위한 통계적 신뢰도 기반 기법 / BTWC(Better Than Worst-Case) 복호화를 사용하여 70~99% 이상의 오프칩 대역폭 제거 / d=9에서 NISQ+ 대비 15~37배 자원 부하 경감 / 정확성과 처리 성능을 위한 온오프칩 2단계 분리 설계 | d=3, 5, 7, 9, 11 / SFQ |
| Helios [54] | Yale Univ. (2023) | 분산형 UF 복호기 / FPGA를 사용한 확장형 구조 / 병렬 컴퓨팅 자원을 하이브리드 트리-그리드 구조로 구성한 확장형 아키텍처 / 평균 10.7 주기 (AFS 168주기, QECOOL 41주기) | d = 7 (~ 15) / 평균 지연: 120ns |
1. NISQ+
2020년 시카고대학과 USC 연구진은 NISQ(Noisy Intermediate-Scale Quantum) 환경에서 더 많은 양자 계산이 가능하도록 하는 근사적 양자 오류 수정(AQEC: Approximate QEC) 기법[46]을 제안하였다. 이 기법은 정확성을 일부 희생해서 오류 복호화를 신속하게 수행할 수 있는 근사 표면코드 복호기로서 SFQ(Single Flux Quantum) 합성 도구를 사용하여 면적과 전력 상황이 제한적인 극저온 냉각 환경에서 복호화를 수행할 수 있는 기능이 제공된다. 또한, 각 큐비트당 하나의 복호기 모듈을 사용하는 확장형 모듈식 구조를 기반으로 최대 20ns 내에서 실시간 오류정정 성능을 제공한다. NISQ+는 높은 정확성과 낮은 지연 시간을 달성하지만 오류가 배제된 완벽한 신드롬 측정을 가정하므로 실제 신드롬 측정 시 오류가 발생하는 경우 큐비트의 정확성이 심각하게 저하될 수 있다. 이 연구의 의의는 d=3, 5, 7, 9 경우에 대해서 구현된 최초의 SFQ chip 기반 복호기라는 점이다.
2. LILLIPUT
2021년 구글 양자AI팀에서 제안한 LILLIPUT(Lightweight Low Latency Look-Up Table) 복호기[48]는 단기 양자 하드웨어에서 ns급 오류정정 처리 지연과 실시간 복호화를 제공한다. 게이트 연산 및 측정을 포함한 양자 하드웨어의 모든 작업에서 결함 내성을 갖는 모델을 사용하며 400ns 내의 성능을 만족시킨다. 또한, LUT를 위한 메모리 사용량도 오류 신드롬 데이터의 희소성 특징을 활용해 성능 저하 없이 107배까지 줄인 후, d=3, 4, 5에 대해서 Monte Carlo 시뮬레이터를 이용하여 100만 개의 무작위 시행에 대해 검증하였다. 그러나 Overlapping recovery 기법에서 착안된 구글의 실시간 복호기인 LILLIPUT는 LUT 확장성에 근본적인 한계가 있다. 이와 관련하여, Riverlane-UCL[55]과 Alibaba[56]의 최신 연구는 병렬 처리 복호화 기법을 이용하여 시스템의 저지연성과 확장성을 개선함으로써 데이터 백로그 문제를 해소한 사례다.
Riverlane-UCL은 병렬 윈도우 복호화 파이프라인 구조를 적용하여 다항적 확장 가능한 실시간 복호화 방안을 제시하였다. 유사한 시기에 Alibaba도 병렬 처리를 통해 보정 일관성(Correction Consistency) 문제를 해결하고 표면코드에 빠른 고전적 처리를 제공하는 슬라이딩 윈도우 복호기(Sliding Window Decoder) 체계를 도입하였다. 이 방식은 시공간에서 신드롬을 시간 방향을 따라 겹치는 윈도우로 나누고 내부 복호기(Inner Decoder)로 병렬 복호화를 진행한다. 이 기법은 처리 성능이 낮은 내부 복호기(예: MWPM, UF 등)를 사용하더라도 코드 규모가 증가함에 따른 복호화 확장 처리 성능 문제를 해결할 수 있음을 보여 주었다.
3. PED+NN
TU Delft는 면적과 전력 사용량에 대한 최소 하드웨어 구현을 유지하면서 높은 복호화 성능을 제공하는 것을 목표로 저수준 복호기 PED(Pure Error Decoder)와 FFNN 기반 논리 오류 보정용 고수준 복호기로 구성된 이단계 신경망 복호기[49]를 제안하였다. 이 연구에서는 짧은 코드거리의 표면코드를 대상으로 하는 완전 연결 FFNN 기반 복호기에 대한 공간탐색 방법을 제시하였다. 이 방식은 ASIC(Application Specific Integrated Circuit) 설계 시 30ns 미만, FPGA(Filed-Programmable Gate Array) 구현 시 90ns 미만의 결과를 얻었으며, 이는 하드웨어 기반 신경망 복호기가 다른 최신 복호화 알고리즘에 필적하는 높은 복호화 성능을 달성할 수 있음을 제시하였다.
4. AFS
Georgia tech, Caltech, Microsoft 등 미국 산학 협업으로 진행된 복호기 연구는 기존 선행 복호화 연구가 정확성에만 초점을 맞춘 것과는 달리, 수천 개의 큐비트를 대상으로 하는 대규모 시스템에서 오류정정을 수행할 때 필요한 저장 및 대역폭 자원의 확장성 문제를 분석하였다. 이 연구의 결과로 수백 개의 논리 큐비트 규모에서 확장 가능한 복호화 구조인 AFS(Accurate, Fast, and Scalable Error-Decoding)[50]를 제안하였다. AFS는 UF 알고리즘을 기반으로 3단계 파이프라인 설계를 사용하는 하드웨어로 구현된다. AFS는 SFQ 기반 하드웨어 복호기에 비해 훨씬 높은 정확성(물리 오류율 10-3에 대해 논리 오류율 6×10-10)과 낮은 복호화 지연 시간(평균 42ns)을 제공하며, 신드롬 측정 오류에도 비교적 견고한 특징이 있다. 이 연구에서는 여러 복호화 유닛을 공동으로 결합 설계하는 결합 복호화 아키텍처(CDA: Conjoined-Decoder Architecture)를 도입하여 마이크로 아키텍처의 하드웨어 크기(예: 저장소 부하 70%)를 상당 부분 줄였다. 또한, 신드롬의 데이터 희소성을 활용해서 데이터를 압축함으로써 입력 대역폭 요구량을 30배까지 개선하였다.
5. NEO-QEC
도쿄대학, NTT 등 일본 산학 협업으로 진행된 NEO-QEC 복호기 연구[52]는 신드롬 측정 오차가 있는 표면코드와 격자 연산(Lattice Surgery)을 복호화할 수 있는 높은 정확성, 저지연, 저전력 효율성을 갖는 신경망 기반 온라인 복호기를 제안하였다. 이 복호기는 멜버른대학의 CNN 기반 디코더를 확장하여 정확성 저하가 중간 정도인 binary CNN 기술을 적용하였고, 에너지 효율이 좋은 ERSFQ(Energy-efficient Rapid SFQ) 기반 디지털 회로로 복호기용 NPU(Neural Processing Unit)를 설계하였다. 그리고 SPICE 레벨 시뮬레이션을 통해 그 성능을 평가하였다. NEO-QEC는 단일 논리 큐비트 유휴 연산과 코드거리가 d=13인 격자 연산의 최소 동작에 대해 복호기 성능을 평가한 결과 각각 2.3%, 1.3%의 임계값을 달성하였다. 이 결과는 MWPM 복호기보다는 여전히 낮고, QECOOL 복호기[47]보다는 모든 코드거리에서 높은 성능을 가지고 있는 정도다. NEO-QEC도 경량 binary CNN 기술을 사용한 3D 기반 이단계 신경망 복호기로 극저온 환경에서 짧은 지연 시간과 저전력 달성에 의미를 둘 수 있다.
6. Clique
시카고대학, USC, IBM은 90% 이상이 양자 오류 패턴이 반복되거나 극히 드물게 발생하는 단순 오류라는 분석 결과를 바탕으로 상온의 오프칩 대역폭을 70~99% 이상 제거하면서도 복호기 성능을 크게 저하시키지 않는 Clique 복호화 인프라[53]를 제안하였다. Clique은 첫 번째 단계는 극저온 환경에서 간단한 오류 시나리오 처리가 가능한 경량 온칩 SFQ 로직 복호기로 구성하고, 두 번째 단계는 상온 환경에서 발생 빈도는 낮으나 복잡도가 높은 오류 시나리오를 처리하는 고성능 복호기로 구성함으로써 기존 저온과 상온 장치 간에 필요하였던 입출력 부하를 10~100배 감소시켜 시스템 대역폭 병목을 개선하였다. 또한, 시스템 전체적으로 극저온 환경의 SFQ 로직 복호기가 상당히 단순하여 자원 활용 측면에서 기존 온칩 광역 SFQ 기반 복호기에 비해 15~37배의 소요자원 감소 효과를 달성하였다.
7. Helios
UF 복호화 알고리즘은 MWPM 알고리즘보다 계산 복잡도가 낮고 분산 버전 구현이 용이하다는 장점이 있다. 2023년 예일대학은 분산 버전의 UF 복호화 알고리즘 기반 하이브리드 트리-그리드 구조를 적용해 확장 가능한 복호화 아키텍처인 Helios[54]를 공개하였다. Helios는 FPGA 구현을 사용하여 분산형 UF 복호기가 O(d3) 병렬 컴퓨팅 자원이 주어졌을 때 코드거리 d에 대해 준선형 평균 계산 복잡도를 갖는다는 것을 실증하였다. 또한, 자일링스의 사이클 정확성 시뮬레이터를 사용하여 물리 오류율 0.1%를 갖는 현상학적 노이즈 모델에서 측정 라운드당 복호화 시간이 양자 오류 복호기로서는 처음으로 코드거리(d≤7)가 증가하여도 감소함을 보였다. 이 결과는 일반적인 복호기 구현에 있어서 코드거리가 증가함에 따라 기하급수적으로 발생하는 백로그 증가 없이 임의 코드거리의 양자 오류도 복호화할 수 있음을 보여 준 사례로 의미가 있다.
Ⅵ. 결론
양자 컴퓨팅이 NISQ 단계를 거쳐 내결함성 단계로 진입하기 위한 핵심 기술 분야가 양자 오류정정이다. 최근 양자 오류 복호기 연구는 정확성(Accuracy), 저지연성(Speed), 확장성(Scalability)의 기본 요구사항을 충족하는 복호화 알고리즘과 함께 극저온, 저전력 등의 다양한 한계 환경에도 능동적으로 대응하는 유연성(Flexibility)을 갖춘 복호화 기술에 대한 연구가 동시에 진행되고 있다. 본고에서는 정확성에 강점을 갖는 고전 오류 복호기와 저지연성과 확장성에 강점을 갖는 신경망 기반 오류 복호기의 연구 동향과 함께 유연성을 고려한 하드웨어 기반 오류 복호기의 최신 연구 사례들을 분석하였다.
고전 복호기 사례에서는 MWPM, UF, TN 알고리즘의 기능 개선이나 병렬 분산 연구 등이 주목되는 사례였다. 신경망 기반 복호기 사례에서는 정확성과 저지연성 달성에 목표를 두고 다양한 머신러닝 기법을 적용하여 다수의 의미 있는 결과를 얻었다. 실제 시스템에 적용을 위한 최적 복호기 구현을 위해서 복호화 정확도나 저지연성뿐만 아니라 하드웨어 한계 환경을 유연하게 반영해 확장성도 고려한 사례도 다수 확인된다. 또한, 양자 오류 복호기는 처리 시간 지연 한계를 만족해야 하는 저지연성 시스템 요구로 FPGA나 ASIC 기반의 하드웨어 구현 복호기 연구 사례가 있으며, 극저온 환경을 위한 저전력 시스템 요구도 있어 Cryo-CMOS를 사용한 온칩 복호기 연구 사례도 찾아볼 수 있었다.
최종적으로 10-15 수준의 오류율을 목표로 하는 FTQC는 모든 하드웨어 요소에서 발생하는 현실적인 노이즈 모델에 대한 처리를 고려하고 있으며, 해당 연구 영역의 도전성이 높아 다수 산학연구기관의 상호 협력이 활발히 이루어지고 있다. 양자 오류 복호기는 단시간에 달성할 수 있는 크기의 문제가 아니므로 기존 연구를 향후 하드웨어, 다양한 코드 규모, 또는 오류 상황에 유연하게 적용할 수 있도록 고려하는 것도 중요한 연구 과제가 된다. 또한, 실시간 복호기의 최근 연구 사례를 참조하여 복호화 처리 병렬성 증대, 복호화 과정에 필요한 입출력 대역폭 저감, 신경망 모델의 학습을 고려한 데이터 압축 및 구현 복호기의 저전력성 만족 등의 요소를 균형있게 조율하는 연구도 동시에 고려되고 있다.
요약해 보면, 향후 기대 수준의 FTQC를 구현하기 위해 미래 양자 오류 복호기 분야는 신경망 알고리즘 및 하드웨어 온칩 구현 등을 포함하여 최신 기법들을 지속적으로 개선하고 적용하여 오류 복호기에서 시급하게 필요한 품질 요구사항들을 순차적으로 달성해 갈 것으로 예상한다.
용어해설
NISQ 아직 내결함성이 충분히 발전하지 않았거나 양자 우위를 달성할 만큼 충분히 크지 않은 규모의 양자 컴퓨팅
FTQC 양자 오류보정이 적용된 양자 컴퓨팅
QEC 양자정보 처리용 큐비트에 발생한 양자 오류를 정정하는 기술
QED 양자 오류정정부호에서 측정된 오류 신드롬으로부터 오류 위치를 추론하는 기술
약어 정리
AQEC
Approximate QEC
ASIC
Application Specific Integrated Circuit
CDA
Conjoined-Decoder Architecture
CMOS
Complementary Metal-Oxide-Semiconductor
CNN
Convolutional NN
ERSFQ
Energy-efficient Rapid SFQ
FFNN
Feed-Forward NN
FPGA
Field-Programmable Gate Array
FTQC
Fault-Tolerant Quantum Computing
HDRG
Hard-Decision RG
HLD
High-Level Decoder
IRMWPM
Iteratively Rewighted MWPM
LLD
Low-Level Decoder
LSTM
Long Short Term Memory
LUT
Look-Up Table
MDP
Markov Decision Processing
MERA
Multi-scale Entanglement Remormalization Ansatz
MLD
Maximum Likelihood Decoding
MWPM
Minimum Weight Perfect Matching
NEAT
NeuroEvolution of Augmenting Topologies
NISQ
Noisy Intermediate-Scale Quantum
NN
Neural Network
NPU
Neural Processing Unit
PED
Pure Error Decoder
QEC
Quantum Error Correction
QED
Quantum Error Decoding
RG
Renormalization Group
RL
Reinforcement Learning
RNN
Recurrent NN
SC
Surface Code
SDRG
Soft-Decision RG
SFQ
Single Flux Quantum
TF
Transfer Learning
TN
Tensor Network
UF
Union-Find
P. Das et al., "A scalable decoder micro-architecture for fault-tolerant quantum computing," arXiv preprint, CoRR, 2020, arXiv: 2001.06598.
D. Poulin, "Optimal and efficient decoding of concatenated quantum block codes," Phys. Rev. A, vol. 74, no. 5, 2006, article no. 052333.
K. Meinerz et al., "Scalable neural decoder for topological surface codes," Phys. Rev. Lett., vol. 128, 2021, article no. 080505.
R.E. Tarjan, "Efficiency of a good but not linear set union algorithm," J. ACM, vol. 22, no. 2, 1975, pp. 215-225.
J.W. Harrington, "Analysis of quantum error-correcting codes: Symplectic lattice codes and toric codes," Ph.D. Thesis, California Institute of Technology, 2004.
N. Delfosse and N.H. Nickerson, "Almost-linear time decoding algorithm for topological codes," Quantum, vol. 5, 2021.
G. Duclos-Cianci and D. Poulin, "Fast decoders for topological quantum codes," Phys. Rev. Lett. vol. 104, 2010, article no. 050504.
A.G. Fowler, "Minimum weight perfect matching of fault-tolerant topological quantum error correction in average O(1) parallel time," Quantum Info. Comput., vol. 15, 2015, pp. 145-158.
O. Higgott, "PyMatching: A python package for decoding quantum codes with minimum-weight perfect matching," ACM Trans. Quantum Comput., vol. 3, no. 3, 2022, pp. 1-16.
O. Higgott et al., "Sparse blossom: Correcting a million errors per core second with minimum-weight matching," arXiv preprint, CoRR, 2023, arXiv: 2303.15933.
Y. Yuan et al., "A modified MWPM decoding algorithm for quantum surface codes over depolarizing channels," arXiv preprint, CoRR, 2022, arXiv: 2202.11239.
N. Delfosse, "Hierarchical decoding to reduce hardware requirements for quantum computing," arXiv preprint, CoRR, 2020, arXiv: 2001.11427.
H. Anwar et al., "Fast decoders for qudit topological codes," New J. Phys., vol. 16, no. 6, 2014.
S. Bravyi et al., "Quantum self-correction in the 3d cubic code mode," Phys. Rev. Lett., vol. 111, no. 20, 2013.
G. Duclos-cianci et al., "Fault-tolerant renormalization group decoder for abelian topological codes," arXiv preprint, CoRR, 2013, arXiv: 1304.6100.
S. Varsamopoulos, "Neural network based decoders for the surface code," Ph.D. Thesis, Delft University of Technology, 2019.
A.J. Ferris et al., "Tensor networks and quantum error correction," Phys. Rev. Lett., vol. 113, 2014, article no. 030501.
A.J. Ferris and D. Poulin, "Branching MERA codes: A natural extension of classical and quantum polar codes," in Proc. IEEE Int. Symp. Inf. Theory, (Honolulu, HI, USA), June 2014, pp. 1081-1085.
C.T. Chubb, "General tensor network decoding of 2D Pauli codes," arXiv preprint, CoRR, 2021, arXiv: 2101.04125.
S. Varsamopoulos et al., "Decoding small surface codes with feedforward neural networks," Quantum Sci. Technol., vol. 3, 2017, article no. 015004.
G. Torlai et al., "Neural decoder for topological codes," Phys. Rev. Lett., vol. 119, 2017, article no. 030501.
S. Krastanov et al., "Deep neural network probabilistic decoder for stabilizer codes," Sci. Rep., vol. 7, 2017, article no. 11003.
C. Chamberland et al., "Deep neural decoders for near term fault-tolerant experiments," Quantum Sci. Technol., vol. 3, no. 4, 2018, article no. 044002.
P. Baireuther et al., "Neural network decoder for topological color codes with circuit level noise," New J. Phys., vol. 21, 2019, article no. 013003.
Y.H. Liu et al., "Neural belief-propagation decoders for quantum error-correcting codes," Phys. Rev. Lett., vol. 122, 2019, article no. 200501.
T. Wagner et al., "Symmetries for a high-level neural decoder on the toric code," Phys. Rev. A, vol. 102, 2020, article no. 042411.
S. Varona et al., "Determination of the semion code threshold using neural decoders," Phys. Rev. A, vol. 102, 2020, article no. 032411.
S. Gicev et al., "A scalable and fast articial neural network syndrome decoder for surface codes," arXiv preprint, CoRR, 2021, arXiv: 2110.05854.
H.P. Nautrup et al., "Optimizing quantum error correction codes with reinforcement learning," Quantum, vol. 3, 2019.
T. Fosel et al., "Reinforcement learning with neural networks for quantum feedback," Phys. Rev. X, vol. 8, 2018, article no. 031084.
P. Andreasson et al., "Quantum error correction for the toric code using deep reinforcement learning," Quantum, vol. 3, 2019.
D. Fitzek, "Error correction for depolarising noise on a quantum system using deep RL," Master’s Thesis at Chalmers University of Technology, 2019.
D. Fitzek et al., "Deep Q-learning decoder for depolarizing noise on the toric code," Phys. Rev. Research, vol. 2, 2020, article no. 023230.
L. Domingo Colomer et al., "Reinforcement learning for optimal error correction of toric codes," Phys. Lett. A, vol. 384, 2020, article no. 126353.
R. Sweke et al., "Reinforcement learning decoders for fault-tolerant quantum computation," arXiv preprint, CoRR, 2018, arXiv: 1810.07207.
D. Horgan et al., "Distributed prioritized experience replay," arXiv preprint, CoRR, 2018, arXiv: 1803.00933.
K. He et al., "Deep residual learning for image recognition," in Proc. IEEE CVPR 2016, (Las Vegas, NV, USA), June 2016, pp. 770-778.
R.S. Sutton et al., "Policy gradient methods for reinforcement learning with function approximation," in Advances in Neural Information Processing Systems, MIT Press, Cambridge, Massachusetts, USA, 2000, pp. 1057-1063.
J.R. Wootton et al., "High threshold error correction for the surface code," Phys. Rev. Lett., vol. 109, 2012, article no. 160503.
A. Hutter et al., "Efficient markov chain monte carlo algorithm for the surface code," Phys. Rev. A, vol. 89, 2014, article no. 022326.
F. Battistel et al., "Real-time decoding for fault-tolerant quantum computing: Progress, challenges and outlook," arXiv preprint, CoRR, 2023, arXiv: 2303.00054.
A. Holmes et al., "NISQ+: Boosting quantum computing power by approximating quantum error correction," in Proc. ACM/IEEE ISCA 2020, (Valencia, Spain), May 2020, pp. 556-569.
Y. Ueno et al., "QECOOL: On-line quantum error correction with a superconducting decoder for surface code," in Proc. ACM/IEEE DAC 2021, (San Francisco, CA, USA), Dec. 2021, pp. 451-456.
P. Das et al., "LILLIPUT: A lightweight low-latency lookup-table based decoder for near-term quantum error correction," in Proc. ASPLOS 2022, (Lausanne, Switzerland), Feb. 2021, pp. 541-553.
R.W.J. Overwater et al., "Neural-network decoders for quantum error correction using surface codes: A space exploration of the hardware cost-performance tradeoffs," IEEE Trans. Quantum Engineering, vol. 3, 2022, pp. 1-19.
P. Das et al., "AFS: Accurate, fast, and scalable error-decoding for fault-tolerant quantum computers," in Proc. IEEE HPCA 2022, (Seoul, Republic of Korea), Apr. 2022, pp. 259-273.
Y. Ueno et al., "QULATIS: A quantum error correction methodology toward lattice surgery," in Proc. IEEE HPCA 2022, (Seoul, Republic of Korea), Apr. 2022, pp. 274-287.
Y. Ueno et al., "NEO-QEC: Neural network enhanced online superconducting decoder for surface codes," arXiv preprint, CoRR, 2022, arXiv: 2208.05758.
G.S. Ravi et al., "Better than worst-case decoding for quantum error correction," in Proc. ASPLOS 2023, vol. 2, (Vancouver, Canada), Mar. 2023, pp. 88-102.
N. Liyanage et al., "Scalable quantum error correction for surface codes using FPGA," arXiv preprint, CoRR, 2023, arXiv: 2301.08419.
L. Skoric et al., "Parallel window decoding enables scalable fault tolerant quantum computation," arXiv preprint, CoRR, 2023, arXiv: 2209.08552.
표 1 오류 복호기의 주요 성능 지표
표 2 주요 복호화 알고리즘의 성능 지표 비교
| 알고리즘 | 정확성 | 저지연성 | 확장성 |
|---|---|---|---|
| LUT | 매우 높음 | 낮음 | 매우 낮음 |
| TN | 매우 높음 | 보통 | 보통 |
| MWPM | 높음~매우 높음 | 보통 | 보통 |
| UF | 높음 | 낮음 | 높음 |
| ML | 높음 | 낮음 | 보통 |
출처 Reproduced from [3].
표 3 주요 고전 방식 오류 복호화 알고리즘의 특징
| 사례 | 알고리즘 | 오류 임계값 | dmax | 계산 복잡도 |
|---|---|---|---|---|
| Caltech (2004) [6] | MWPM | 0.154 | 63 | O(n3)~O(d2.11) |
| Caltech/MS/ICL (2021) [7] | UF | 0.146 | 127 | O(n·α(n)), α(n)≤3 |
| UdeS (2010) [8] | RG | 0.164 | 128 | O(d2logd)~O(logd) |
| UdeS/ETHZ (2021) [9] | TN | 0.188 | 64 | O(nlogn + nχ3) |
표 4 신경망 기반 오류 복호기 연구 사례
| 사례 | 알고리즘 | 오류정정부호 | 노이즈 모델 | 오류 임계값 | dmax | 계산 복잡도 |
|---|---|---|---|---|---|---|
| TU Delft(2017) [22] | FFNN | Surface Code | 탈분극 | ~0.15 | 7 | O(MWPM) |
| Waterloo Univ.(2017) [23] | Restricted BM | Toric Code | i.i.d. 비트반전 | ~0.110 | 6 | > O(MWPM) |
| Yale Univ.(2017) [24] | FFNN | Toric Code | 탈분극 | 0.164 | 11 | >> O(MWPM) |
| Waterloo Univ.(2018) [25] | LSTM+3DCNN | Surface Code | 회로수준 | ~7.11×10 | 5 | N/A |
| Leiden Univ./TU Delft(2019) [26] | RNN/LSTM | Color Code | 회로수준 | ~0.0023 | 7 | N/A |
| UdeS(2019) [27] | BP | Toric Code | i.i.d. X&Z | ~0.07 | 10 | N/A |
| Dusseldorf Univ.(2019) [28] | FFNN(+MWPM) | Toric Code | 탈분극 | N/A | 7 | O(MWPM) |
| TU Delft(2020) [29] | DL+RG | Toric Code | i.i.d. 비트반전 | ~0.103 | 64 | > O(RG) |
| UCM(2020) [30] | MLP+CNN | Semion Code | 탈분극 | ~0.105 | 13 | N/A |
| Melbourne Univ.(2021) [31] | CNN(+HDRG) | Surface Code | 탈분극, 편향 | 0.138 | 1,025 | > O(HDRG) |
| Cologne Univ.(2021) [5] | ML(+UF/MWPM) | Toric Code | 탈분극 | 0.167 | 255 | O(UF) |
※ i.i.d.(독립적이고 동일하게 분산된 노이즈)
출처 Reproduced from [5], CC BY-NC-SA 4.0.
표 5 강화학습 기반 오류 복호기 연구 사례
| 사례 | 오류정정부호 | 노이즈 모델 | 오류 임계값 | dmax | 계산 복잡도 |
|---|---|---|---|---|---|
| Innsbruck Univ./Leiden Univ./Konstanz Univ./MS(2018) [32] | Surface Code | i.i.d. | N/A | 3, 5 | O(UF) |
| MPL(2018) [33] | Surface Code | 비트반전, 상관 노이즈 | N/A | N/A | N/A |
| Gothenburg Univ.(2019) [34] | Toric Code | i.i.d. 비트반전 | ~0.1 | 7 | >> O(n) (추정) |
| Chalmers Univ.(2019) [35] | Toric Code | 탈분극 | N/A | 5, 7 | > O(MWPM) |
| Chalmers Univ.(2020) [36] | Toric Code | 탈분극 | ~0.165 | 7(9) | >> O(n) (추정) |
| UAB(2020) [37] | Toric Code | i.i.d. 비트반전 | 0.103 | 9 | > O(MWPM) |
| FU Berlin/Copenhagen Univ.(2020) [38] | Surface Code | i.i.d. 비트반전 & 탈분극 | N/A | 5 | >> O(n) (추정) |
| Toulouse Univ./Copenhagen Univ.(2021) [39] | Toric Code | 비트반전 | N/A | 7(11) | > O(MWPM) |
※ i.i.d.(독립적이고 동일하게 분산된 노이즈)
표 6 주요 극저온 환경 하드웨어 복호기의 메트릭 비교
| 복호기 | NISQ+ [46] | PED+NN [49] | QULATIS [51] | NEO-QEC [52] | Clique [53] |
|---|---|---|---|---|---|
| 플랫폼 | SFQ | Cryo-CMOS | SFQ | SFQ | SFQ |
| 측정 오류 | - | - | ✓ | ✓ | ✓ |
| 격자 연산 | - | - | ✓ | ✓ | - |
| 면적(mm2) | 369 | 10 | 16.4 | N/A | 14.4 |
| 전력(µW) | 3,780 | 20,000 | 417.4 | 614.9 | 99 |
| 지연(ns) 최대/평균 | 19.2/3.8 | 28 | 82/2.12 | N/A | 0.24 |
※ 면적, 전력 소비 및 지연은 d=9 논리 큐비트 기준임.
CMOS: Complementary Metal-Oxide-Semiconductor
SFQ: Single Flux Quantum
출처 Reproduced from [45], CC BY 4.0.
표 7 하드웨어 기반 오류 복호기 연구 사례
| 사례 | 연구기관 | 특징 | 달성치 |
|---|---|---|---|
| NISQ+ [46] | Chicago Univ./USC(2020) | AQEC(Approximate QEC) 방법 / MWPM에 근사 / 확장성을 위한 SFQ 모듈의 2차원 배열 / 전력 절감을 위한 ERSFQ(Energy-efficient Rapid SFQ) 라이브러리 / (문제점) 리소스 병목 현상, 확장성 제약, 측정 오류 반영 미흡 | d=3, 5, 7, 9 / 평균 지연: 20ns / 최초 SFQ 칩 |
| QECOOL [47] | Tokyo Univ./NTT(2021) | 오류정정 주기 단축을 위한 3D 격자 기반의 온라인 QEC / 극저온 환경에서도 작동 / 2,500 논리 큐비트 / 오류 임계값을 소폭 낮춰 확장성 향상 / 면적 효율적인 소형 레지스터 기반 분산 구조 / NISQ+ 이상의 성능 달성(지연 지표는 제외) | d=5, 7, 9, 11, 13 / SFQ |
| LILLIPUT [48] | Google(2021) | 단기 양자 HW를 위한 실시간 복호화 / 가장 가능성이 높은 오류 이벤트 데이터만 저장하여 3레벨 압축 LUT(CLUT) 유지 / 백만 번의 무작위 시도를 통해 몬테카를로 시뮬레이션 인프라 검증 | d=3, 4, 5 / 평균 지연: 21ns (최대, ≤42ns) |
| PED+NN [49] | TU Delft(2022) | 저수준 PED 복호기와 고수준 FFNN 복호기로 2단계 신경망 복호기 구현 / 복호화 성능(오류율, 연산 지연)과 HW 비용(면적, 전력) 간의 절충 평가 / 모든 오류 체인 등거리 라우팅 최소화 및 회전 대칭성 활용으로 빠른 HW 복호화 달성 | d=3, 5, 7, 9 / 지연: ASIC (< 30ns), FPGA (< 90ns) 극저온 Cryo-CMOS |
| AFS [50] | Georgia Tech/Caltech/MS(2022) | 저장공간 및 대역폭 요구 스케일링과 관련한 도전 요인 분석 / 측정 오류 반영 / CDA(Conjoined Decoder Architecture)를 사용하여 저장소 부하 경감 / 희소 데이터 특성을 활용하여 신드롬 데이터 30배 압축 | d=11 / 평균 지연: 42ns, 99.9%의 지연: 150ns |
| QULATIS [51] | Tokyo Univ./NTT(2022) | 실용적인 복호화 회로로 격자 연산을 지원하는 온라인 QEC 알고리즘 / 병합 과 분할을 위해 유연한 경계 제어 / NISQ+ 및 QECOOL보다 향상된 확장성 / MWPM 복호기보다 낮은 성능 | d=5, 7, 9, 11 / SFQ & Cryo-CMOS |
| NEO-QEC [52] | Tokyo Univ./NTT(2022) | 합성곱신경망과 기존 온라인 그리드 복호기를 결합하여 측정 오차가 있는 표면 코드 및 격자 연산을 복호화하기 위한 신경망 기반 온라인 QEC 알고리즘 | d=5, 7, 9, 11, 13 / SFQ |
| Clique [53] | Chicago Univ./USC/IBM(2023) | SFQ 로직 극저온 도메인을 위한 경량 복호기 / 오프칩 복호화 대역폭(BW) 할당을 위한 통계적 신뢰도 기반 기법 / BTWC(Better Than Worst-Case) 복호화를 사용하여 70~99% 이상의 오프칩 대역폭 제거 / d=9에서 NISQ+ 대비 15~37배 자원 부하 경감 / 정확성과 처리 성능을 위한 온오프칩 2단계 분리 설계 | d=3, 5, 7, 9, 11 / SFQ |
| Helios [54] | Yale Univ. (2023) | 분산형 UF 복호기 / FPGA를 사용한 확장형 구조 / 병렬 컴퓨팅 자원을 하이브리드 트리-그리드 구조로 구성한 확장형 아키텍처 / 평균 10.7 주기 (AFS 168주기, QECOOL 41주기) | d = 7 (~ 15) / 평균 지연: 120ns |
- Sign Up
- 전자통신동향분석 이메일 전자저널 구독을 원하시는 경우 정확한 이메일 주소를 입력하시기 바랍니다.